|
|
|||
|
БІОСИСТЕМИ. БІОСФЕРА
ЕКОСИСТЕМИ. ПОПУЛЯЦІЇ
ОРГАНІЗМИ У ДОВКІЛЛІ
ЛЮДСТВО ТА ЙОГО ДОЛЯ
|
|||
|
← IV-4. Експоненційне і логістичне зростання чисельності популяції |
IV-5. Модель Лотки-Вольтерра |
||
IV-5. Модель Лотки-Вольтерра
У 1925 році відомий італійський математик Віто Вольтерра, розмовляючи за обідом зі своїм майбутнім зятем, іхтіологом за фахом, зацікавився популяційною динамікою риб. Зокрема він дізнався, що зниження вилову риби під час першої світової війни призвело до збільшення частки хижої риби в уловах. Результатом осмислення таких фактів стали запропоновані ним моделі для опису міжвидової взаємодії.
«Системи, вивчені Вольтерра, складаються з декількох біологічних видів і запасу їжі, який використовують деякі з розглянутих видів. Про компоненти системи формулюються такі припущення.
1. Їжа або є у необмеженій кількості, або її надходження з плином часу жорстко регламентоване.
2. Особини кожного виду відмирають таким чином, що за одиницю часу гине постійна частка існуючих особин.
3. Хижі види поїдають жертви, причому за одиницю часу кількість з'їдених жертв завжди пропорційна ймовірності зустрічі особин цих двох видів, тобто добутку кількості хижаків на кількість жертв.
4. Якщо є їжа у необмеженій кількості та є кілька видів, які здатні її споживати, то частка їжі, споживана кожним видом за одиницю часу, пропорційна кількості особин цього виду, взятого з деяким коефіцієнтом, що залежить від виду (моделі міжвидової конкуренції).
5. Якщо вид харчується їжею, наявною у необмеженій кількості, приріст чисельності виду за одиницю часу пропорційний чисельності виду.
6. Якщо вид харчується їжею, наявною в обмеженій кількості, то його розмноження регулюється швидкістю споживання їжі, тобто за одиницю часу приріст пропорційний кількості з'їденої їжі.
Перераховані гіпотези дозволяють описувати складні живі системи за допомогою систем звичайних диференціальних рівнянь» (Г.Ю. Різниченко, 1999).
За своєю суттю моделі Вольтерра виявилися близькі до моделі, яку А. Лотка запропонував в 1925 році для опису кінетики ланцюгових хімічних реакцій (де продукт однієї реакції служить субстратом для наступної).
У нашому підручнику ми викладемо модель Лотки-Вольтерра у тій її формі, в якій вона розвиває логістичну модель. Розглянемо, наприклад, два види, А і В, які є конкурентами й використовують один і той же ресурс. Наведемо динаміку цих видів за допомогою логістичних рівнянь, але врахуємо в них як обмеження ємності середовища, пов'язані з вилученням ресурсів особинами свого виду, так і аналогічний вплив з боку особин чужого виду.
Що показує співмножник у правій частині логістичного рівняння: (K-N) / K? Що в міру зростання чисельності (N) для популяції залишається доступною все менша частина ємності середовища (K). Але якщо доступні ресурси забирають не тільки особини одного виду, але й особини виду-конкурента, цей ефект теж можна врахувати в моделі, ввівши в рівняння для виду А елементи, що описують вплив виду В. Однак вид В перебуває в аналогічному становищі – частину його ресурсів забирають особини виду А!
Оскільки види відрізняються один від одного, кількість ресурсів, що вилучаються їх особинами, буде різною. Введемо коефіцієнт β, який показує, скільки особин виду В споживає ту ж кількість ресурсів, що й одна особина виду А. Аналогічно введемо коефіцієнт α, який покаже, скільки особин виду А споживає таку ж кількість ресурсів, як і одна особина виду В. Тоді, позначаючи підрядковими символами А і В значення відповідних величин для двох видів, можна написати систему з двох взаємопов'язаних рівнянь.
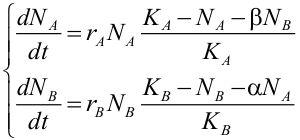
Модель Лотки-Вольтерра зіграла виняткову роль у розвитку математичної екології. Як легко зрозуміти, на її основі можна побудувати безліч інших, складніших моделей. Наприклад, вони можуть описувати взаємозв'язок не двох, а більшої кількості ресурсів. Параметр K для кожного з видів може бути незмінним, а може змінюватися за якимсь законом (наприклад, залежно від зміни погоди або зміни пори року). Реакція одного виду на зміну чисельності іншого може відбуватися з більшою або меншою затримкою тощо. Наведені тут нескладні рівняння – досить потужний інструмент для дослідження природних процесів!
