|
|
|||
|
БІОСИСТЕМИ. БІОСФЕРА
ЕКОСИСТЕМИ. ПОПУЛЯЦІЇ
ОРГАНІЗМИ У ДОВКІЛЛІ
ЛЮДСТВО ТА ЙОГО ДОЛЯ
|
|||
|
I-8. Стійкість біосистем |
I-9. Моделювання як пізнання — і біосистем, і усього іншого → |
||
I-8. Стійкість біосистем
Життя подібне до їзди на велосипеді. Щоб тримати рівновагу, слід безперервно рухатися.
Альберт Ейнштейн
Характерна особливість регуляції за принципом негативного зворотного зв'язку полягає в тому, що вона призводить до коливань регульованої величини. Цікаво порівняти, наприклад, явища, що відбуваються в столі, що стоїть, і в тілі людини, яка стоїть поряд. Стіл зазнав пружної деформації, при якому дія сили тяжіння врівноважилася силою пружності, і перебуває в нерухомості. Людина безперервно контролює свою позу (використовуючи для цього значну частину «потужності» свого мозку). Невелике відхилення тіла в одну зі сторін викликає спрацьовування рецепторів, які підключають ефектори (м'язи), що повертають систему в необхідний стан. Дія цих ефекторів компенсує відхилення з певним надлишком. Через це система проходить через оптимальний стан і потребує регуляторного впливу у зворотному напрямку. Тіло людини, що стоїть, виявляється залученим одночасно в кілька коливальних процесів з різною частотою та амплітудою! Саме тому людина, що стоїть, втомлюється і витрачає енергію, а стіл не витрачає енергії та не зношується.
А що станеться, якщо біосистема, стан якої регулюється за принципом негативного зворотного зв'язку, зазнає якогось зовнішнього впливу, що змінить її параметри? Розглянемо це на прикладі регуляції чисельності популяції. Популяція, що знаходиться в стійкому стані, зберігає свою чисельність відносно постійною, відчуваючи при цьому безперервні коливання. Припустимо, катастрофічні події або вплив людини знищили значну частину особин. Як популяція відреагує на цей вплив?
Якщо вплив виведе популяцію за межі регулювання її чисельності негативними зворотними зв'язками, вона перейде в інший стан (наприклад, загине; рис. I-8.1). Так, якщо чисельність особин у ній стане дуже низькою, може порушитися їх розмноження (наприклад, через те, що партнери не зможуть знайти один одного). Спрацюють позитивні зворотні зв'язки: зниження чисельності популяції викличе зниження народження нових особин. В результаті біосистема перейде в інший стан (популяція загине). Якщо ж вплив виявиться не критичним, негативні зворотні зв'язки зможуть повернути чисельність популяції до норми. Це означає, що зниження чисельності викличе ослаблення внутрішньовидової конкуренції, посилення розмноження і краще виживання молоді.
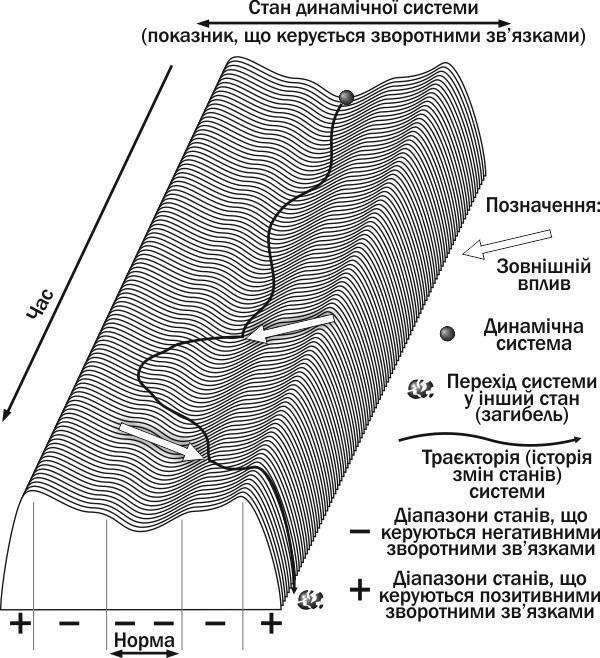
Рис. I-8.1. Траєкторія системи, керованої зворотними зв'язками. Перший зовнішній вплив вивів систему з діапазону норми, але більш потужні негативні зв'язки повернули її в діапазон норми. Другий зовнішній вплив перевів систему в діапазон дії позитивних зворотних зв'язків, які посилили відхилення і привели систему до загибелі
Для опису процесів, аналогічних тим, які були згадані вище (і тим, які показані на рис. I-8.1), важливо поняття стійкості. Проаналізуємо рис. I-08.1. Чи є стійким стан біосистеми, що перебуває в діапазоні норми? Так, причому для цього стану характерне те, що відхилення від рівноваги викликає дію механізмів, які повертають біосистему назад. Цій стійкості не заважає те, що розглянута біосистема знаходиться в стані безперервних змін.
У результаті зовнішніх впливів біосистема, динаміка якої показана на рис. I-8.1, загинула. Чи є стан загибелі стійким? Так, але це інша стійкість, ніж у випадку норми. Стан системи, що перебуває на «гребені», що розділяє діапазони станів, керованих негативними та позитивними зворотними зв'язками (а також системи, що «скочується» під впливом позитивних зворотних зв'язків), можна назвати нестійким. Це означає, що з погляду стійкості ці стани відносяться до особливих типів.
Отже, для подальшого обговорення необхідно визначити поняття «стійкість». Воно стало одним з найважливіших екологічних понять з ранніх етапів розвитку екології. Приміром, воно було ключовим для теорії клімаксу рослинних угруповань Ф. Клементса, що з'явилася на початку XX століття.
Стійкість рослинного угруповання — його здатність «зберігати свій склад і лад протягом тривалого часу. Ця стійкість обумовлена здатністю угруповання до самовідтворення» (В. М. Сукачов).
Використання поняття «стійкість» в екології — окремий випадок його загальнонаукового вживання. Класичним визначенням поняття «стійкість» є те, яке було дано в 1892 р. творцем теорії стійкості руху Олександром Михайловичем Ляпуновим (доцентом, а пізніше — професором Харківського університету, що нині названий на честь В. Н. Каразіна). Стійкість визначалася О. М. Ляпуновим з погляду впливів збурень на рух з певними початковими умовами. Застосування такого підходу до опису динаміки біосистем стикається зі значними складнощами й не цілком відповідає традиції, що склалася в екології. На нашу думку, з математичних підходів для екології корисніше всього уявлення про сталість за Ж. Л. Лагранжем, яке є окремим випадком стійкості за О. М. Ляпуновим. З цього погляду, стійкість є здатністю системи залишатися в обмеженій області свого фазового простору.
Фазовим простором в цьому випадку називається сукупність можливих станів системи, описаних за допомогою набору її змінних стану (наприклад, переміщення системи у фазовому просторі показано на рис. I-8.1). Вибір змінних, які задають фазовий простір, дозволяє, наприклад, розглядати стійкість угруповання і з погляду числа його видів, і з погляду сталості його структури. Суть феномена стійкості залишається при цьому незмінною, змінюється лише набір координат, в якому досліджується траєкторія системи.
А чим обмежена певна область фазового простору? Траєкторіями систем, що знаходяться в цій області. На рис. I-8.1. можна побачити певні обмежені області фазового простору: зону стійкої рівноваги, в якій стан системи управляється негативними зворотними зв'язками, і дві зони (праворуч і ліворуч від зони стійкої рівноваги), в яких динаміку системи визначають позитивні зворотні зв'язки. Особливим станом є, ймовірно, положення на «гребені», що розділяє області «+» і «—» управління, а також стан загиблої системи. Ці області фазового простору можна назвати басейнами стійкості. Кожному басейну стійкості відповідає свій динамічний тип розглянутих біосистем (поняття динамічного типу докладніше аналізується в пункті I-12).
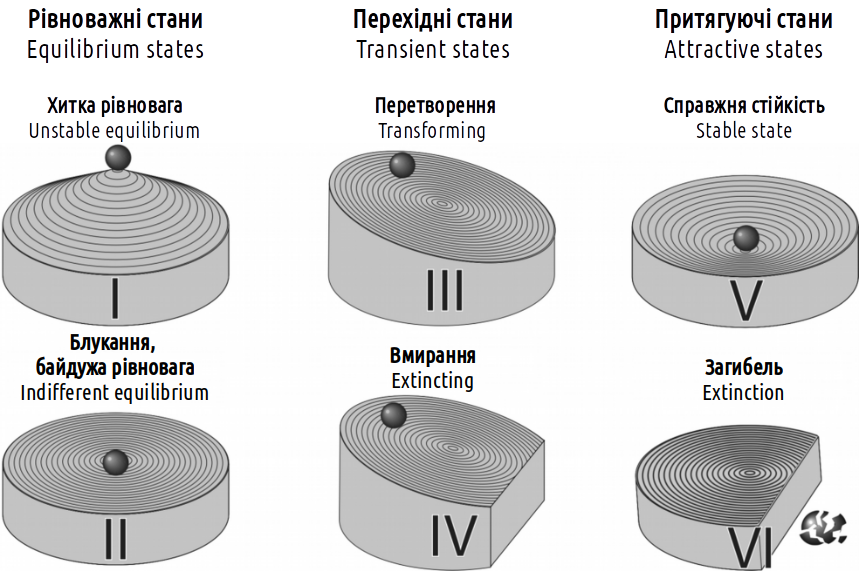
Авторами даного посібника за результатами вивчення зміни складу геміклональних популяційних систем гібридогенного комплексу зелених жаб запропонована класифікація типів стійкості біосистем, показана (за допомогою фізичних аналогій) на рис. I-8.2. Можна припустити, що ця класифікація застосовна не тільки для вивченої категорії систем, а й для будь-яких інших.
Рис. I-8.2. Класифікація типів стійкості систем
Різниця між фізичними аналогіями, використаними на рис. I-8.1 і I-8.2 пов'язана з тим, що на першому малюнку характер профілю поверхні (що визначає характерну для певного типу стійкості динаміку системи) показаний в одній площині, а на другому — у двох перпендикулярних площинах. Аналізуючи динаміку системи на рис. I-8.1, можна знайти всі показані на рис. I-8.2 типи стійкості, за винятком типу II (блукання). Цей випадок відповідає ситуації, коли зміна стану системи виявляється байдужою для дії механізмів, що керують її динамікою. Типу I (хиткій рівновазі) відповідає положення на «гребені», що розділяє діапазони регуляції негативними та позитивними зворотними зв'язками. Відхилення системи від стану хиткої рівноваги призведе до її переходу в один з альтернативних станів.
Слід підкреслити, що в більшості випадків автори, які пишуть про стійкість систем, мають на увазі саме стани їх справжньої стійкості (тип V за наведеною класифікацією). Природно, у багатьох випадках саме такі стани становлять найбільший інтерес. Приміром, завдання охорони тієї чи іншої біосистеми (наприклад, цінної екосистеми на заповідній території) може бути представлена як задача її підтримки в V типі стійкості. Характерною особливістю цього стану є те, що у разі відхилення від рівноважного стану виникає сила, що повертає систему в тій самий рівноважний стан.
Динаміка зміни показників системи, що перебуває в стані стійкості IV типу, становить значний інтерес для її діагностики (і прогнозу її майбутніх змін). Те, з якою швидкістю змінена система повернеться у свій нормальний стан, є її важливою характеристикою. Аналізуючи її динаміку, можна виділити два відносно незалежні параметри: здатність протистояти дії та здатність повертатися в норму після зміни. Ці параметри відбивають різні властивості системи (їх можна порівняти з твердістю і пружністю в механіці: алмаз твердий, але не пружний, а гума не тверда, але пружна). Ці параметри пов'язані негативною кореляцією (як і міцність і пружність в класичній механіці). Вони є двома складниками загальної стійкості (показаної на рис. I-8.3 у вигляді площі між кривою, яка описує динаміку стану системи, і «коридором» норми).
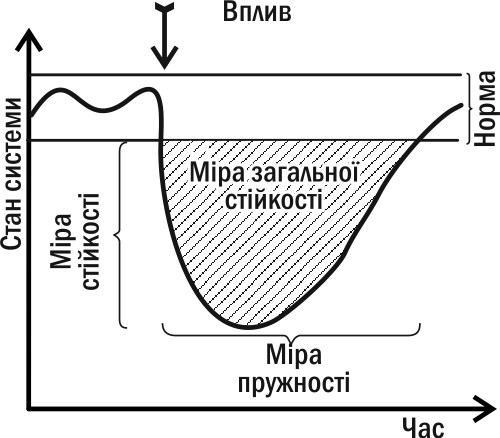
Рис. I-8.3. Основні міри стійкості, застосовні для біосистем, що знаходяться в стані стійкості IV типу (див. рис. I-8.2)