|
||||
|
← |
Д.А. Шабанов, М.А.Кравченко. Статистический анализ данных в зоологии и экологии |
→ |
||
|
Тема 5 (продолжение). Многофакторный дисперсионный анализ |
||||
|
Биостатистика-08 |
Биостатистика-10 |
|||
5.6. Два однофакторных дисперсионных анализа: вычисление «вручную»
Как и в случае однофакторного анализа, обработаем простой пример, содержащий данные со специально подобранными цифрами. Это результаты тестирования студентов мужского и женского пола по трем тестам: «легкому», «среднему» и «сложному». Данные расположены не случайно, а сгруппированы по полу, сложности теста, а внутри этих групп — по возрастанию полученного балла.
|
Sex |
Test |
Balls |
|
Sex |
Test |
Balls |
|
Sex |
Test |
Balls |
|
Female |
Light |
64 |
Female |
Hard |
10 |
Male |
Medium |
43 |
||
|
Female |
Light |
69 |
Female |
Hard |
25 |
Male |
Medium |
45 |
||
|
Female |
Light |
73 |
Female |
Hard |
34 |
Male |
Medium |
65 |
||
|
Female |
Light |
90 |
Female |
Hard |
41 |
Male |
Medium |
71 |
||
|
Female |
Light |
94 |
Female |
Hard |
60 |
Male |
Medium |
96 |
||
|
Female |
Medium |
30 |
Male |
Light |
41 |
Male |
Hard |
34 |
||
|
Female |
Medium |
39 |
Male |
Light |
43 |
Male |
Hard |
41 |
||
|
Female |
Medium |
63 |
Male |
Light |
53 |
Male |
Hard |
60 |
||
|
Female |
Medium |
72 |
Male |
Light |
65 |
Male |
Hard |
64 |
||
|
Female |
Medium |
76 |
Male |
Light |
78 |
Male |
Hard |
71 |
Итак, в каждой группе содержится по 5 результатов, всего в файле 6 групп. Фактически, по приведенным данным можно провести два однофакторных анализа: по влиянию пола испытуемых и по влиянию сложности тестов.
Сказанное означает, что мы можем вычислить суммы квадратов и средние квадратов как в целом для всех результатов, так и для двух способов подразделений: на две группы по полу и на три группы по сложности.
Первый однофакторный анализ
Вычислим общую сумму квадратов.  = 57, SS = (64–57)2 + (69–57)2 + …=12742.
= 57, SS = (64–57)2 + (69–57)2 + …=12742.
Для вычисления этой величины без использования ANOVA, но с применением пакета Statistica, а не на калькуляторе или на счетах, можно сделать следующее. В содержащем обсуждаемые данные файле создается (Vars / Add) еще один столбец, например, расположенный после столбца Balls. Двойной щелчок на заголовке (верхней клеточке с названием) этого столбца или выбор режима Vars / Specs приводит в окно управления свойствами этого столбца. В расположенном снизу окошке Long name (label or formula) вписываем (без кавычек) «=(Balls-57)**2». Вместо названия столбца «Balls» можно было просто указать номер столбца, например, «v3» («v» - принятое в данном случае сокращение от слова variables, а «3» - номер этого столбца в файле). Символ «**» означает возведение в степень; можно вместо него использовать также символ ^ (6 + Shift в английской раскладке клавиатуры). При выходе из режима редактирования заголовка столбца, программа переспросит, пересчитать ли его данные и заполнит его значениями квадратов отклонений от среднего. Для последующих пересчетов столбца можно использовать команду Vars/Recalculate Spreadsheet Formulas (или попросту Shift+F9).
Рис. 5.6.1. Описанный в тексте способ упрощения расчетов
Остается лишь определить сумму значений вычисленных квадратов отклонений. Это можно сделать при помощи режима вычисления описательных статистик: Statistics / Basic Statistics and Tables / Descriptive Statistics; во вкладке Advanced поставить флажок напротив параметра Sum и провести вычисления. Есть и более простой способ: выделить столбец мышью, щелкнуть на выделенном поле правой клавишей, а затем выбрать Statistics of Block Data / Block Columns / Sum. В файле появится еще одна строка, в которую будет автоматически вставлено соответствующее значение.
Рис. 5.6.2. Быстрый способ вычислений с использованием меню Statistics of Block Data, который вызывается щелчком правой клавиши мыши
Аналогичным образом определим средние суммы квадратов для женщин и мужчин (при этом в столбец файла для вычисления квадратов разности средних нужно вставлять соответствующие значения групповых средних, а потом суммировать их в блоках, охватывающих требуемые группы).
 F = 56, SSF = (64–56)2 + (69–56)2 + …=8594;
F = 56, SSF = (64–56)2 + (69–56)2 + …=8594;  M = 58, SSМ = (41–58)2 + (43–58)2 + …=4118.
M = 58, SSМ = (41–58)2 + (43–58)2 + …=4118.
Суммируя полученные величины, мы получим SSошибки(S) (значок «S» означает, что мы говорим об ошибке при разделении совокупности по признаку «Sex»).
SSошибки(S) = SSF + SSМ = 8594 + 4118 = 12712. Число степеней свободы для этой величины dfошибки(S) = 30 — 2 = 28 (тридцать оценок и два уравнения, которые связывают две их группы).
MSошибки(S) = SSошибки(S) / dfошибки(S) = 12712/28 = 454.
Вычисляем MSэффекта(S). SSэффекта(S) = nF × ( F –
F –  )2 + nM × (
)2 + nM × ( M –
M –  )2 = 15 × 1 + 15 × 1 = 30.
)2 = 15 × 1 + 15 × 1 = 30.
dfэффекта(S) = 1. MSэффекта(S) = 30.
Мы получили средние квадраты для эффекта влияния пола и его ошибки. Если в сравнении по критериям Стьюдента и Фишера при вычислении критерия Фишера большая варианса делится на меньшую, в данном случае надо поступать иначе. Чтобы проверить статистическую значимость разделения всей совокупности по интересующему нас признаку, мы должны разделить средний квадрат эффекта на средний квадрат ошибки. Результат красноречивый:
F = MSэффекта(S) / MSошибки(S) = 30/454 = 0,061.
Статистическую значимость такого результата по таблицам можно не проверять. ANOVA утверждает, что вероятность разницы средних, не превышающей зарегистрированную, при случайном разделении их совокупности на части (т.е. величина p) равна 0,799. Итак, при однофакторном анализе мы зарегистрировали, что зависимость всей совокупности оценок от пола испытуемых несущественна. Впрочем (забегая вперед), двухфакторный анализ может существенно откорректировать это утверждение.
Второй однофакторный анализ
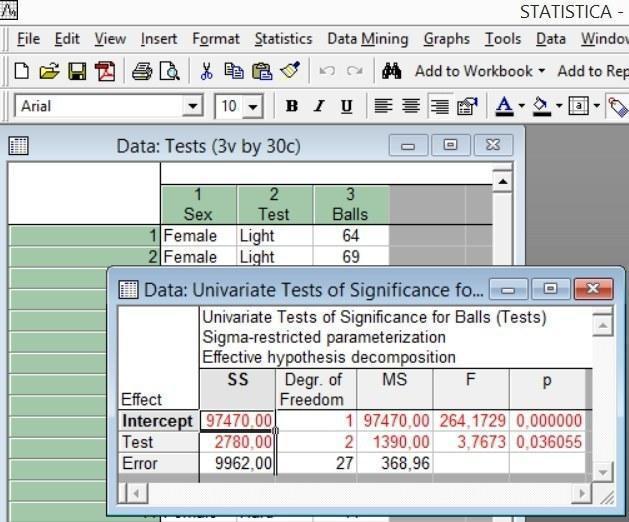
Однофакторный анализ, связанный с влиянием сложности тестов, проведем с использованием процедуры ANOVA в пакете Statistica, ведь в «ручных» вычислениях мы уже успели разобраться. Вот его результат (не обращаем внимания на строку Intercept!).
Рис. 5.6.3. Результат определения влияния сложности тестов на результат тестирования
Как видно, сложность тестов статистически значимо влияет на их результат. Поскольку 30 имеющихся оценок разбивалось на три группы, число степеней свободы для ошибки составляет 27.
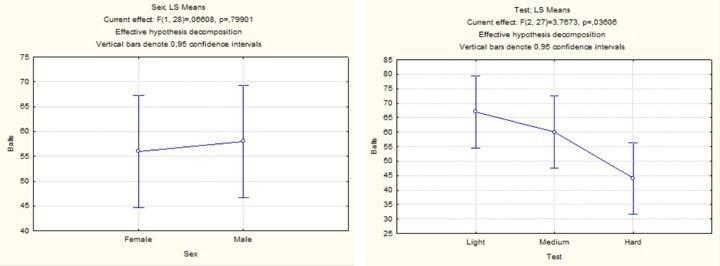
Итак, два однофакторных анализа показали, что влияние одного из факторов статистически незначимо, а второго — статистически значимо. На соответствующих графиках этот результат виден достаточно отчетливо.
Рис. 5.6.4. Графическое отображение результатов двух однофакторных анализов (по отдельности)
Интересно, что сравнение результатов тестов с помощью критериев Стьюдента и Фишера для пар Light — Medium и Medium — Hard показывает статистически незначимое отличие, и только для пары Light — Hard результат оказывается статистически значимым.
Но в обоих примененных нами анализах мы использовали не все имеющиеся данные. Мы разбивали данные на две и на три группы, а в нашем файле их 6! Двухфакторный анализ позволяет вскрыть новые обстоятельства.
5.7. Двухфакторный дисперсионный анализ: вычисление «вручную»
В однофакторных анализах мы использовали две модели для объяснения изменчивости оценки по тестам.
Связанную с влиянием пола модель можно представить так:  , где xis — i-тое значение изучаемой величины при s-том значении изучаемого фактора Sex;
, где xis — i-тое значение изучаемой величины при s-том значении изучаемого фактора Sex;  — общее среднее; Ss — влияние s-того значения фактора Sex;
— общее среднее; Ss — влияние s-того значения фактора Sex; 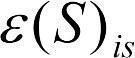 — «ошибка», вклад индивидуальности объекта при группировании по значениям указанного фактора.
— «ошибка», вклад индивидуальности объекта при группировании по значениям указанного фактора.
Аналогично можно было представить и вторую модель: 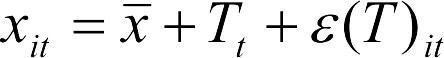 .
.
Как объединить эти модели? В значение «ошибки» в первом уравнении (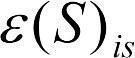 ) входит как индивидуальность, так и влияние сложности теста; аналогично «ошибка»
) входит как индивидуальность, так и влияние сложности теста; аналогично «ошибка» 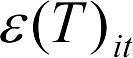 включает влияние пола испытуемых. Рассматривая среднее значение полученного представителями каждого пола результата, мы можем выделить часть ошибки, связанную со сложностью теста; при анализе ответа на тесты разной сложности можно выделить вклад пола в изменение результата.
включает влияние пола испытуемых. Рассматривая среднее значение полученного представителями каждого пола результата, мы можем выделить часть ошибки, связанную со сложностью теста; при анализе ответа на тесты разной сложности можно выделить вклад пола в изменение результата.
В целом можно написать 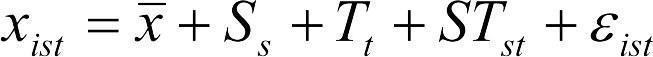 , где xist — i-тое значение изучаемой величины при s-том значении изучаемого фактора Sex и t-том значении изучаемого фактора Test, а STst — результат взаимодействия факторов Sex и Test при s-том и t-том их значении. Значит, мы можем использовать следующее разложение суммы квадратов на компоненты: SS = SSS + SST + SSST +SSошибки. Выполняя однофакторные анализы, мы уже установили, что SS = 12712, SSS = 30 и SST =2780. Суммы квадратов ошибок, которые мы вычисляли перед этим, отличаются от той, которая должна быть получена для двухфакторного анализа, ведь теперь ее надо вычислять для 6 групп. Не обсуждая процесс ее вычисления, ставший при условии понимания предшествовавших рассуждений тривиальным, укажем, что SSошибки = 7592. А как вычислить SSST?
, где xist — i-тое значение изучаемой величины при s-том значении изучаемого фактора Sex и t-том значении изучаемого фактора Test, а STst — результат взаимодействия факторов Sex и Test при s-том и t-том их значении. Значит, мы можем использовать следующее разложение суммы квадратов на компоненты: SS = SSS + SST + SSST +SSошибки. Выполняя однофакторные анализы, мы уже установили, что SS = 12712, SSS = 30 и SST =2780. Суммы квадратов ошибок, которые мы вычисляли перед этим, отличаются от той, которая должна быть получена для двухфакторного анализа, ведь теперь ее надо вычислять для 6 групп. Не обсуждая процесс ее вычисления, ставший при условии понимания предшествовавших рассуждений тривиальным, укажем, что SSошибки = 7592. А как вычислить SSST?
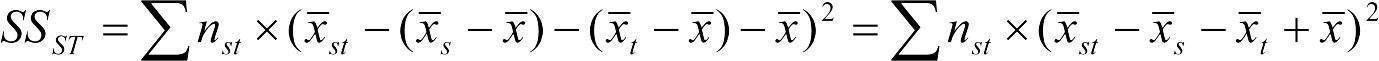 . В этой формулой символом «s» обозначены градации фактора S — Sex (принимающего 2 значения), а символом «t» — три градации фактора T — Test. В приложении к рассматриваемому случаю можно написать:
. В этой формулой символом «s» обозначены градации фактора S — Sex (принимающего 2 значения), а символом «t» — три градации фактора T — Test. В приложении к рассматриваемому случаю можно написать:
SSST = nFemaleLight × ( FemaleLight –
FemaleLight –  Female –
Female –  Light +
Light +  )2 + nFemaleMedium × (
)2 + nFemaleMedium × ( FemaleMedium –
FemaleMedium –  Female –
Female –  Medium +
Medium +  )2 + nFemaleHard × (
)2 + nFemaleHard × ( FemaleHard –
FemaleHard –  Female –
Female –  Hard +
Hard +  )2 + nMaleLight × (
)2 + nMaleLight × ( MaleLight –
MaleLight –  Male –
Male –  Light +
Light +  )2 + nMaleMedium × (
)2 + nMaleMedium × ( MaleMedium –
MaleMedium –  Male –
Male –  Medium +
Medium +  )2 + nMaleHard × (
)2 + nMaleHard × ( MaleHard –
MaleHard –  Male –
Male –  Hard +
Hard +  )2
)2
Приведем список групповых средних.  FemaleLight = 78;
FemaleLight = 78;  FemaleMedium = 56;
FemaleMedium = 56;  FemaleHard = 34;
FemaleHard = 34;  MaleLight = 56;
MaleLight = 56;  MaleMedium = 64;
MaleMedium = 64;  MaleHard = 54. Кроме того,
MaleHard = 54. Кроме того,  Female = 56;
Female = 56;  Male = 58, а также
Male = 58, а также  Light = 67;
Light = 67;  Medium = 60;
Medium = 60;  Hard = 44. Наконец,
Hard = 44. Наконец,  = 57. Для всех групп n = 5.
= 57. Для всех групп n = 5.
SSST=5×(78–56–67+57)2 + 5×(56–56–60+57)2 + 5×(34–56–44+57)2 + 5×(56–58–67+57)2 + 5×(64–58–60+57)2 + 5×(54–58–44+57)2.= 5×[122 + 32 + 92 + 122 + 32 + 92] = 2340.
Интерпретировать полученные результаты будет проще с помощью ANOVA в пакете Statistica, но зато теперь мы будем понимать, откуда взялись значения SS, MS и F, приведенные в результатах анализа.
5.8. Двухфакторный анализ с помощью ANOVA в пакете Statistica
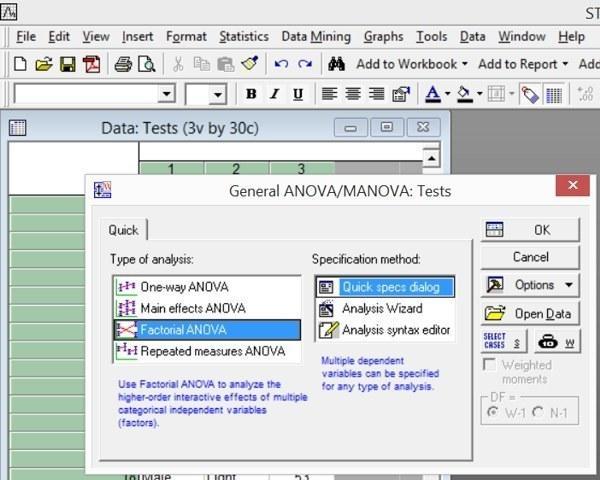
Открыв описанный файл в пакете Statistica, выберем вид анализа Statistics / ANOVA. В диалоге Quick в окне Type of analysis укажем Factorial ANOVA, а в окне Specification method укажем Quick specs dialog.
Рис. 5.8.1. Стартовое окно для проведения многофакторного анализа
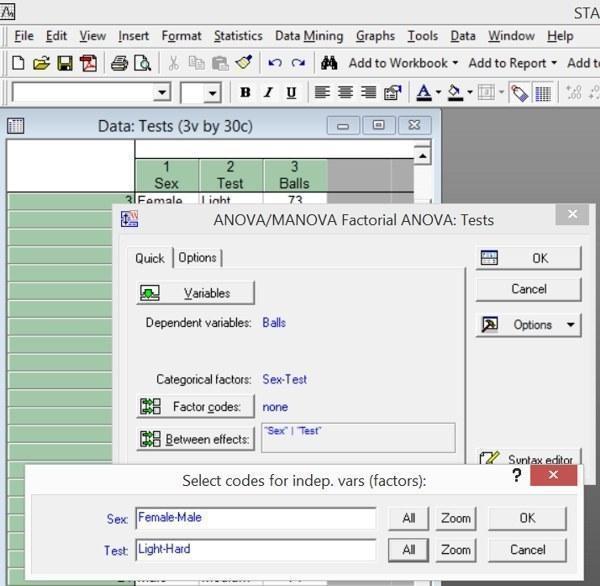
Нажав OK, попадаем в следующий диалог. Во вкладке Quick необходимо указать столбцы с факторами и исследуемыми признаками, а также необходимые коды факторов. Нажав кнопку Variables, в окне Dependent variables list укажем столбец Balls, а в окне Categorical predictors (factor) — столбцы Sex и Test (в этом и подобном окнах, если нужно выбрать несколько переменных, их можно выделять при щелчком мыши на их названии при нажатой клавише Contral). Жмем OK. В диалоге Factor codes для обоих факторов выбираем All.
Рис. 5.8.2. Выбор кодов факторов (значений переменных Sex и Test, для которых будет віполняться анализ). В обоих случаях нажаты кнопки All
Очередное OK переводит в окно ANOVA Results 1. Кнопка All effects выводит таблицу дисперсионного анализа.
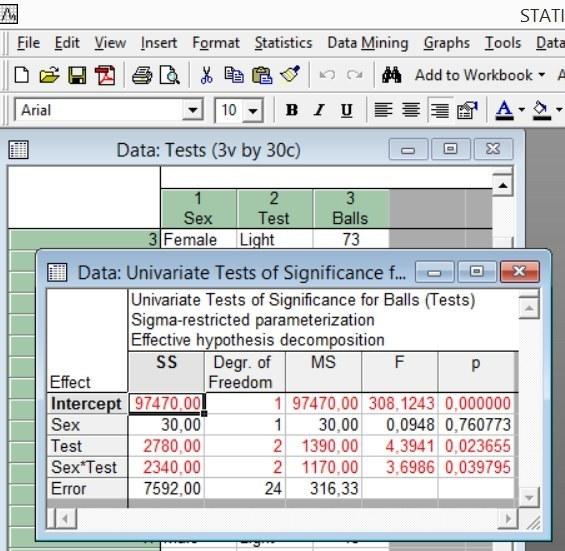
Рис. 5.8.3. Основная таблица результатов двухфакторного анализа
Как видно из таблицы, влияние признака Sex статистически незначимо, но и влияние признака Test, и взаимодействие Sex*Test оказывается статистически значимым. Чтобы понять, в чем заключается такое взаимодействие, полезно построить график с помощью кнопки All effects / Graphs в окне ANOVA Results 1. В открывающемся диалоге выбираем строку Sex*Test. Программа предлагает два варианта построения графика: с отображением на оси абсцисс признака Test или признака Sex. Приведем оба варианта.
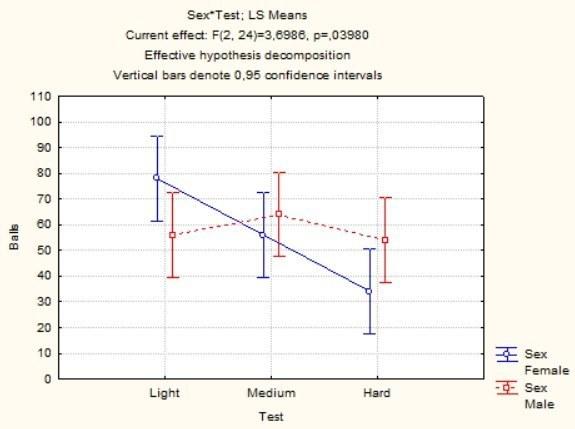
Рис. 5.8.4. Вариант графика, отражающего взаимодействие факторов, в котором на оси абсцисс показан признак Test, а точки, соответствующие определенным значениям признака Sex, показаны линиями
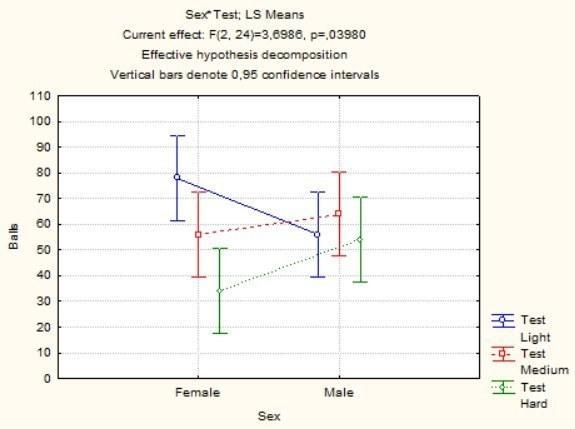
Рис. 5.8.5. Вариант графика, отражающего взаимодействие факторов, в котором на оси абсцисс показан признак Sex, а точки, соответствующие определенным значениям признака Test, показаны линиями
Очевидно, что проще работать с первым из графиков. Линиями на нем показаны результаты испытуемых двух полов. Мы видим, что с усложнением тестов женщины получают все меньшие баллы. Реакция мужчин на усложнение совсем другая: легкие тесты они решают неважно (может, просто от скуки), на тестах средней сложности повышают результат, а сложные тесты решают лишь ненамного хуже, чем легкие (возможно, воспринимают их как интеллектуальный вызов и поэтому серьезно напрягаются).
Итак, вывод, что пол не влияет на результаты тестов, нуждается в корректировке. Нет оснований утверждать, что один пол справляется с тестами хуже или лучше, чем другой; зато ясно, что мужчины реагируют на усложнение тестов совсем иначе, чем женщины. Значит, пол все-таки влияет на баллы, но не повышая или понижая оценку, а меняя реакцию на изменение другого фактора.
В возможности исследований такого рода эффектов взаимодействия факторов и проявляется одно из основных преимуществ дисперсионного анализа.