 |
||||
|
← |
Д.А. Шабанов, М.А.Кравченко. Статистический анализ данных в зоологии и экологии |
→ |
||
|
|
Содержание курса. |
|||
|
|
Биостатистика-02 |
|||
Содержание
Тема 1. Основные понятия биостатистики
1.1. Что такое биостатистика и зачем она нужна
1.2. Вероятность
1.3. Генеральная совокупность и выборка
1.4. Что такое значимость? Шуточный пример
1.5. Статистическая значимость; нулевая и альтернативная гипотезы
1.6. Признаки
1.7. Распределения, статистики и параметры
1.8. Параметрические и непараметрические статистические методы и критерии
Тема 2. Использование программы Statistica
2.1. Почему именно Statistica?
2.2. Программа Statistica
2.3. Структура таблицы данных Statistica
2.4. Действия с выделенными ячейками
2.5. Работа со строками и столбцами
2.6. Спецификации переменных
2.7. Числовая и текстовая формы данных
2.8. Формулы для пересчета данных
Тема 3. Визуализация данных (на примере результатов описания зеленых лягушек)
3.1. Описание файла-примера Pelophylax_example.sta
3.2. Гистограммы: пример построения графиков
3.3. Редактирование графика
3.4. Диаграммы рассеяния и линии регрессии
Тема 4. Сравнение выборок
4.1. В каких ситуациях может понадобиться сравнивать выборки?
4.2. Сравнение выборок по Стьюденту
4.3. Использование критерия Фишера для сравнения выборок
4.4. Диаграммы размаха в модуле t-теста
4.5. Проблема множественных сравнений
4.6. Эксперимент с получением ложно "значимых" отличий при множественных сравнениях
4.7. Поправки на множественные сравнения
4.8. Непараметрические аналоги параметрических методов
4.9. U-критерий Манна-Уитни
4.10. Критерий знаков для парных сравнений
4.11. Ранговый дисперсионный анализ Краскела-Уоллиса
Тема 5. Краткое введение в дисперсионный анализ
5.1. Что такое дисперсионный анализ?
5.2. Тест на нормальность распределения
5.3. Однофакторный дисперсионный анализ: вычисления «вручную»
5.4. Однофакторный дисперсионный анализ (ANOVA) в пакете Statistica
5.5. ANOVA и критерии Стьюдента и Фишера: что лучше?
5.6. Два однофакторных дисперсионных анализа: вычисление «вручную»
5.7. Двухфакторный дисперсионный анализ: вычисление «вручную»
5.8. Двухфакторный анализ с помощью ANOVA в пакете Statistica
Тема 6. Сравнение распределений
6.1. Примеры проблем, требующих сравнения распределений
6.2. Определение связи качественных признаков с помощью кросстабуляции
6.3. Сравнение распределений с помощью модуля непараметрической статистики
Тема 7. Связь между признаками
Тема 8. Кластерный анализ
8.1. Сущность кластерного анализа
8.2. Пример выполнения кластерного анализа "на пальцах"
8.3. Принципиальные ограничения и недостатки кластерного анализа
Тема 9. Метод главных компонент
9.1. Сущность метода (на простейшем примере)
9.2. Переход к начальным данным с большим количеством измерений
Тема 10. Дискриминантный анализ
10.1. Предназначение и основная логика дискриминантного анализа
10.2. Пример выполнения дисперсионного анализа: морфометрические признаки лягушек
10.3. Поиск более эффективных способов разделения групп
Тема 11. Некоторые методы, характерные для зоологии и экологии
11.1. Анализ флуктуирующей асимметрии
11.2. Пример анализа данных о флуктуирующей асимметрии
Программа раздела большого практикума «Статистический анализ данных в зоологии и экологии»
Дополнительные материалы:
М. А. Гхазалі. Статистичні методи в зоології. Матеріали відкритих лекцій, прочитаних в інституті зоології імені І.І.Шмальгаузена у 2017/2018 навчальному році для аспірантів 1-го курсу
Лекція 1. Статистичне дослідження
Лекція 2. Статистичні оцінки
Лекція 3. Елементарні тести
Лекція 4. Лінійні моделі
Лекція 5. Багатовимірна статистика (частина)
Д. Шабанов (2006). Ложь, наглая ложь и…
Д. Шабанов (2009). Кластеры, клады и химера объективности
К. П. Воробьев (2008). «Формат современной журнальной публикации по результатам клинического исследования. Часть 4. Биостатистика»
Перспективные темы для расширения курса:
Использование СУБД Microsoft Access для создания зоологических баз данных.
Тема 1. Основные понятия биостатистики
1.1. Что такое биостатистика и зачем она нужна
Статистический анализ результатов биологических исследований позволяет решать несколько типов задач:
1. наглядно представлять результаты описания разнообразия изучаемых объектов;
2. обоснованно (с определенной вероятностью ошибки) принимать или не принимать предположения о наличии закономерностей, отражающихся в варьировании изучаемой величины;
3. обнаруживать неявные закономерности, скрытые в варьировании изучаемых данных.
Не следует думать, что существует какая-то особая биологическая статистика, принципиально отличающаяся от математической статистики вообще. Однако изменчивость биологических объектов обладает определенными особенностями, отличающими их, к примеру, от изменчивости финансовых показателей или результатов технологических процессов на производстве. Это приводит к тому, что набор методов, используемых в биологии, отличается от такового в других областях применения статистики. Кроме того, следует помнить, что статистическое исследование в биологии не является самоцелью: оно подчинено задачам биологического исследования и не может быть полностью интерпретировано вне изучаемой биологической проблемы. Однако не только анализ данных должен быть подчинен логике биологического исследования; оно и само должно строится с учетом будущего анализа. Сбор эмпирических данных и постановка экспериментов должны заранее учитывать, как именно будет организован анализ получнных данных. Итак, хотя применение статистики в биологии невозможно полностью отграничить от математической статистики как таковой или изучаемых с помощью тех или иных методов разделов биологии, оно все равно составляет особую отрасль науки, особый комплекс проблем и способов их решения. Для этой отрасли можно использовать термин, предложенный в 1899 году Френсисом Гальтоном — биометрия. Поскольку термин «биометрия» перехватили специалисты по идентификации личности на основании индивидуальных признаков, во многих случаях проще оказывается использовать термин биостатистика.
Объекты, которые изучает биология, обладают высоким уровнем уникальности. Практически в любом биологическом феномене проявляются как общие закономерности, так и влияние особых обстоятельств, часто связанных с той или иной уникальностью биосистем. Это означает, что для биологических исследований очень важны методы, позволяющие увидеть общие закономерности, проявляющиеся за изменчивостью частных проявлений. Возможно, поэтому биологи внесли большой вклад в развитие статистики в целом. Результаты работ Френсиса Гальтона, Карла Пирсона, Рональда Фишера составляют важную часть не только биостатистики, но и математической статистики в целом.
1.2. Вероятность
Статистически можно изучать повторяемые события. Например, мы вслепую выбираем кроликов из ящика. Кролики могут быть черными или белыми. Каждый выбор — элементарное событие. Человек засовывает руку в отверстие ящика и хватает там какого-то кролика… Можно ли узнать, какого кролика он схватил? Нет (если нет иных источников получения информации и иных факторов, влияющих на результат). Можем ли мы узнать, каково соотношение черных и белых кроликов в ящике? Тоже нет.
Как только кролик будет извлечен наружу, мы не просто узнаем, какого он цвета. Мы сможем кое-что узнать о составе кроликов в ящике. Например, если вытащен белый кролик, мы можем утверждать, что в ящике был как минимум один белый кролик. Немного... Однако если последовательно вытащить 10 кроликов, по составу группы кроликов, собирающихся у ног вытаскивающего их человека, можно высказать более детальное предположение о составе кроликов в ящике. Эти предсказания основываются на феномене вероятности, проявляющейся в регулярных, повторяющихся событиях. Вероятность – числовая мера возможности события. Вероятность 1 означает, что событие произойдет наверняка, а вероятность 0 – что оно невозможно.
Предположим, в ящике 50 белых и 50 черных кроликов. Какова вероятность случайно выбрать белого кролика при однократном выборе? Из общего количества возможных исходов (100) этому условию соответствует 50, значит вероятность — 50/100 = 1/2 = 0,5.
А надо ли рассматривать вариант, что, например, в вынутой из ящика руке не было ни одного кролика или, к примеру, два? В реальной жизни — надо, а в ее упрощенной модели, к которой можно применить аппарат основ теории вероятности — можно и не учитывать. Те случаи, когда человек не достал ни одного кролика или достал за раз сразу двух, не соответствуют условиям однократного выбора. Впрочем, если бы читатель этого текста засунул руку в настоящий ящик, заполненный уворачивающимися и лягающимися кроликами, вероятностью, что он ничего не вытащит, пренебрегать было бы нельзя.
А какова вероятность выбрать два кролика одного цвета? Может показаться, что 0,5, хотя на самом деле меньше. После того, как выбран кролик определенного цвета, вероятность выбора второго такого же составляет 49/99 против 50/99. Итак, вероятность выбора двух кроликов одного цвета составляет 49/99 = 0,4949…, а двух белых — 0,24747…
1.3. Генеральная совокупность и выборка
Генеральная совокупность — действительная или гипотетическая совокупность всех объектов, относящихся к изучаемой категории. В большинстве случаев изучать генеральную совокупность невозможно, и исследователи работают с выборками (эмпирическими совокупностями, выборочными совокупностями) — группами объектов, полученных из генеральной совокупности.
Объем генеральной совокупности определяется задачей исследования (и может в существенной степени изменяться при ее переформулировании). Сравнение роста юношей и девушек в группе, изучающей биометрию, может быть исследованием именно этой группы (при этом в выборку попадет вся генеральная совокупность), исследованием студентов конкретного университета (генеральная совокупность при этом хотя бы конечна), студентов вообще или людей вообще (в двух последних случаях генеральная совокупность, по крайней мере, гипотетическая, оказывается потенциально бесконечной).
Существенный парадокс статистики заключается в том, что исследователь работает с выборками, а изучает при этом те совокупности, откуда эти выборки получены.
Можно ли по выборке судить о генеральной совокупности, которая существенно шире этой выборки? В определенной степени, да. Впрочем, понятно, что не всякая выборка отражает состав генеральной совокупности, из которой она получена. Можно ли брать выборку, по которой судить о изменчивости роста людей, из числа студентов? Нет, поскольку в эту выборку попадут люди преимущественно молодого возраста, которые захотели получать высшее образование и смогли поступить в соответствующий вуз. Такая выборка является смещенной. Чтобы получить полностью случайную выборку, следовало бы организовать процесс ее формирования таким образом, что любой из объектов в составе генеральной совокупности имел бы одинаковую вероятность попадания в выборку. В большинстве случаев такой отбор практически неосуществим. Тем не менее, для изучения генеральной совокупности следует использовать только репрезентативные (представительные) выборки, при формировании которых отклонения от случайного характера при их формировании не могут привести к существенному смещению выборки.
Неслучайность формирования выборок, с которыми работает биолог, являются одной из постоянных (и полностью неустранимых) проблем при биологическом исследовании. Представьте себе, что нам надо не доставать черных и белых кроликов из ящика, а определить их соотношение в том или ином местообитании. Как это сделать? Например, выйти в поле и посчитать попадающихся на пути исследователя кроликов того и другого цвета. Однако на черной пахоте более заметными окажутся белые кролики, а после выпадения снега — черные. Может, стоит не полагаться на зрение исследователя, и ловить кроликов ловушками? Однако если белые кролики являются альбиносами, они могут иметь худшее зрение, чем черные, и чаще попадаться в ловушки. Выборка кроликов, которые наблюдались во время маршрутного учета и выборка кроликов, которые попались в ловушки, не являются вполне репрезентативными для оценки генеральной совокупности кроликов, населяющих изучаемую территорию.
Теперь представьте себе, что зоолог пытается оценить состав популяции прытких ящериц. Он посетил местообитание этой популяции в пасмурный ветреный день, перед которым несколько дней подряд шли дожди. В такую погоду вышли на поверхность для поисков корма только молодые особи и беременные (вынашивающие созревающие яйца) самки (те особи, которые испытывают особо сильный голод). Исследователь собрал несколько особей, которые показались ему «типичными», а также еще несколько экземпляров, которые заинтересовали его своей необычностью. В ходе дальнейшего анализа он будет судить о свойствах изучаемой генеральной совокупности (ящериц данной популяции) на основании свойств имеющейся у него выборки. Увы, никакими методами статистического анализа полностью исправить смещение такой выборки будет невозможно.
Рассмотрим шуточный пример. Всем известен фокус, при котором фокусник достает из шляпы кролика (рис. 1.4.1). Откуда берется извлеченный фокусником кролик? Неизвестно… Можно представить себе, что шляпа — «вход» в какой-то аналог ящика с кроликами, наподобие того, на примере которого мы обсуждали понятие вероятности. Процедуру извлечения кроликов из шляпы можно сравнить с получением выборки из генеральной совокупности. Выборкой является извлеченные кролики (возможно — один, возможно — большее количество, один за другим), а генеральной совокупностью — кролики в том «магическом пространстве», из которого они извлекаются.

Рис. 1.4.1. Что мы можем утверждать о том «магическом пространстве», из которого фокусник извлек кролика (т.е. что мы в данном случае можем узнать о генеральной совокупности по полученной нами выборке)?
Там был по крайней мере один белый кролик…
Предположим, фокусник вытаскивает кроликов вслепую: что ухватит рука, засунутая в шляпу, то он и вытащит. Просунув руку в одну шляпу, он вытащил белого кролика, а просунув в другую — черного (рис. 1.4.2).
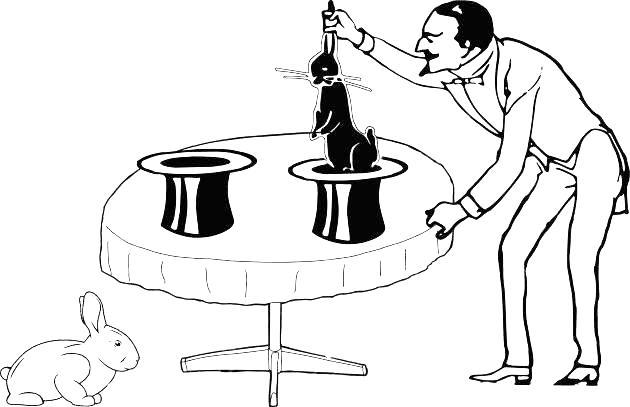
Рис. 1.4.2. Из другой шляпы появился другой кролик, черный… В том пространстве, куда ведет правая шляпа, был, по крайней мере, один черный кролик. А две шляпы ведут в одно пространство, или в разные (иначе говоря, две выборки получены из одной генеральной совокупности или из разных)?
У нас недостаточно оснований для выбора одного из этих вариантов. Может, две выборки получены из одной генеральной совокупности, где есть и черные, и белые кролики, а возможно — из разных совокупностей
Можем ли мы по составу кроликов из двух выборок, соответствующих двум шляпам, установить, получены ли они из одной генеральной совокупности? Иногда полученные нами данные бесполезны для выбора какой-либо из взаимоисключающих возможностей, а иногда они могут быть основанием для обоснованных предположений (рис. 1.4.3).
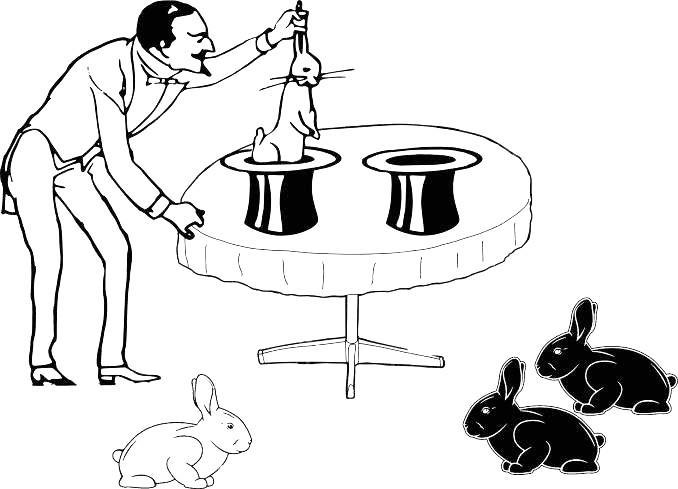
Рис. 1.4.3. Информации для принятия решения стало больше…
Если мы примем, что через две шляпы фокусник дотягивается до двух разных совокупностей кроликов, нам не понадобится никаких дополнительных предположений. Если обе выборки получены из одной генеральной совокупности, нам придется предположить, что реализовался не самый вероятный вариант
Какова вероятность того, что фокусник получит в одной выборке два белых кролика, а с другой — два черных, если он берет их из одной генеральной совокупности? Какое мы можем ожидать соотношение белых и черных кроликов в генеральной совокупности (если она одна)? Мы точно знаем, что там есть и белые, и черные, а их соотношение мы можем оценить по объединенной выборке (мы, в таком случае, предполагаем, что отличия между кроликами из разных шляп — следствие одной лишь случайности). Самый вероятный вариант — белых и черных поровну, так как именно это соответствует общей полученной выборке.
Засунув руку в первый раз в одну из шляп, фокусник вытащил какого-то кролика. Показанный на рис. 1.4.3 вариант реализуется в том случае, если из этой шляпы будет вытащен кролик того же цвета (т.е. произойдет событие, вероятность которого мы оценили как ½), а из другой шляпы два раза подряд будут вытащены кролики иного цвета (т.е. произойдет два независимых события, вероятность каждого из которых — тоже по ½). Таким образом, такое распределение, как на рисунке, получится в случае общего пространства лишь в одном случае на восемь попыток. Вероятнее предположить, что совокупности кроликов разные, хотя, конечно, для того, чтобы отбросить предположение о том, что кролики берутся из одной общей совокупности, оснований у нас недостаточно…
Впрочем, возможны случаи и посложнее (рис. 1.4.4)…
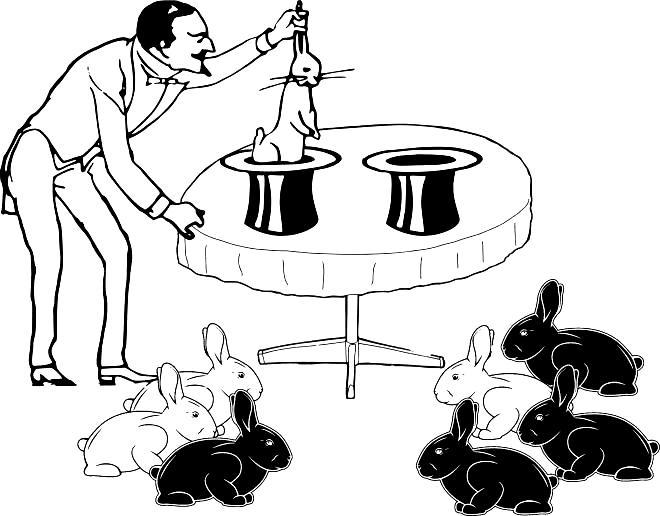
Рис. 1.4.4. Информации еще больше, но расчет вероятности не столь тривиален, как в предыдущем случае
Общее соотношение белых и черных кроликов по-прежнему одинаково. Вероятность того, что в одной выборке соотношение окажется 1 к 3, а в другой — 3 к 1 (без учета того, в каком порядке извлекались кролики в каждой выборке) оказывается той же, что и в предыдущем примере: при заданных численностях выборок показанный на рисунке исход наблюдается в одном случае из восьми.
А как изменятся наши оценки, если выборки станут больше, а отличия между ними — нагляднее (рис. 1.4.5)?
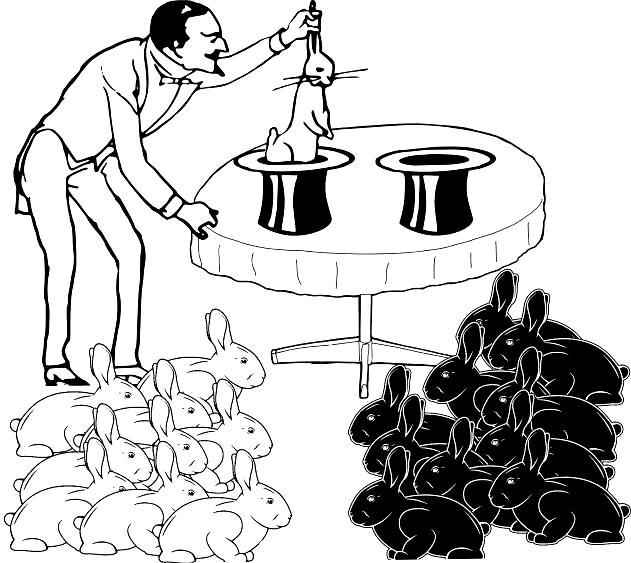
Рис. 1.4.5. В этом случае на вопрос, в одно «магическое пространство» запускает фокусник руки через разные шляпы, или в разные, можно дать весьма вероятный ответ: в разные. Если бы пространство было одно, разделение на 10 кроликов одного цвета в одной выборке и 10 кроликов другого цвета — в другой, могло бы наблюдаться лишь в одном случае на 524288 попыток
Если выборки кроликов, полученные через две шляпы, сильно отличаются (из одной шляпы — 10 белых, из другой — 10 черных), почти наверняка фокусник вытаскивает кроликов из разных совокупностей. Вероятность такого исхода — единица, деленая на 219. Отбросив предположение о столь невероятном событии, мы почти наверняка не ошибемся. Итак, можно принять: в случае, показанном на рис. 1.4.5 шляпы ведут в разные пространства. Однако важно помнить: мы не доказали различие пространств, в которые ведут шляпы, а лишь получили основания с высокой вероятностью предполагать их отличие.
Можно было бы предположить, что в том случае, если выборки не отличаются по составу (рис. 1.4.6), мы могли бы принять противоположное решение, и предположить, что обе шляпы являются порталами для попадания в одно и то же место. Однако такое решение было бы неправильным. Мы установили только то, что предположение об одинаковом соотношении белых и черных кроликов в совокупностях, к которым ведут правая и левая шляпы на рис. 1.4.6, вполне вероятное с точки зрения сравнения извлеченных из них кроликов. Но у нас нет никаких оснований выбрать между предположениями о том, что это два разных пространства с одинаковым составом, или же что это одно общее пространство.

Рис. 1.4.6. Согласуется ли наблюдаемая в этом случае картина с тем предположением, что через правую и левую шляпы фокусник засовывает руки в разные «магические пространства»? Вполне согласуется!
Итак, случай на рис. 1.4.5 дает основания для определенного вывода, а случай на рис. 1.4.6 — нет! Это — отражение общей закономерности: сравнивая две выборки мы иногда можем доказать, что они происходят из разных генеральных совокупностей (т.е. обосновать, что противоположное заключение является крайне маловероятным), но не можем доказать, что они происходят из одной совокупности! Впрочем, можно обосновать, что отличие между совокупностями, из которых взяты две выборки, с той или иной вероятностью не превышает определенного уровня…
В случае сравнения выборок, которое мы рассматривали в этом примере, вероятность того, что выборки получены из одной совокупности и отличия между ними являются следствием случайности, называется статистической значимостью предположения о том, что генеральные совокупности, из которых получены выборки — разные. В иных случаях (например, при изучении связи между изменчивостью двух признаков) статистическая значимость определяется аналогичным образом — это вероятность того, что зарегистрированный эффект является следствием случайности. Коротко можно сформулировать следующее: уровень значимости — это вероятность того, что зарегистрирован просто результат случайности при формировании выборки.
Что означает фраза "результат статистически значим"? Она означает, что случайное возникновение этого результата очень маловероятно, что у нас есть все основания считать результат неслучайным, отражающим особенности того, что мы изучаем.
Чтобы формализовывать подобные логические выборы, принято формулировать две гипотезы, выбор между которыми нужно сделать в ходе статистического исследования.
Нулевая гипотеза (H0) утверждает, что между совокупностями, из которых взяты выборки, нет отличий (а разница между выборками — следствие случайности в ходе их формирования).
Альтернативная гипотеза (H1) утверждает, что отличия между выборками отражают отличия между совокупностями, откуда они получены.
Однозначно выбрать одну из этих возможностей нельзя, и всегда сохраняется возможность ошибки. Нужно по имеющимся данным о составе выборок оценить вероятность справедливости нулевой и альтернативной гипотез и выбрать оптимальное решение. Для этого выбора используются статистические критерии — правила, позволяющие делать такой выбор.
Нулевая и альтернативная гипотеза могут быть ненаправленными (важен сам факт отличия между совокупностями, откуда взяты выборки), а могут быть и направленными (например, важно, что определенное воздействие повышает значение признака; в совокупности подвергнутых воздействию объектов значение признака выше). К примеру, когда мы определяем, влияет ли пол на длину хвоста, мы можем рассматривать как примеры такого влияния и тот случай, когда хвост у самок длиннее, чем у самцов, и тот, при котором он короче. Когда мы определяем, «работает» ли новое лекарство, случаи, когда оно способствует выздоровлению и когда оно препятствует выздоровлению, представляются совершенно различными. Альтернативная гипотеза должна заключаться именно в том, что лекарство способствует выздоровлению. Итак, в первом случае следует применять ненаправленные критерии, а во втором — направленные.
Уровень статистической значимости — это вероятность того, что мы сочли различие существенным (приняли альтернативную гипотезу), а они на самом деле случайны. Можно определить уровень статистической значимости как вероятность того, что приняв альтернативную гипотезу в ситуации, когда на самом деле верна нулевая гипотеза, мы совершили ошибку I рода. Ошибкой II рода называется принятие нулевой гипотезы, когда верна альтернативная. Обычно ошибки I рода оказываются более опасными. Вероятность ошибки первого рода обозначается как α; а второго рода — как β. В соответствии с этим мощность критерия можно определить как = 1 — β.
Часто приходится наблюдать примеры неправильного употребления слов "достоверность" и "значимость". Понятие "статистическая значимость" (или просто "значимость") имеет четкую математическую трактовку. Статистическая значимость (significance) определенного результата (например, регистрации разницы между группами данных или связи между двумя переменными) — низкая вероятность его случайного возникновения. Утверждение "две выборки отличаются статистически значимо" означает, что вероятность их получения из одной совокупности настолько низка, что можно считать доказанным их получение из разных совокупностей. "Достоверность" — намного более широкое понятие, которое может использоваться в самых разных сферах (от юриспруденции до философии) и не имеет математического определения. Его используют для обозначения обоснованного, доказательного знания. Утверждение "выводы диссертации достоверны" означает, что они обоснованы логикой построения и изложения материала. Запомните: достоверные выводы делаются на основании статистически значимых результатов!
Кстати, при неправильной организации эксперимента или при ошибках интерпретации недостоверные выводы могут ссылаться на множество статистически значимых феноменов...
В подавляющем большинстве источников принято говорить просто об "уровне значимости". Это ни в коем случае не является ошибкой, и такое словоупотребление вполне допустимо. Однако на том основании, что данный текст носит учебный характер, его автор будет стараться во всех случаях использовать полную формулировку: понятие "статистическая значимость"; так проще напоминать о его статистической природе.
1.6. Признаки
При описании каких-то объектов исследователи фиксируют значение тех или иных признаков – характеристик, по которым сравниваемые объекты могут отличаться друг от друга. Признаки могут иметь различную природу.
Таблица 1.6.1. Категории признаков
|
Категории признаков |
Выражается |
Пример |
|
|
Количественные |
Метрические |
Число из непрерывного ряда |
Длина тела лягушки |
|
Меристические |
Целое число |
Количество полос на голени |
|
|
Ранговые |
Целое число (ранг), причем разница между рангами не является мерой отличия между самими объектами |
Ранг длины пальцев передней конечности (1 – самый длинный, 2 – следующий по длине и т.д.) |
|
|
Качественные (атрибутивные) |
Множественные |
Определенное качество из некоего набора |
Цвет спины |
|
Альтернативные |
Одно состояние из двух возможных (есть – нет) |
Наличие дорзомедиальной полосы |
|
Признаки из разных групп отличаются по своим свойствам. Например, особь, у которой 4 полосы на голени на столько же полос отличается от особи, у которой их 3, насколько эта особь отличается от той, у которой их 2. В то же время относительно особей, которые отличаются по рангу длины первого пальца на передних конечностях, невозможно сказать, на какую величину палец у особи со рангом 4 короче, чем у особи с рангом 3, а разницу между особями с рангом 4 и 3 невозможно сравнить с разницей между особями с рангами 3 и 2.
Итак, признаки – это характеристики, по которым объекты можно сравнивать друг с другом. Результат описания особи по какому-то признаку называется значением этого признака или просто значением. При работе с компьютерной программой то, что записывается в отдельную ячейку таблицы данных, проще всего называть термином «значение» (хотя существуют и иные варианты, например, «дата»).
1.7. Распределения, статистики и параметры
Распределение — функция, описывающая вероятность тех или иных значений случайно варьирующей величины. То, что монета может с равной вероятностью упасть орлом или решкой, задает распределение исходов падения монет.
Случайные величины (и их распределения) могут быть дискретными и непрерывными. Количественные и счетные признаки имеют дискретные распределения, метрические — непрерывные.
Выборки можно описывать, предполагая, что распределение величин в них подчинено какому-то закону, характерному для генеральной совокупности, из которой она получена.
Предположим, изученная выборка охарактеризована результатами каких-то измерений. Для выборки можно вычислить ее среднее значение. Если выборка полностью описана, ее среднее можно определить вполне точно. На основании выборочного среднего можно с определенной точностью судить о среднем значении генеральной совокупности, откуда эта выборка получена.
Математические величины, характеризующие выборку, называются статистиками и обозначаются латинскими буквами; характеризующие генеральную совокупность — называются параметрами и обозначаются греческими буквами.
В типичном случае в ходе биометрического исследования по статистикам выборки судят о математических величинах, характеризующих генеральную совокупность — ее параметрах.
Таблица 1.7.1. Наиболее распространенные статистики и соответствующие им параметры генеральной совокупности
|
Статистики |
Параметры |
|
Численность выборки — n. |
|
|
Среднее арифметическое — |
Генеральное среднее — |
|
Стандартное отклонение — s; |
Генеральное стандартное отклонение — |
Среднее арифметическое (Mean) 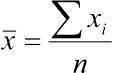 , где
, где  — среднее арифметическое изучаемой величины x ; n — число элементов в выборке; xi — отдельные значения величины x, от x1 до xn. Отдельные
— среднее арифметическое изучаемой величины x ; n — число элементов в выборке; xi — отдельные значения величины x, от x1 до xn. Отдельные  , полученные для разных выборок, можно рассматривать как выборочные оценки генеральной средней
, полученные для разных выборок, можно рассматривать как выборочные оценки генеральной средней 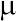 (среднего арифметического генеральной совокупности, включающей всю совокупность объектов, представленных изучаемой выборкой).
(среднего арифметического генеральной совокупности, включающей всю совокупность объектов, представленных изучаемой выборкой).
Варианса, среднеквадратичное отклонение (Variance). Среднеквадратичное отклонение генеральной совокупности могло бы быть вычислено как 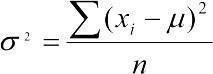 , но для такой оценки нужно было бы перебрать все элементы генеральной совокупности. В действительности этот параметр всегда определяется для определенной выборки, в которую, скорее всего, не попадут самые редкие и самые отклоняющиеся от среднего значения. Значит, выборочное среднеквадратичное отклонение, которое обозначается как s2, надо высчитывать с поправкой. Для этого используется формула
, но для такой оценки нужно было бы перебрать все элементы генеральной совокупности. В действительности этот параметр всегда определяется для определенной выборки, в которую, скорее всего, не попадут самые редкие и самые отклоняющиеся от среднего значения. Значит, выборочное среднеквадратичное отклонение, которое обозначается как s2, надо высчитывать с поправкой. Для этого используется формула 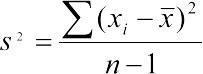 . Величина df=n-1 получила название числа степеней свободы. Можно считать, что при известном
. Величина df=n-1 получила название числа степеней свободы. Можно считать, что при известном  изменять можно значения все элементов выборки, кроме последнего (т.е. их количества, равного n-1): когда определены все остальные значения и среднее, последнее из значений выборки однозначно определяется этими величинами.
изменять можно значения все элементов выборки, кроме последнего (т.е. их количества, равного n-1): когда определены все остальные значения и среднее, последнее из значений выборки однозначно определяется этими величинами.
По-русски вариансу часто называют дисперсией (от лат. dispersio — рассеяние; отсюда и происходит название дисперсионного анализа). Иногда указывают, что термин дисперсия стоит применять только для обозначения самого факта рассеяния отдельных значений вокруг среднего, а описанную меру называть, по аналогии с английским языком, вариансой. Варианса является квадратом стандартного отклонения (Standard Deviation), которое обозначается s и вычисляется, естественно, 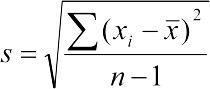 .
.
Иногда используются и иные статистики, характеризующие выборки. К их числу можно отнести размах (разницу между минимальным и максимальным значением), медиану (значение, которое находится ровно в середине упорядоченного ряда элементов выборки, так, что половина элементов выборки оказывается меньше этого значения, а половина – больше), моду (самый многочисленный класс значений в выборке), среднее линейное отклонение, среднее геометрическое и т.д. Хороший анализ этих и иных статистик находится здесь.
В соответствии с законом больших чисел, восходящем к Я. Бернулли (1713) и доказанному П.Л. Чебышевым в XIX в., по мере увеличения выборки выборочные статистики стремятся к параметрам генеральной совокупности. Чем меньше выборка, тем вероятнее отклонение выборочных статистик от параметров генеральной совокупности.
Если на метрический признак оказывает влияние множество случайных воздействий, он приобретает нормальное распределение. Графически это распределение описывается нормальной кривой, которая однозначно задается всего двумя параметрами: 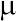 и
и 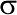 .
.
В нормальном распределении совпадают среднее, медиана и мода. 99,7% наблюдаемых значений при нормальном распределении находится в пределах 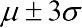 (правило трех сигм).
(правило трех сигм).
Эмпирические распределения могут напоминать нормальные, тем не менее отличаясь от них. Самые распространенные отличия — асимметрия и эксцесс.
1.8. Параметрические и непараметрические статистические методы и критерии
Статистические критерии (правила, позволяющие сделать выбор между нулевой и альтернативной гипотезой) можно разделить на параметрические (те, в процедуре которых предусматривается, что сравниваемые выборки получены из генеральных совокупностей с определенным, чаще всего нормальным, распределением) и непараметрические, свободные от параметров (не требующие никаких предположений о характере распределения исследуемых совокупностей). Итак, если мы не знаем, как распределены сравниваемые нами величины, "по умолчанию" можно использовать непараметрические методы. Однако большинство непараметрических методов обладают меньшей мощностью (1 — β, где β — вероятность "упустить" различие, принять нулевую гипотезу в то время, когда верна альтернативная), чем параметрические (и это естественно, ведь параметрические методы уже кое-что "знают" о распределениях сравниваемых величин).