 |
||||
|
← |
Д.А. Шабанов, М.А.Кравченко. Статистический анализ данных в зоологии и экологии |
→ |
||
|
Тема 10. Дискриминантный анализ |
Тема 11. Некоторые методы, характерные для зоологии и экологии |
|||
|
Биостатистика-13 |
Биостатистика-15 |
|||
Тема 10. Дискриминантный анализ
10.1. Предназначение и основная логика дискриминантного анализа
Дискриминантный анализ — это статистический метод, предназначенный для изучения отличий между двумя или большим количеством групп объектов с использованием данных о разнообразии нескольких признаков, отличающих эти объекты друг от друга. Типичная для дискриминантного анализа задача — определение тех признаков, которые лучше всего дискриминируют (отличают) объекты, относящиеся к разным группам. После того, как определены наилучшие способы дискриминации имеющихся групп (т.е. проведена интерпретация отличий между ними), этот способ анализа позволяет проводить классификацию образцов, принадлежность которых к той или иной группе заранее неизвестна. Дискриминантный анализ разработал Рональд Фишер (1890—1962), классик биометрии и эволюционной биологии.
Пояснить, как может быть использован дискриминантный анализ, проще всего на примерах. Предположим, нас интересуют различия между женскими и мужскими скелетами (или между формой тела диплоидных и триплоидных зеленых лягушек). Мы рассматриваем совокупность скелетов мужчин и женщин (или морфологических признаков диплоидов и триплоидов) и определяем, какие признаки лучше всего дискриминируют эти группы. После этого мы можем использовать полученные нами результаты для того, чтобы определить половую принадлежность скелетов, пол которых нам изначально не известен (или определять плоидность лягушек по форме их тела).
Алгоритм дискриминантного анализа рассматривает многомерное пространство признаков, в котором расположены изучаемые объекты (состояние признаков каждого объекта определяет его положение в таком пространстве). В этом пространстве выбирается такая каноническая дискриминантная функция, которая в наибольшей степени отражает различия между группами объектов. Эта процедура напоминает процедуру, используемую при анализе главных компонент, за тем исключением, что при компонентном анализе выбираются главные компоненты, на которые проецируется максимум информации о разнообразии всех объектов, а дискриминантный анализ максимизирует отличия между заранее заданными их группами. После того, как выбрана первая такая функция, на основании оставшейся информации выбирается вторая каноническая дискриминантная функция.
С другой стороны, дискриминантный анализ близок к дисперсионному. Его задачу можно сформулировать так. В ходе дискриминантного анализа выбирается дискриминантная функция (переменная или линейное сочетание переменных) которая позволяет отличать группы друг от друга и значение которой может быть использовано для того, чтобы предсказать, к какой группе принадлежит каждый объект. Ситуацию можно рассмотреть и в терминологии одномерного дисперсионного анализа (ANOVA). Являются ли статистически значимыми отличия групп по характерным для них значениям дискриминантной функции? По какой из дискриминантных функций отличия между группами оказываются наиболее статистически значимыми?
Как выбрать дискриминантную функцию таким образом, чтобы она лучше всего отражала различия между группами? Дискриминантная функция тем лучше, чем плотнее объекты каждой группы расположены вокруг центроидов ("центров тяжести") групп, и чем дальше отстоят центроиды друг от друга. Каждая следующая функция будет вносить все меньший и меньший вклад в дискриминацию рассматриваемых групп. Каждая дискриминантная функция — это некая линейная комбинация дискриминантных переменных, т.е. признаков, характеризующих рассматриваемые объекты. Максимальное количество дискриминантных функций на единицу меньше количества дискриминантных переменных и не превышает количества групп.
Алгоритм дискриминантного анализа основан на двух достаточно важных предположениях. Принимается, что дискриминантные переменные имеют нормальное распределение, и что их дисперсия и ковариация в разных группах является однородной. Небольшие отклонения от математической истинности этих условий являются вполне допустимыми.
"Наиболее важным критерием правильности построенного классификатора является практика". Халафян, 2007
10.2. Пример выполнения дисперсионного анализа: морфометрические признаки лягушек
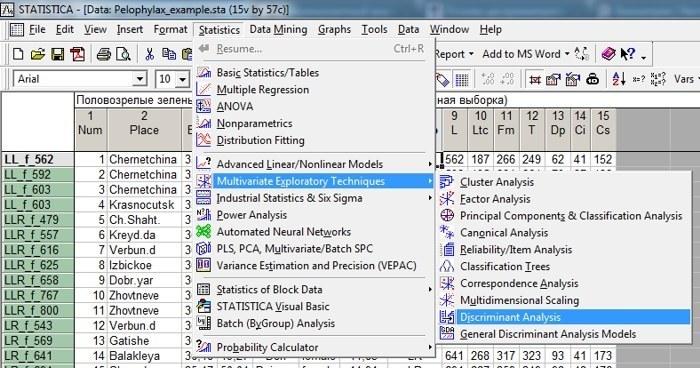
Освоить процедуру дисперсионного анализа проще всего, использовав ее для анализа данных в файле Pelophylax_example.sta. Установим, какие переменные лучше всего осуществляют дискриминацию между лягушками, относящимися к пяти разным генотипам. Для этого воспользуемся модулем Discriminant Analysis в подменю Multivariate Exploratory Techniques из меню Statistics, как это показано на рис. 10.2.1.
Рис. 10.2.1. Вызов модуля дискриминантного анализа
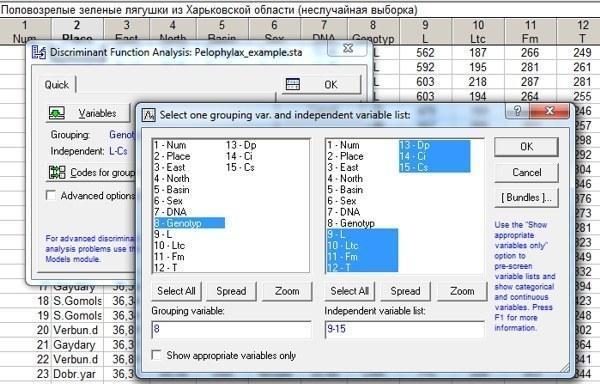
Начнем с того, что рассмотрим все семь морфометрических признаков, включенных в наш анализ. Выберем их в окне Variables так, как это показано на рис. 10.2.2.
Рис. 10.2.2. Выбор группирующей переменной (генотип) и дискриминантных переменных
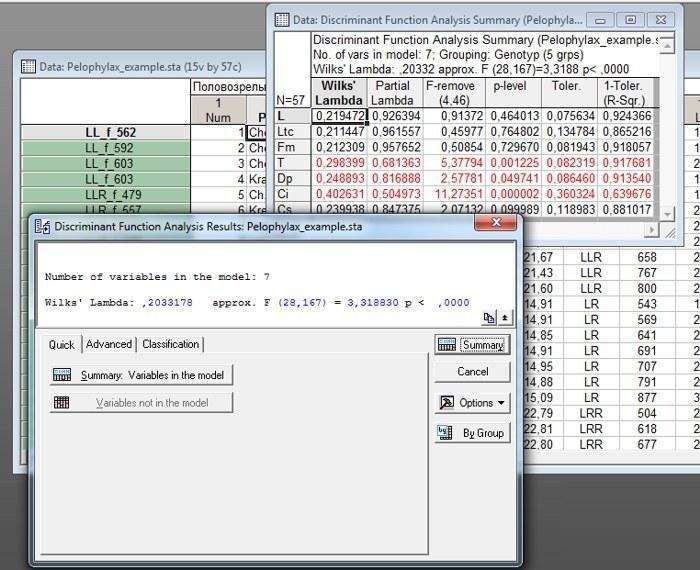
В данном случае выполним анализ с настройками по умолчанию. Его результат показан на рис. 10.2.3.
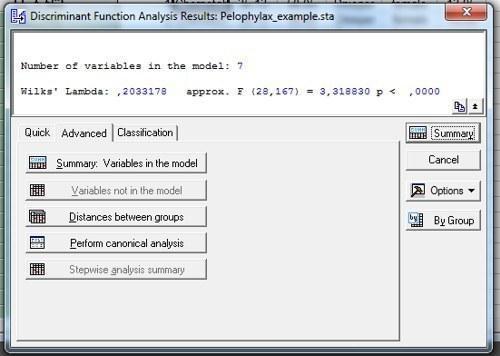
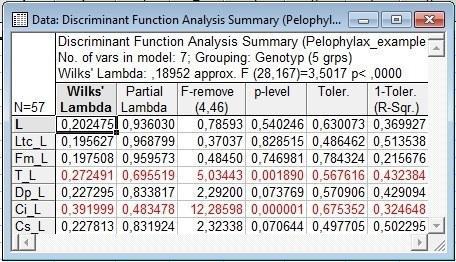
Рис. 10.2.3. После того, как на показанном на предыдущем рисунке диалоге была нажата кнопка OK, появилось окно Discriminant Function Analysis Result. Если в этом окне нажать кнопку Summary, появится таблица с результатами: Discriminant Function Analysis Summary, тоже показанная на этом рисунке
Сейчас следует рассмотреть основные статистики, которые используются для интерпретации результатов дискриминантного анализа. Самые главные из них показаны в верхней части окна Discriminant Function Analysis Result, а более подробные результаты, касающиеся каждой из переменных, отражаются в окне Discriminant Function Analysis Summary (рис. 10.2.3).
Wilk`s Lambda — лямбда Уилкса (статистика Уилкса). Эта статистика вычисляется как отношение детерминанта матрицы внутригрупповых дисперсий (ковариаций) к детерминанту общей ковариационной матрицы. Вникать в детали того, что это означает, мы не будем, и обойдемся простым определением. Лямбда Уилкса — это отношение меры внутригрупповой изменчивости к мере общей изменчивости. Внутригрупповая изменчивость — часть общей, и это означает, что лямбда Уилкса может принимать значения от 0 (группы полностью однородны) до 1 (разделение объектов на группы не приводит к тому, что внутригрупповая изменчивость оказывается меньше общей). Итого, чем меньшее значение имеет лямбда Уилкса, тем лучшим оказывается разделение на группы при дискриминантном анализе.
В верхней части окна Discriminant Function Analysis Result показано общее значение лямбды Уилкса для дискриминантного анализа с учетом всех задействованных переменных. В первом столбце окна Discriminant Function Analysis Summary, напротив каждой из переменных, показано значение лямбды Уилкса для анализа, в котором данная переменная не используется. Если исключение какой-то переменной из анализа привело к существенному ухудшению результата, то мы можем утверждать, что эта переменная вносила в него важный вклад. Итого: чем выше значение лямбды Уилкса в первом столбце окна Discriminant Function Analysis Summary, тем важнее этот признак, а чем ниже общее значение этой статистики, показанной в Discriminant Function Analysis Result, тем качественнее было проведено разделение групп. Постарайтесь не запутаться!
Partial Lambda — частная лямбда. Эта статистика показывает отношение лямбды Уилкса после добавления данной переменной к лямбде Уилкса до добавления переменной. Если переменная вносит хотя бы какой-то вклад в разделение групп, после ее добавления лямбда Уилкса должна уменьшиться. В связи с этим, чем меньшим оказывается значение частной лямбды, тем ценнее данный признак.
F-remove — F-критерий, связанный с исключением данного признака из анализа, а p-level — это уровень его статистической значимости. Если исключение признака приводит к статистически значимому изменению соотношения дисперсий, значит этот признак вносит важный вклад в дискриминацию групп.
Наконец, Toler. — толерантность. Это мера избыточности признака, которая вычисляется, как 1-R2, где R2 — коэффициент множественной корреляции данного признака со всеми остальными признаками, использованными в анализе. Чем ниже толерантность, тем сильнее данный признак связан со всеми остальными. А вот для коэффициента множественной корреляции, который указывается в последнем столбце, ситуация противоположная. Чем выше R2, тем сильнее данный признак связан с остальными, использованными в модели.
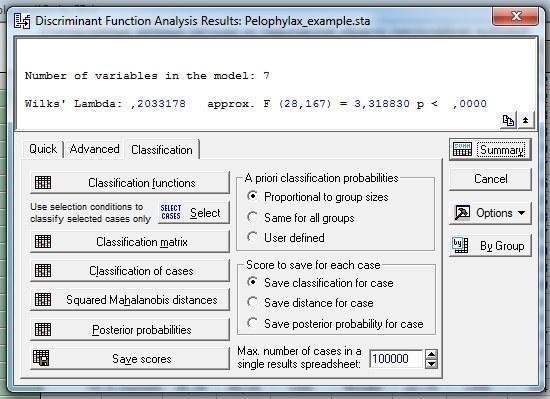
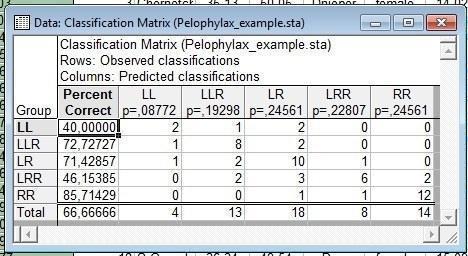
Еще одной важной мерой, позволяющей оценить качество разделения объектов по группам, является процент корректно классифицированных объектов. Чтобы узнать его, надо в коне Discriminant Function Analysis Result перейти на закладку Classification (рис. 10.2.4).
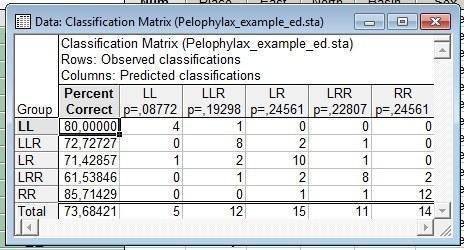
Рис. 10.2.4. Закладка Classification в окне Discriminant Function Analysis Result. Чтобы оценить корректность полученного в результате анализа распределения по группам, надо нажать на кнопку Classification Matrix (см. следующий рисунок)
Рис. 10.2.5. Корректность классификации по использованным в анализе данным. Строки — то, к каким группам в действительности относятся рассматриваемые особи. Столбцы — отражение того, как эти объекты были бы классифицированы (по использованным переменным), если бы то, к каким группам они принадлежат, было бы неизвестным
На рис. 10.2.5 мы можем увидеть, что наш анализ позволил бы правильно определить две трети из рассмотренных особей. Лучше всего определяются особи с генотипом RR (Pelophylax ridibundus), а хуже всего LL — (Pelophylax lessonae).
Однако особенности человеческого восприятия таковы, что никакие статистики (для которых приходится запоминать, увеличение или уменьшение их свидетельствует о возрастании качества разделения) не сравнятся с наглядным графиком, показывающим распределение объектов друг относительно друга. Чтобы получить наглядную картинку, следует выполнить канонический анализ (рис. 10.2.6).
Рис. 10.2.6. В закладке Advanced в окне Discriminant Function Analysis Result можно вызвать канонический анализ (Perform canonical analysis)
Рис. 10.2.7. Окно с результатами канонического анализа. В нем нужно перейти на закладку Canonical scores (канонические корни)...
Рис. 10.2.8. ...и нажать на кнопку Scatterplot of canonical scores
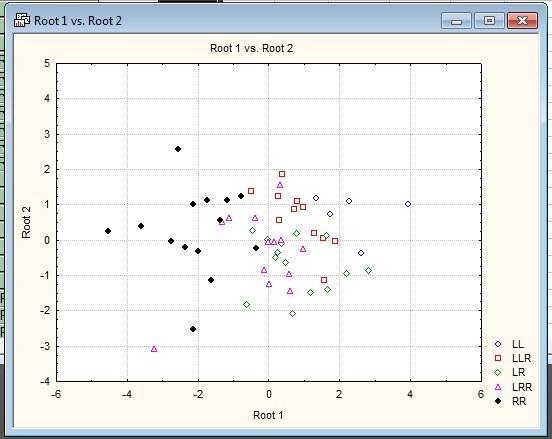
Рис. 10.2.9. Выбрав необходимые канонические корни (обычно — первый и второй), можно увидеть, как располагаются в их пространстве исследованные образцы
Полученную картину уже можно интерпретировать. Мы можем увидеть, что первый канонический корень отражает отличия между Pelophylax ridibundus и Pelophylax lessonae. Гибриды располагаются между родительскими видами, "выстроившись" в порядке отношения родительских геномов. Разделение не абсолютное и включает определенное перекрывание (именно с ним связаны случаи, когда классификация была бы выполнена некорректно).
Напомню, что канонические корни — это те самые канонические дискриминантные функции, которые выбираются так, чтобы они наилучшим образом отражали отличия между группами объектов. Эти корни являются линейными комбинациями дискриминантных переменных (в предельном случае — соответствуют каким-то из переменных). Чтобы посмотреть, как связаны канонические корни и дискриминантные переменные надо нажать на кнопку Factor structure на вкладке Advanced в окне Canonical Analisis. Там показаны коэффициенты корреляции, связывающие каждый канонический корень с каждой дискриминантной переменной.
10.3. Поиск более эффективных способов разделения групп
В предыдущем пункте в дискриминантном анализе использовались "сырые" морфометрические признаки. Можно предположить, что это не самое лучшее решение. Виды и внутривидовые формы животных очень часто отличаются друг от друга пропорциями — соотношениями разных морфометрических признаков. Во многих случаях в зоологических исследованиях удачным оказывается такой вариант: использовать некий признак, который характеризует общий размер, в его абсолютной форме, а все остальные — в виде пропорций, их отношения к признаку, характеризующему размер. В нашем примере, естественно, размер характеризует признак L — длина тела. Шесть остальных признаков можно использовать в виде пропорций — частного от деления их абсолютных размеров на L. Выполним анализ с таким набором признаков. Его результаты показаны на рис. 10.3.1.
Рис. 10.3.1. Результаты дискриминантного анализа, в котором использовалась длина тела и отношения других признаков к длине тела. Обозначениям наподобие T_L соответствуют пропорции, которые вычисляются как T/L
При использовании абсолютных значений признаков лямбда Уилкса была равна 0,20. При переходе к пропорциям она немного уменьшилась, и стала равной 0,19 (0,18952).
Рис. 10.3.2. Корректность классификации при использовании отношений морфометрических признаков к длине тела
Немного улучшилась и корректность классифицирования. Она теперь составляет 73,7% (при использовании "сырых" данных была 66,6%).
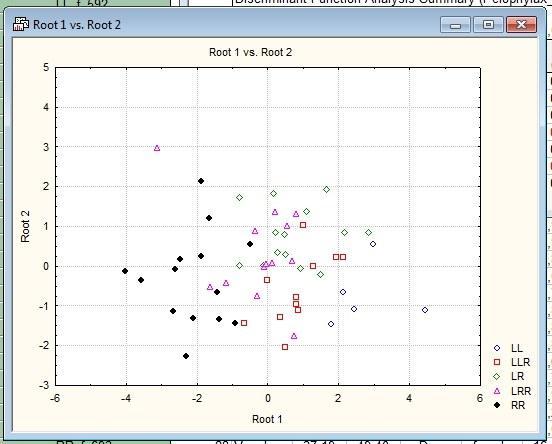
Рис. 10.3.3. Распределение изучаемых объектов в плоскости двух первых канонических дискриминантных функций при использовании данных о длине тела особей и отношениям их промеров к длине тела
Качество разделения особей на плоскости двух канонических корней изменилось несущественно.
Нам не удалось качественно улучшить качество классифицирования, но мы убедились, что используя вместо сырых данных их соотношения, мы можем улучшить результат. А как найти оптимальный набор признаков, который надо использовать для поиска различий между представителями разных генотипов?
Коментарі
Нехватка информации в пункте 10.3
Как задать использование признаков в виде пропорций?
Они должны быть в файле
Перед дискриминантным анализом эти признаки должны быть созданы и рассчитаны. Для этого надо использовать формулы в заголовках столбцов, как это описано в главе об использовании Статистики (наподобие =v1/v2). Конечно, лучше использовать не номера столбцов (потому что при изменении количества столбцов все может "поплыть"), а их имена (английскими литерами без пробелов и знаков; допускается только _)