|
||||
|
← |
Д.А. Шабанов, М.А.Кравченко. Статистический анализ данных в зоологии и экологии |
→ |
||
|
Тема 4 (продолжение). Множественные сравнения |
Тема 4 (продолжение). Непараметрические критерии для сравнения выборок |
|||
|
Биостатистика-05 |
Биостатистика-07 |
|||
4.5. Проблема множественных сравнений
В пункте 4.2. мы сравнили самцов и самок зеленых лягушек из файла Pelophylax_example.sta по длине их тела. Однако в этом файле приведены результаты измерений еще по шести морфометрическим признакам. Сравнить самцов и самок можно не только по всем семи (включая длину тела) морфометрическим признакам одновременно. Вместе с этими измерениями целесообразно рассмотреть также разнообразные индексы — частные от деления одних промеров на другие. Сколько их можно высчитать на основании этих данных, чтобы не рассматривать одну и ту же пару признаков дважды? Шесть промеров можно разделить на длину тела, пять — на первый из этих шести и т.д. Таким образом, можно вычислить 6 + 5 + 4 + 3 + 2 + 1 = 21 индекс.
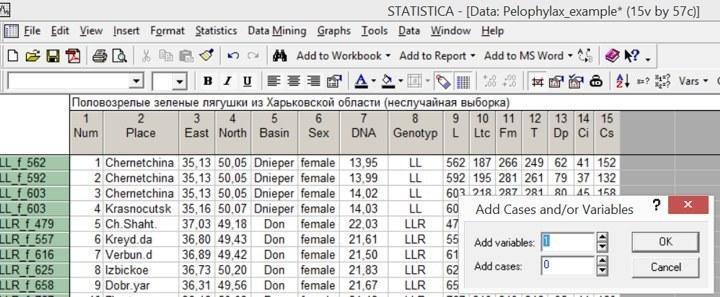
Добавим к файлу Pelophylax_example.sta еще 21 столбец. Самый простой способ это сделать — дважды щелкнуть мышью по серому полю за пределами столбцов (правее переменной Cs на рис. 4.5.1). Естественно, работает и способ Vars / Add.
Рис. 4.5.1. Двойной щелчок по полю справа от столбцов вызвал окно для добавления строк и столбцов. В окошке Add variables надо указать требуемое количество столбцов
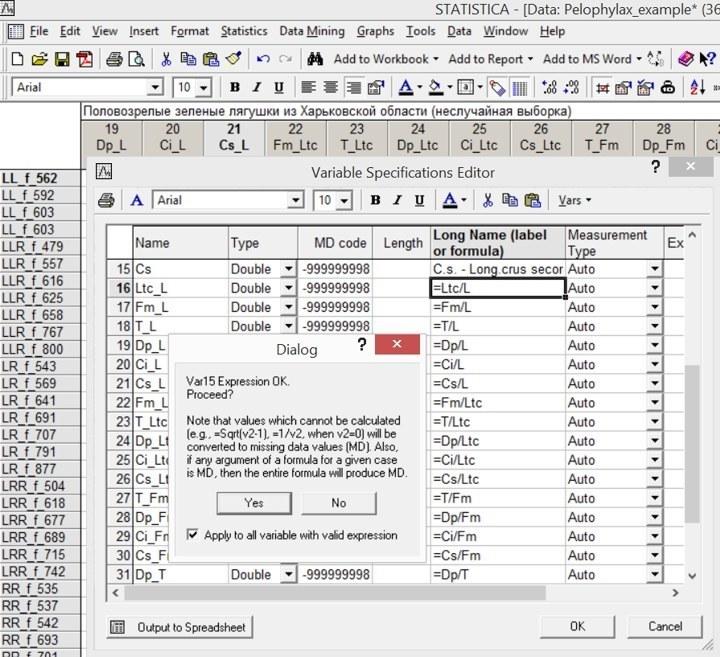
Для добавленных столбцов надо указать названия и задать формулы, по которым они будут высчитываться. Проще всего это сделать в окне All Specs (Vars / All Specs).
Рис. 4.5.2. В окне All Specs добавлены формулы для группы столбцов. После того, как нажата кнопка OK, программа начинает последовательно проверять и пересчитывать формулы, о чем сообщает в специальном окне. Поставив галочку в окошке Apply to all variable with valid expression, можно сделать этот процесс автоматическим
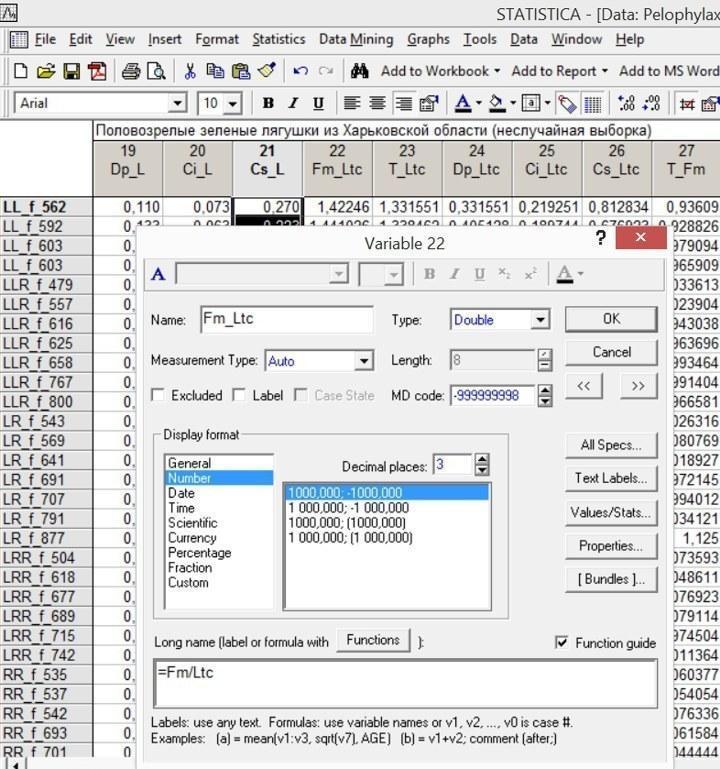
Данные в новых столбцах показываются с избыточной точностью. Можно сделать их отображение более адекватным. Для этого в режиме заголовка столбца (Specs) нужно изменить формат отображения данных (Display format), выбрав режим Number. После этого можно указать необходимое количество десятичных знаков (Decimal places), например, три.
Рис. 4.5.3. Переходить от одного столбца к другому можно с помощью кнопок со стрелками (в верхней правой части окна)
Теперь, как кажется, можно сравнить значения всех метрических признаков и индексов для самцов и самок в нашем файле.
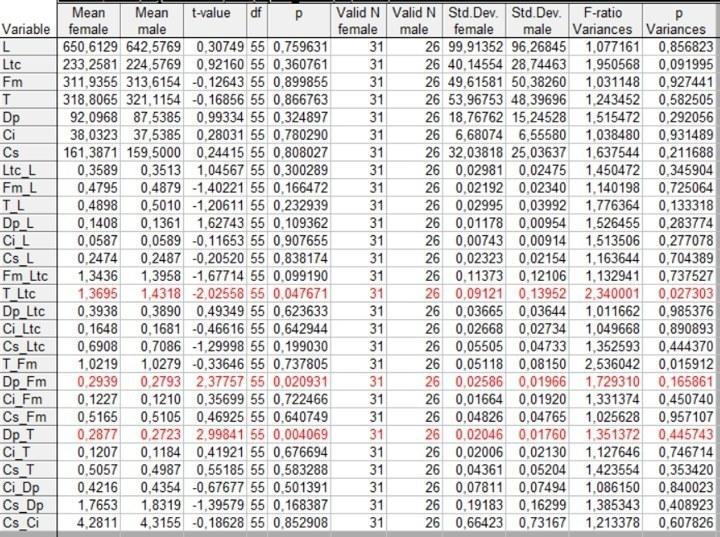
Рис. 4.5.4. Результаты сравнения двадцати восьми признаков по Стьюденту. Признаки, по которым зарегистрированы значения p, меньшие, чем 0,05, выделены красным цветом
Итак, по трем переменным зарегистрированы "значимые" отличия. Самки и самцы "значимо" отличаются по изменчивости индекса T/Ltc (отношение длины голени к ширине головы); по индексу Dp/Fm (отношение длины первого пальца задней ноги к длине бедра) "значимо" отличаются средние значения, характерные для самцов и самок; по индексу Dp/T (отношение длины первого пальца задней ноги к длине голени) два пола отличаются и по среднему значению, и по уровню изменчивости.
Во многих работах, в том числе и таких, которые публикуются в приличных источниках, приводят такие рассуждения, и делают многозначительные выводы из того, что отличия между самцами и самками обнаружились именно по этим признакам. Однако мы должны задуматься на том, что означает полученный результат.
Что означает, что по какому-то признаку уровень статистической значимости для зарегистрированных отличий ниже, чем 0,05? То, что такие отличия, как те, которые были зарегистрированы по этому признаку, могли возникнуть в силу случайности при формировании выборок из одной совокупности не чаще, чем в одном случае из 20. Мы провели сравнение по 28 признакам; по каждому из них мы проводили сравнение по двум критериям. Всего мы провели 56 сравнений. Сколько раз для 56 попыток можно ожидать повторения исходов, которые происходят с вероятностью один случай на двадцать попыток? Два-три раза.
4.6. Эксперимент с получением ложно "значимых" отличий при множественных сравнениях
Давайте подтвердим сказанное в предыдущем пункте специальным экспериментом. Создадим файл, в котором будет проводиться множественное сравнение выборок, заведомо принадлежащих к одной совокупности (случайных данных, сгенерированных в соответствии с одним и тем же распределением). Получим ли мы ложно "значимые" результаты?
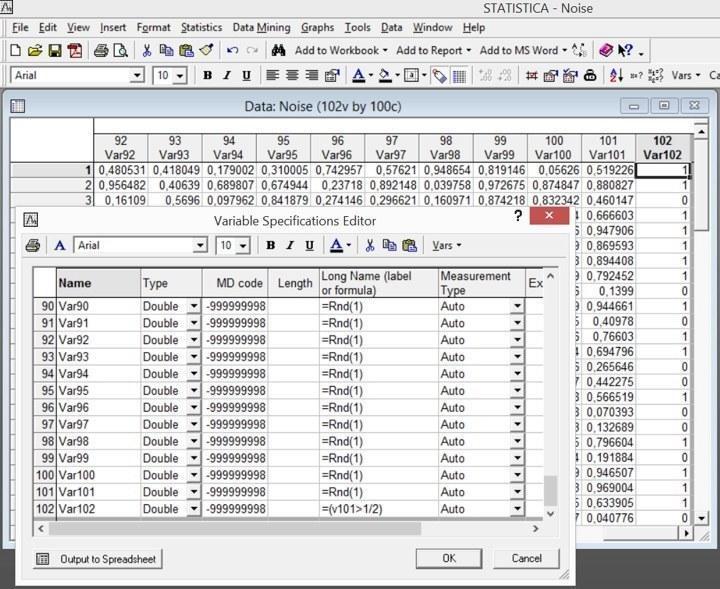
Создадим новый файл статистики: File / New. Укажем для него 102 столбца (Number of variables) и 100 строк (Number of cases). Щелкнем по заголовку первого столбца и в строке для формул укажем: =Rnd(1). Эта формула генерирует в каждой ячейка столбца случайную величину, равномерно распределенную между 0 и 1. В режиме All Specs "растянем" эту формулу на все столбцы, включая столбец № 101. В строку формул столбца № 102 впишем формулу =(v101>1/2). В этом столбце будет стоять 0 (значение в скобках неверное), когда случайная величина в столбце 101 будет меньше 0,5 (т.е. с вероятностью 50%), и 1 — когда эта величина будет больше порогового значения.
Рис. 4.6.1. Экспериментальный файл с данными
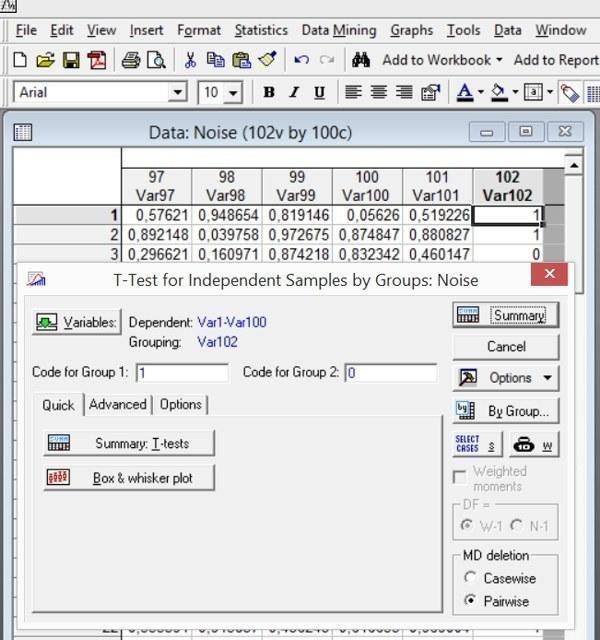
Проведем для этого файла сравнение строк, разбитых на группы в зависимости от значения, которое стоит в 102-м столбце, по 100 признакам (101-й столбец использовать нельзя, так как он связан зависимостью с значением, которое стоит в 102-м столбце).
Рис. 4.6.2. Сравнение по Стьюденту, выполняемое для 100 первых столбцов
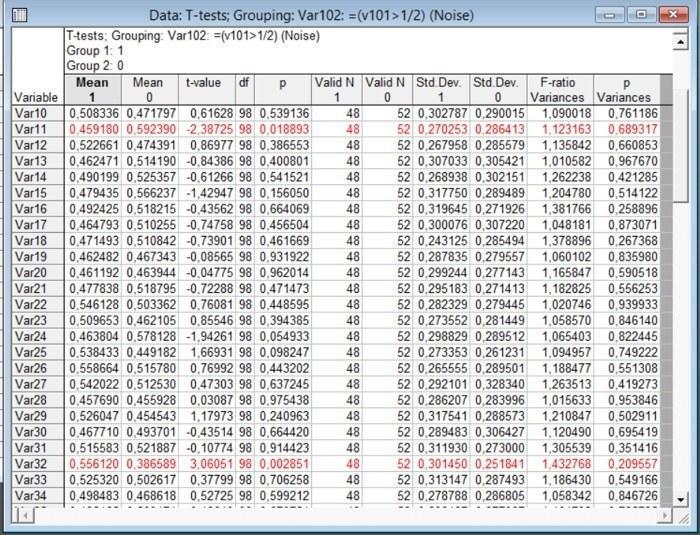
Выполнив сравнение двух групп по 100 признакам, мы увидим достаточно высокое количество "значимых" (т.е. таких, для которых p < 0,05) результатов. Но не забывайте: наш файл заполнен данными, относящимися к одной генеральной совокупности (шумом, который порождается формулой =Rnd(1), случайной равнопемно распределенной величиной). Пересчет данных (с помощью команды Vars / Recalcelate Spreadsheet Formulas..., клавиатурного сокращения Shift+F9 или специальной кнопки с надписью x=?) приведет к тому, что набор "значимых" отличий изменится.
Рис. 4.6.3. Результаты. Обратите внимание на подсвеченные красным "значимые" отличия по некоторым признакам. Это — артефакт метода, следствие использования множественных сравнений без необходимых поправок
Фактически, если в случае множественных сравнений действовать так же, как при единичном сравнении, резко возрастает опасность совершить статистическую ошибку I рода: ошибочно отбросить нулевую гипотезу, в то время, как она верна.
4.7. Поправки на множественные сравнения
Как же следует действовать, чтобы не прийти к ложным умозаключениям? Самое простое решение — использовать поправку Бонферрони, предложенную итальянским математиком Карло Эмилио Бонферрони. Поправку Бонферрони высчитать очень просто. Нужно определить общее количество рассматриваемых статистических гипотез (выборов между нулевой и альтернативной гипотезой), которое можно обозначить как m. Для каждого из этих сравнений следует использовать не уровень статистической значимости α, который был принят для единичных сравнений, а частное от его деления на количество гипотез: α/m. В рассмотренном примере это означает, что в качестве критического уровня статистической значимости надо принять не 0,05, а 0,05/100=0,0005. Как вы понимаете, в этом случае в рассмотренных нами примерах статистически значимых отличий не окажется.
В случае достаточно большого числа множественных сравнений применение поправки Бонферрони имеет существенный недостаток. Занижая критический уровень статистической значимости, мы повышаем вероятность совершить статистическую ошибку II рода — принять нулевую гипотезу в то время, когда верна альтернативная.
Более адекватным (хотя и несколько более сложным в реализации) является метод, который проще всего описать, процитировав блог r-analytics.
«Для преодоления проблем, связанных с низкой мощностью метода Бонферрони, в 1978 г. Стур Холм (Holm 1978) предложил гораздо более мощную его модификацию (часто этот метод называют еще методом Холма-Бонферрони). Этот модифицированный метод основан на алгоритме, который включает следующие шаги:
Исходные Р-значения упорядочиваются по возрастанию: p(1)≤p(2)≤⋯≤p(m). Эти Р-значения соответствуют проверяемым гипотезам H(1),H(2),…H(m).
Если p(1)≥α/m, все нулевые гипотезы H(1),H(2),…H(m) принимаются и процедура останавливается. Иначе следует отвергнуть гипотезу H(1) и продолжить.
Если p(2)≥α/(m−1), нулевые гипотезы H(2),H(3),…H(m) принимаются и процедура останавливается. Иначе гипотеза H(2) отвергается и процедура продолжается.
...
Если p(m)≥α, нулевая гипотеза H(m) принимается и процедура останавливается.
Описанную процедуру называют нисходящей (англ. step-down): она начинается с наименьшего P-значения в упорядоченном ряду и последовательно "спускается" вниз к более высоким значениям. На каждом шаге соответствующее значение p(i) сравнивается со скорректированным уровнем значимости α/(m-i+1)».
(последняя формула в цитируемом источнике написана с ошибкой; здесь эта ошибка исправлена; кроме того, вероятно, более правильным следует считать русское написание фамилии автора "Хольм", а не "Холм" ).
Пример реализации процедуры Хольма-Бонферрони средствами Statistica показан на рис. 4.5.8. В этом примере было проведено 11 сравнений с использованием определенного непараметрического теста. Вычисленные уровни статистической значимости (p) были записаны в столбец US_UB и отсортированы по возрастанию. В столбце i_US_UB проставлены порядковые номера этих сравнений. В столбце a_US_UB вычислены критические значения для каждого из этих сравнений. Наконец, в строку формул столбца Holm_US_UP вписано выражение, принимающее значение 1 если зарегистрированный эффект следует считать статистически значимым, и 0 — если результат признается статистически незначимым. Можно увидеть, что отличия, зарегистрированные в сравнениях под номерами 7, 8 и 9 были бы признаны статистически значимыми, если бы мы каждое из этих сравнений было бы единственным, и те же самые отличия следует считать статистически незначимыми в том случае, если мы проводим одновременно 11 сравнений и используем процедуру Хольма-Бонферрони.
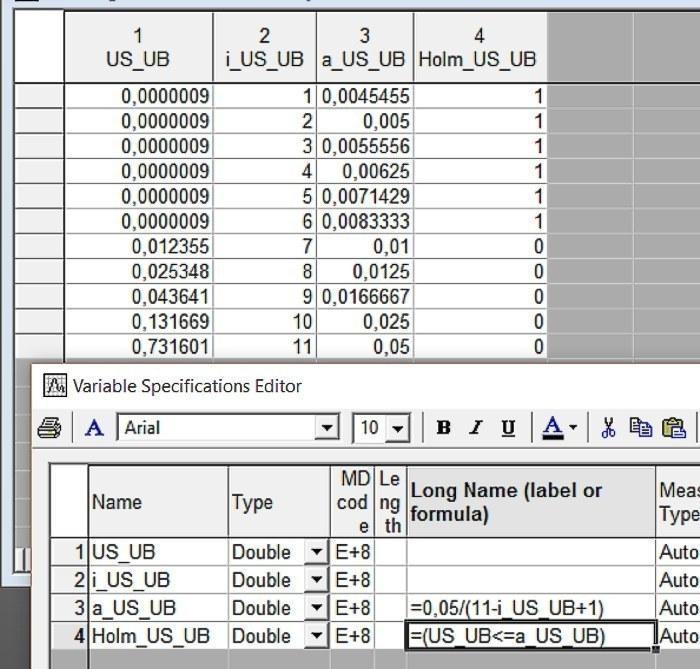
Рис. 4.7.1. Реализация процедуры Хольма-Бонферрони средствами Statistica
Следует особо подчеркнуть, что проблема множественных сравнений касается не только сравнения выборок, но и всех случаев множественного использования статистических критериев. Чтобы убедиться в этом, можете попробовать определить корреляцию между всеми возможными парами признаков из экспериментального файла, сделанного в предыдущем пункте. Результат будет тем же...
Какие бы методы вы не использовали, если вы проводите одновременно несколько статистических тестов, вы должны использовать поправки на множественные сравнения!