Creation of Worlds — 09. Моделі на основі клітинних автоматів

9. Моделі на основі клітинних автоматів

9.1. Гра «Життя» Джона Конвея

Гра «Життя», що була створена Джоном Конвеем, стала варіантом реалізації ідей двох класиків кібернетики: Алана Тьюринга і Джона фон Неймана. Щоб зрозуміти значення цієї гри, потрібно пройти по основних віхах її передісторії.

Машина Тьюринга, запропонована в 1936 році, – це абстрактний виконавець, який реалізує певний алгоритм, переходячи з одного стану в інший. Ідея Тьюрінга полягала в тому, що керуючий пристрій, що здатний знаходитися в кінцевій кількості станів та виконує певні алгоритми, здатен забезпечити всі використовувані людством послідовності дій.

Фон Нейман намагався реалізувати ідею алгоритмічної машини Тьюринга за допомогою клітинного автомата. Клітинним автоматом називається регулярна структура з комірок, кожна з яких може знаходиться в одному з кінцевої кількості станів. Для роботи клітинного автомата потрібно задати його початковий стан і правила переходу комірок з одного стану в інший. До речі, LO Calc та інші електронні таблиці є прикладами клітинних автоматів.

Машина фон Неймана – це машина Тьюринга, що здатна відтворювати сама себе. У 1950 році фон Нейману вдалося реалізувати цю машину на просторі з 200 000 клітин, кожна з яких могла знаходитися у 29 станах. Правила переходу кожної клітини з одного стану в інший залежали від станів чотирьох сусідніх клітин. Після створення першої машини фон Неймана вдалося створити її значно простіші реалізації (що вимагають меншої кількості комірок і меншої кількості станів). Якоюсь мірою, спрощення машини фон Неймана стало однією з інтелектуальних вправ для кібернетиків. У розвиток цієї роботи й була створена описувана тут гра. Вона, звичайно, не реалізує машину фон Неймана, але є способом вивчення властивостей клітинних автоматів, що керовані простими правилами.

Математик Джон Конвей в 1970 році опублікував у журналі Scientific American (в рубриці «Математичні ігри», яку вів відомий популяризатор Мартін Гарднер) опис гри «Життя». Її правила надзвичайно прості (і цим, зокрема, визначається її привабливість).

Гра реалізується на площині, що складається з квадратних комірок. Кожна комірка має вісім сусідів (рахуючи тих, з якими вона стикається куточками). Кожна комірка може знаходиться у двох станах: «живому» (зайнятому, зазвичай показують чорним кольором) і «мертвому» (вільному, білому). Для запуску гри треба створити початкову конфігурацію («перше покоління»).

Кожне наступне покоління визначається попереднім з урахуванням двох правил:
– «мертва» клітина, що має трьох «живих» сусідів, стає «живою»;
– «жива» клітина, що має менше двох або більше трьох «живих» сусідів, стає «мертвою».

Обчислювати наступні покоління має сенс, поки на полі залишаються «живі» клітини або поки система не входить в цикл, повторюючи один зі своїх попередніх станів.
Вказаних правил досить для породження безлічі патернів (фігур), які демонструють складну поведінку. Багато конструкцій з клітин швидко деградують. Деякі виявляються стійкими (як, наприклад, квадрат з чотирьох сусідніх клітин). Існують «планери» («gliders») – патерни, здатні циклічно змінювати свою конфігурацію, необмежено переміщаючись по площині.

Спочатку Конвей припускав, що патерн, здатний забезпечувати необмежене продовження гри та нескінченне збільшення кількості живих клітин (природно, при використанні нескінченної площини для гри) в цій грі неможливий. Конвей не міг довести це твердження і запропонував премію за його доказ або спростування. Премію отримала група хакерів під керівництвом Білла Госпера: вони витратили півтора роки, намагаючись створити патерн, який відтворював би сам себе, породжуючи при цьому інші фігури. На жаргоні, що застосовується для опису гри «Життя», мова йде про створення «гармати», що стріляє «планерами».

«Планерна гармата Госпера» стала першим патерном, що здатний існувати необмежено довго і породжувати необмежену кількість «живих» клітин.

Звичайно, особливої ​​необхідності реалізовувати гру «Життя» засобами LO Calc немає: існує безліч її хороших реалізацій. Наприклад, на цьому сайті можна як випробувати будь-які свої початкові конфігурації, так і побачити безліч фігур, що мають свої назви, в тому числі – «гармату Госпера», «Gosper gun». Однак, оскільки для вирішення біологічних проблем може бути корисним використання клітинних автоматів, створених засобами LO Calc, принципи створення таких моделей ми обговоримо на прикладі гри «Життя» (рис. 9.1).

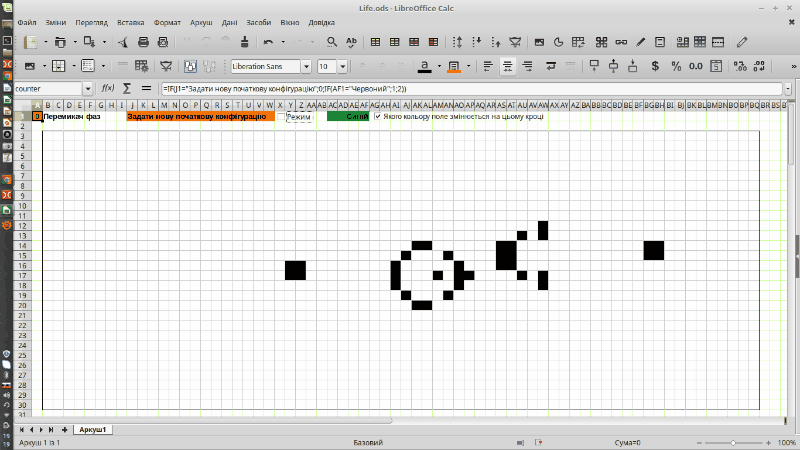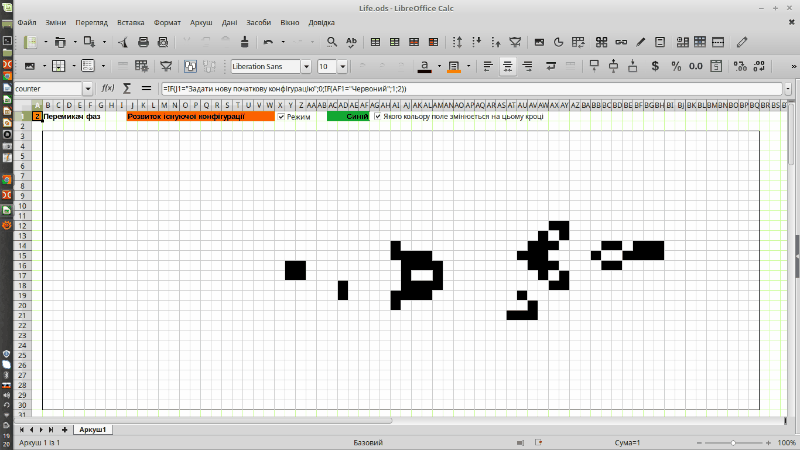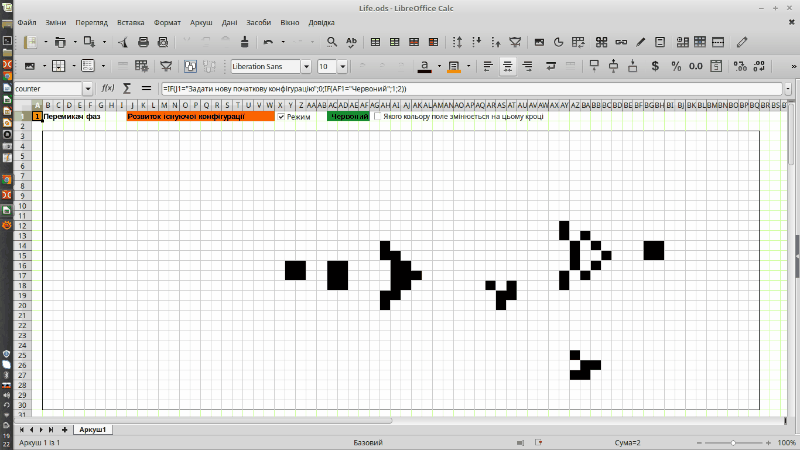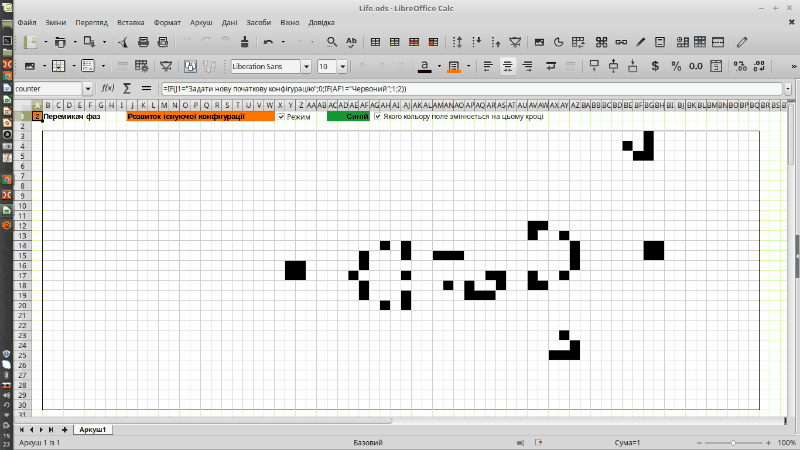
Рис. 9.1. «Планерна гармата Госпера» в реалізації гри Конвея «Життя», що виконана в LO Calc (це анімований gif, що почне рухатися після свого повного завантаження) 

9.2. Реалізація гри «Життя» в LO Calc

Розглянемо приклад реалізації гри «Життя», виконаний в LO Calc. Його можна завантажити, але краще зробити самостійно.

Зрозуміло, реалізувати в LO Calc гру «Життя» можна було багатьма різними способами. Більшість програмних засобів для реалізації цієї гри обходиться одним-єдиним полем. Комірки цього поля спочатку запам'ятовують початкову конфігурацію, а потім крок за кроком її перебудовують. Ці ж комірки демонструють користувачу свій стан завдяки змінам свого кольору.

Ми реалізуємо інший варіант: побудуємо чотири різні поля. Перше буде «екраном», що відбиватиме стан гри; друге слугуватиме для запису початкової конфігурації; третє та четверте по черзі будуть забезпечувати перебудову патерну, який створює гра (рис. 9.2). Крім того, що це рішення значно спрощує формули, що доводиться використовувати, його наслідком є те, що простішим стає аналіз, чому модель поводитися тим або іншим чином. На кожному етапі можна подивитися на початкову конфігурацію, що відбита на жовтому полі, та порівняти два послідовні кроки моделі (на синьому та червоному або, навпаки, червоному та синьому полях).   

Рис. 9.2. Модель з «висоти пташиного польоту». Позначено використання чотирьох різних полів, що мають однакову конфігурацію та посилаються одне на одне

Перш за все, модель може працювати у двох режимах: задання початкової конфігурації та розвитку конфігурації, що існує. Перемикання цих режимів забезпечує перемикач, що розташовано у комірці X1 (рис. 9.3). Безпосередньо «Перемикач», що знаходиться у меню «Елементи керування», має дещо інші функції; в обговорюваній моделі застосовано «Поле з відміткою», де можна знімати та ставити «галочку», переходячи між двома режимами. Залежно від стану цього перемикача (ми будемо, все одно, називати його так) у надпису на червоному тлі змінюється позначення реалізованого режиму.

Завдання-головоломка № 1. Як зроблено так, що залежно від значення перемикача режимів змінюється значення поля на червоному тлі (J1)? Цією коміркою керує «Поле з відміткою», що розташовано в X1.

У режимі розвитку існуючої конфігурації слід, крок за кроком, перебудовувати червоне поле залежно від синього, а потім – синє залежно від червоного. Для цього слугує друге «Поле з відміткою», – перемикач полів. Він керує коміркою AF1. Таким чином, модель може перебувати в одному з трьох станів: завдання навчальної конфігурації, перебудови червоного поля та перебудови синього поля. Вибір, у якому стані перебуває модель, дозволяє перемикач фаз (counter), що розташовано у комірці A1. Формула, що задана в ньому, проста: =IF(J1="Задати нову початкову конфігурацію";0;IF(AF1="Червоний";1;2)). Ви ж розумієте, що двійні лапки маркують текстові значення комірок, на які дається посилання?

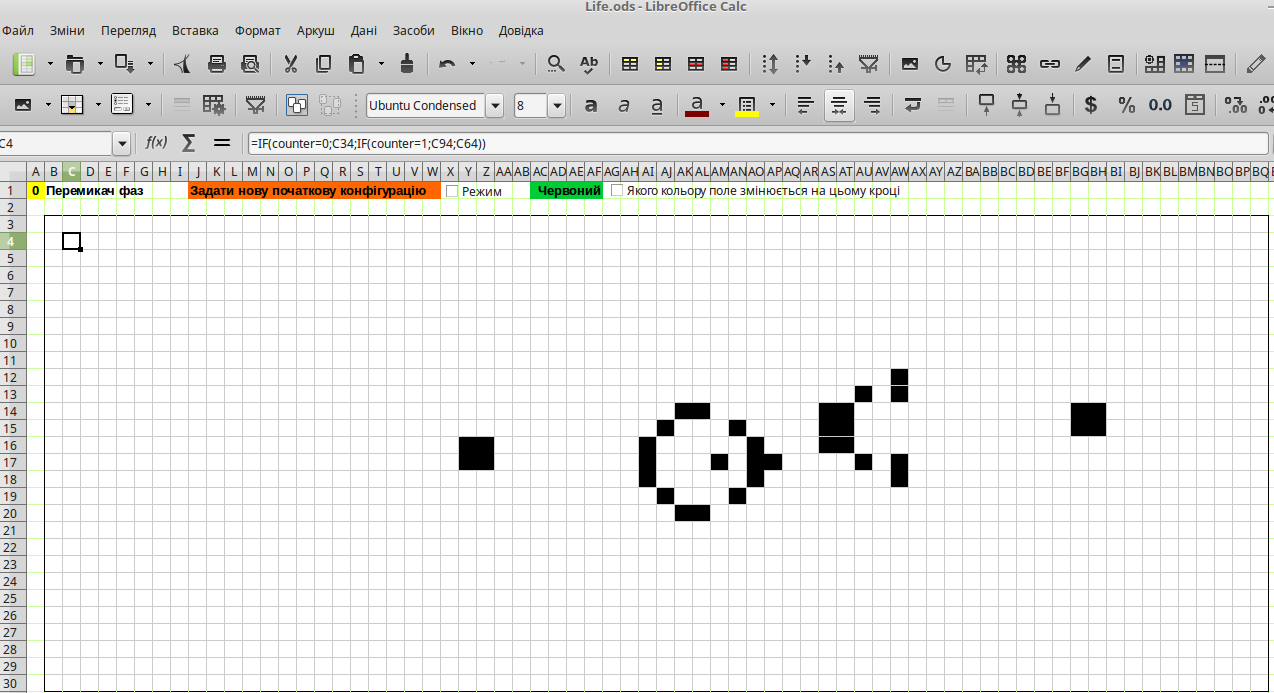
Рис. 9.3. Біле поле є головним; на ньому відбивається нагальний стан гри

Комірки білого поля відбивають стан комірок жовтого поля у разі, якщо перемикач фаз перебуває у стані 0, стан комірок червоного поля у на фазі 1 та синього поля – на фазі 2. Наприклад, для комірки B3 формула має такий вигляд: =IF(counter=0;B33;IF(counter=1;B93;B63)).

Завдання-головоломка № 2. Як зроблено так, що комірки білого поля B3:BQ30 (рис. 9.3) чисто білі у разі значення 0, та чисто чорні у разі значення 1?

Працювати з жовтим полем нескладно. Значення його комірок слід змінювати вручну, з 0 та 1 або навпаки. Умовне форматування зафарбовує нулі жовтим, а одиниці – зеленим (рис. 9.4).

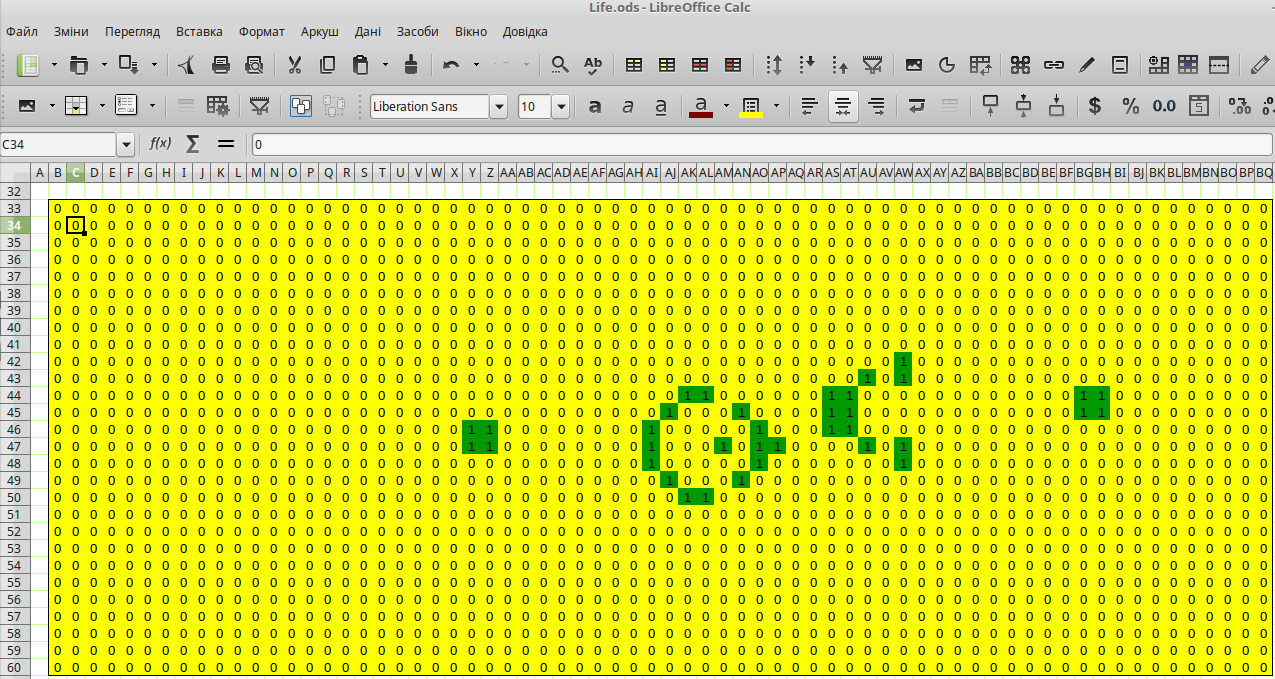
Рис. 9.4. На жовтому полі можна задати початкову конфігурацію (перемикач фаз має перебувати у стані 0)

Синє та червоне поля є «близнюками» – кожне з них у режимі розвитку існуючої конфігурації по черзі перебудовується залежно від патерну на іншому полі. Розглянемо формулу комірки C64, яку показано на рис. 9.5: =IF(counter=0;C34;IF(counter=1;C64;IF(counter=2;IF(C94=0;IF((B93+C93+D93+D94+D95+C95+B95+B94)=3;1;0);
IF((B93+C93+D93+D94+D95+C95+B95+B94)>3;0;IF((B93+C93+D93+D94+D95+C95+B95+B94)<2;0;1)));C94)))

Щоб зрозуміти цю формулу, слід врахувати, що «відбиттям» комірки C64 (на синьому полі) є комірка C94 (на червоному полі). Комірки B93, C93, D93, D94, D95, C95, B95 та B94 є сусідами цієї комірки. Як ви пам'ятаєте, комірка залишиться «живою» лише у разі, якщо буде мати 3 «живих» сусіда.

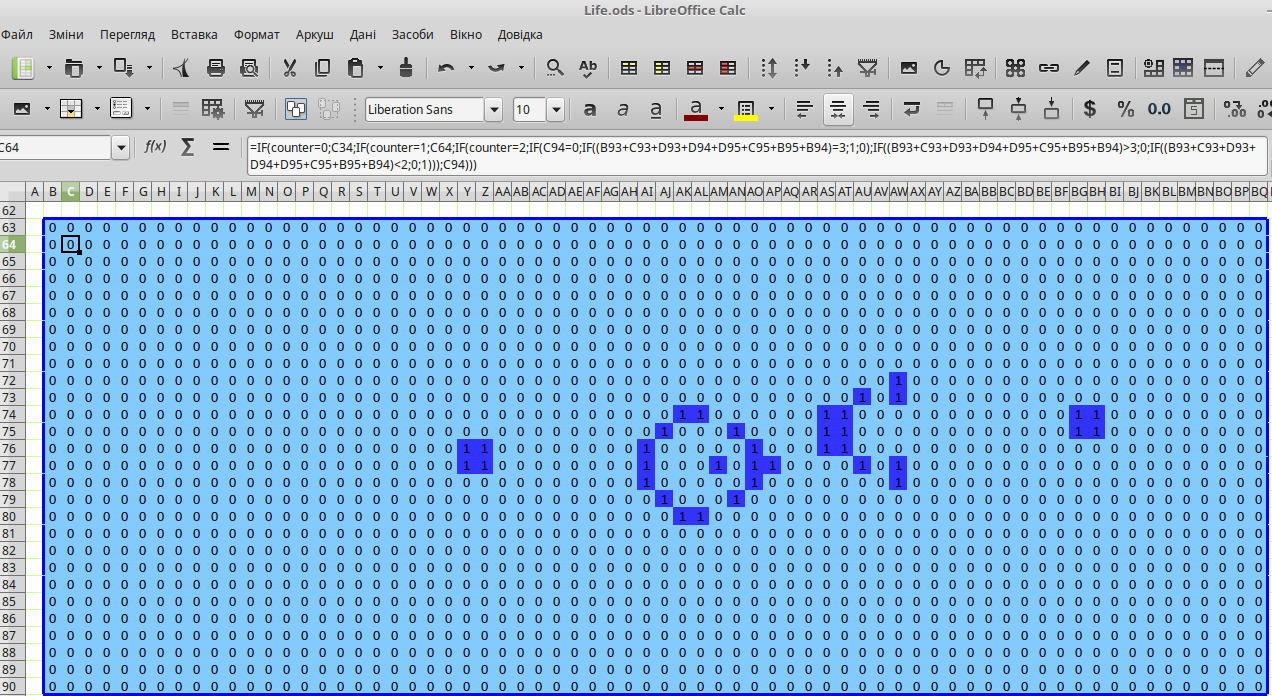
Рис. 9.5. Синє поле перебудовується, коли перемикач фаз має значення 2

Комірка B63 має дещо іншу формулу: =IF(counter=0;B33;IF(counter=1;B63;IF(counter=2;IF(B93=0;IF((BQ120+B120+C120+C93+C94+B94+BQ94+BQ93)=3;1;0);
IF((BQ120+B120+C120+C93+C94+B94+BQ94+BQ93)>3;0;IF((BQ120+B120+C120+C93+C94+B94+BQ94+BQ93)<2;0;1)));B93)))

Це пов'язано з тим, що поле гри «Життя» є безкінечним. З коміркою B93, що розташована у куті, межує комірка BQ120, розташована у протилежному куті, а також BQ93, розташована з іншого боку по горизонталі, та B120, розташована з іншого боку по вертикалі – впевніться в цьому самі за допомогою рис. 9.6!

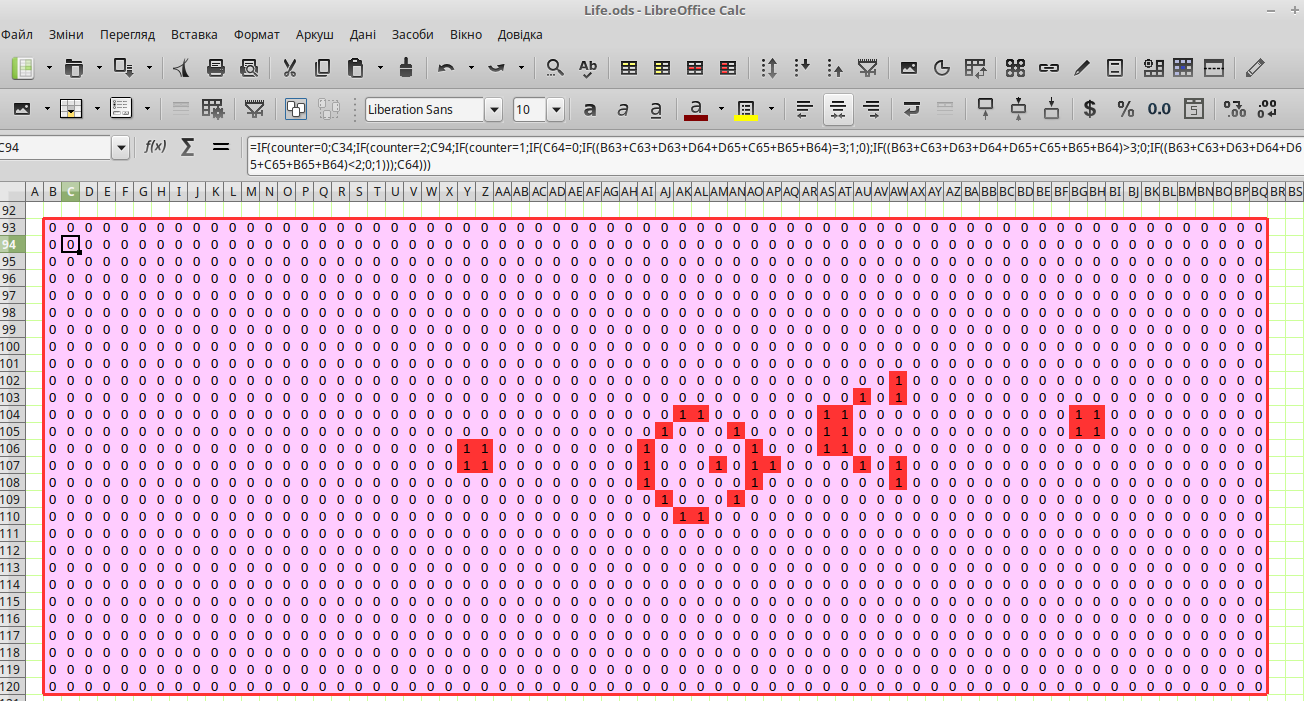
Рис. 9.6. Червоне поле перебудовується, коли перемикач фаз має значення 1

Таким чином, користування моделлю є нескладним. Перемикаєте режим, щоб задати нову конфігурацію; знову перемикаєте режим та починаєте «клацати» перемикачем, що обирає змінювані поля. Крок за кроком спостерігаєте зміни «Життя»...

...і не забудте знайти відповіді на завдання-головоломки!