| ← | → | |
| Ускладнення моделі: імітація логістичного зростання | Врахування демографічної структури: «Модель трьох поколінь» | Різні способи імітації обмежень популяційного зростання |
| Сотворіння світів-03 | Сотворіння світів-04 | Сотворіння світів-05 |
4. Врахування демографічної структури: «Модель трьох поколінь»
4.1. Нові можливості
Моделі, що описують експоненційне і логістичне зростання, які ми розглядали на минулих етапах нашого курсу, залишаються надзвичайно умовними, відірваними від дійсності. Фактично, ми адаптували аналітичні залежності до покрокового розрахунку за допомогою різницевих рівнянь (рівнянь, що вираховують різницю між значенням певної величини на попередньому та наступному кроках). Ми не використали в повному масштабі ключову перевагу імітаційних моделей — можливість послідовного моделювання різних процесів, що відбуваються в системі-оригіналі на кожному циклі її динаміки. Спробуємо виправити це упущення.
Для початку зробимо якомога простішу модель. Задамо в ній дві статі, три покоління і смертність в результаті конкуренції, коли чисельність перевищує ємність середовища (це не логістичне зростання, а експоненційне, який «обрізається» кожен раз, коли ємність середовища перевищує чисельність модельної популяції). Цю модель не слід вважати остаточною, але її створення дозволить нам розглянути деякі важливі принципи побудови імітаційних моделей. Побудуємо цю модель так, щоб на її прикладі показати певний шаблон розміщення моделі на аркуші LO Calc. Умовно позначимо цей шаблон «Таблиця з шапкою». Починаючи з цієї моделі, ми будемо дотримуватися стилю позначень, який можна назвати «рекомендованим» (в даному курсі), в усякому разі, для популяційно-екологічних моделей. Список позначень, які використовуються в таких моделях, наведено тут. Крім того, при створенні цієї моделі використовуємо дві можливості, які ми ще не застосовували. Це використання імен комірок та смуг прокрутки для керування вхідними параметрами.
Почнемо з того, що подивимось на зовнішній вигляд реалізації моделі (рис. 4.1), а далі обговоримо її створення.
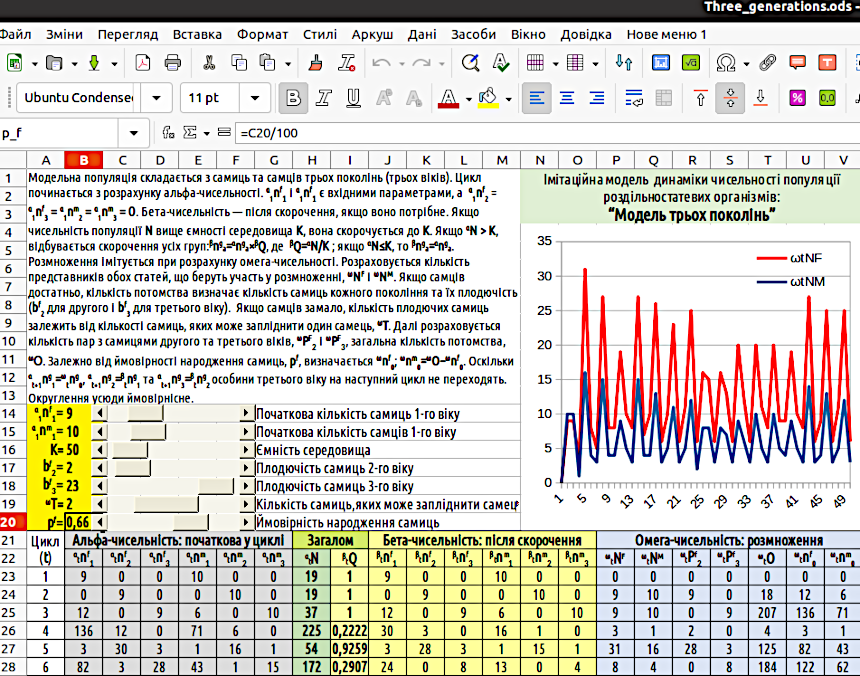
Рис. 4.1. Загальний вигляд реалізації «Моделі трьох поколінь»
На рис. 4.1. ми бачимо наступні елементи: назву (N1:V3); інформаційне поле з описом моделі (A1:M13); зону керування початковими параметрами (A14:M20); зону виводу результатів моделювання (N4:V20) та зону розрахунків (A21:V...?). Як ви зрозуміли, положення кожної зони позначено так, як в електронних таблицях позначають прямокутні ділянки: через координати лівого верхнього та правого нижнього кутів.
В описі моделі застосовано «рекомендований» стиль позначень. Він є таким: етапциклпоказникформавік. Пояснимо, що мається на увазі під цими поняттями:
— показник: власне позначення тієї величини, що мається на увазі; припустимо, чисельність групи позначається n, а загальна чисельність певної сукупності груп — N;
— етап: частина циклу; кожен цикл розбивається на необхідну кількість етапів перетворення, що позначаються грецькими літерами (надрядковими позначками ліворуч); згідно з цією логікою, цикл можна представити як сукупність перетворень αtN → βtN → γtN → δtN → εtN → … → ωtN;
— цикл: повторювана у ході роботи послідовність перетворювань, що може, наприклад, відповідати річному циклу у житті певної популяції; позначається номером у підрядковій позначці ліворуч, а в узагальненому вигляді (як у прикладі з позначеннями етапів) — буквою t;
— форма: генотипи, статі чи інші категорії особин; позначаються надрядковою позначкою праворуч, наприклад, в обговорюваній моделі — F (females) або M (males); в узагальненому вигляді можна використовувати позначку g (genotypes);
— вік: особини певної форми можуть мати різний вік; групу утворюють особини однієї форми та одного віку; вік позначається цифрою в підрядковій позначці праворуч; в узагальненому вигляді використовується позначка a (age).
Коротко цю форму записи можна позначити так: α→ωtZga. Тут α→ω — грецькі літери, що позначають етапи, t — номер циклу імітації і розрахунків, Z — показник, що ми розглядаємо, g — генотип, стать форма або інша категорія особин та a — вік.
Ви зрозуміли, чому на рис. 4.1 в заголовках таблиці в позначенні кількості статевозрілих самиць ωtNF буква F — велика, а в позначенні кількості пар, до яких входять самиці другого віку ωtPf2 буква f — мала? Звісно, це не сама принципова обставина, але вона допомагає зрозуміти особливості стилю позначень. Коли мова йде про кількість самиць, маються на увазі особини двох груп: самиці-дворічки та самиці-трирічки. Коли йде мова про кількість пар, куди входять самиці-дворічки, вони належать до однієї-єдиної групи. У першому разі буква F позначає категорію, що включає більше, ніж одну групу, у другому — буква f позначає одну групу.
Тепер ви зможете зрозуміти опис моделі. Він є таким:
Модельна популяція складається з самиць та самців трьох поколінь (трьох віків). Цикл починається з розрахунку альфа-чисельності. α1nf1 і α1nf1 є вхідними параметрами, а α1nf2 = α1nf3 = α1nm2 = α1nm3 = 0. Бета-чисельність — після скорочення, якщо воно потрібне. Якщо чисельність популяції N вище ємності середовища К, вона скорочується до К. Якщо αN > K, відбувається скорочення усіх груп: βnga=αnga ×βQ, де βQ=αN/K; якщо αN≤K, то βnga=αnfa. Розмноження імітується при розрахунку омега-чисельності. Розраховується кількість представників обох статей, ωNF і ωNM. Якщо самців достатньо, кількість потомства визначає кількість самиць кожного покоління та їх плодючість (bf2 для другого і bf3 для третього віку). Якщо самців замало, кількість плодючих самиць залежить від кількості самиць, яких може запліднити один самець, ωT. Далі розраховується кількість пар з самицями другого та третього віків, ωPF2 і ωPF3, загальна кількість потомства, ωO. Залежно від ймовірності народження самиць, pf, визначається ωnf0; ωnm0=ωO−ωnf0. Оскільки αt+1ng1=ωtng0, αt+1ng2=βtng1 та αt+1ng3=βtng2, особини третього віку на наступний цикл не переходять. Округлення усюди ймовірнісне.
Побудову моделі розпочнемо з розгляду використання іменованих комірок. Насправді обговорювана модель є настільки нескладною, що без окремих імен для вхідних параметрів можна було б легко обійтися. Але на її прикладі ми маємо засвоїти шаблон, який може використовуватися і для складніших моделей. Якщо ви побудуєте достатньо складну модель, одна з проблем при роботі з нею полягатиме у написанні та, що є складнішим, у перевірці формул. Досить часто ці формули займають кілька рядків... Як розібратися в них? Використовувати окремі імена для вхідних параметрів! Це значно поліпшить сприйняття формул...
Як ви бачите на рис. 4.1, в моделі наочно задається 7 вхідних параметрів (насправді, є ще 4 параметри — початкові чисельності дворічок та трирічок, але ми їх задаємо за умовчанням рівними 0). Кожній з 7 комірок, що містять початкові параметри, надані свої імена. Щоб задати ім'я комірці, треба її виділити, а після пройти шляхом «Аркуш / Названі діапазони та вирази / Задати...». Деякі сполучення символів використовувати в якості імені не можна (наприклад, ім'я не може збігатися з позначенням будь-якої іншої комірки, тобто не може бути комбінація літери і номера). Комірку можна назвати однією літерою, але не будь-якою; ім'я U буде прийнято, а ім'я T — ні В іменах символів можна використовувати підкреслення (_).
Щоб подивитися на усю сукупність імен та редагувати її, можна відкрити окреме вікно. Воно відкриється, якщо пройти шляхом «Аркуш / Названі діапазони та вирази / Керування назвами...», а також якщо розгорнути меню, що розташовано поруч з полем у лівому верхньому куті листа LO Calc, де вказується адреса комірки. Якщо ви оберете опцію «Керування назвами...», ви ввійдете у діалог, де зможете задавати, змінювати та видаляти імена окремих комірок (рис. 4.2).
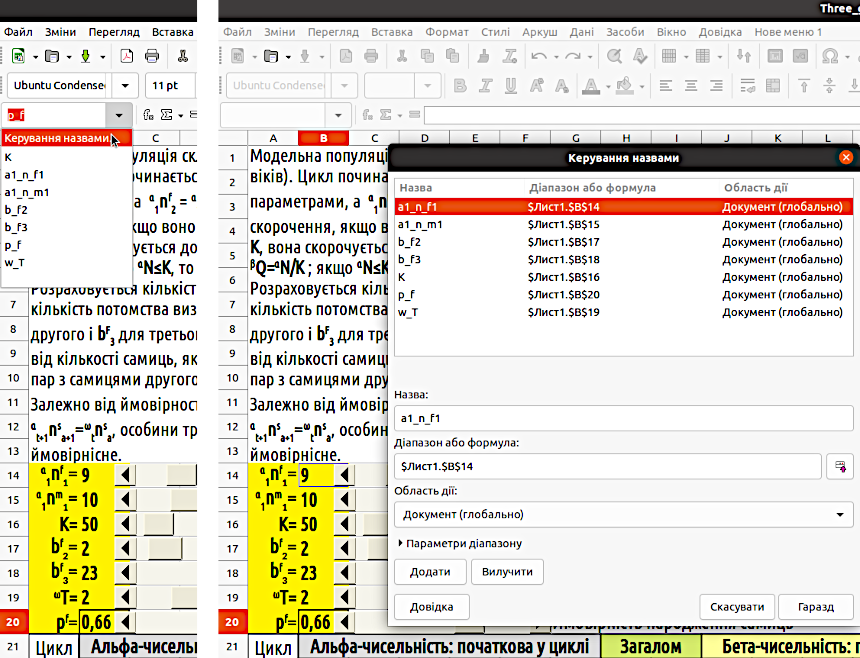
Рис. 4.2. Іменування комірок. Ліворуч показано, де треба викликати діалог «Керування назвами...». Праворуч — такий діалог для моделі, яку ми будемо зараз будувати
Тепер, щоб вставити у формулу посилання на комірку B16, достатньо буде просто написати K. Це посилання абсолютне, не змінюється при розтягуванні, копіюванні та переміщенні комірок.
Під час роботи з моделлю дуже корисно, коли вхідні параметри будуть показані максимально наочно, а їх зміни реалізовані максимально зручно. Цьому може сприяти використання смуг прокрутки. Це один з різновидів елементів управління, передбачених електронними таблицями. Найпростіший спосіб вставити в файл смугу прокрутки — скопіювати її з того файлу, де вона вже є. Складніший (але більш правильний) спосіб такий. Пройдіть по шляху «Перегляд / Панелі інструментів» і оберіть панель «Елементи керування». На аркуші LO Calc з'явиться ця панель. Перейдіть в режим розробки за допомогою кнопки «Режим розробки» (рис. 4.2). Вам стануть доступні елементи управління, серед яких можна вибрати смугу прокрутки (рис. 4.3). Вибравши її, окресліть якийсь простір на аркуші; LO Calc вставить туди цей елемент управління. Залежно від того, який простір ви окреслите для цього елементу, він буде горизонтальним або вертикальним.
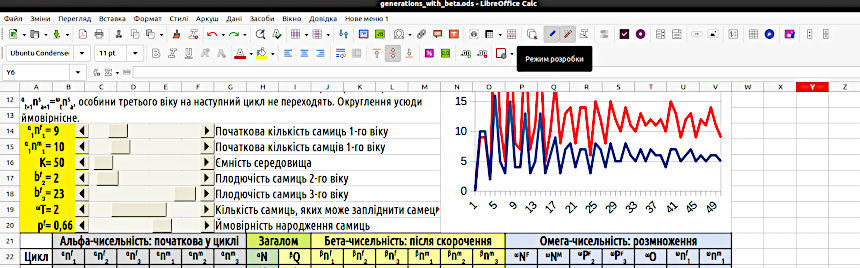
Рис. 4.3. Тут показано фрагмент налаштованої панелі інструментів LO Calc, у яку входить і панель «Елементи керування». У різних версіях LO Calc кнопка «Режим розробки» може мати різний вигляд. У будь-якому разі, важливо слідкувати, натиснута вона або ні
Коли режим розробки ввімкнено, ви можете розміщувати на аркуші елементи керування та змінювати їх властивості. Втім, в цьому режимі ці елементи не працюють. Після того, як ви облаштуєте усе, як треба, слід вийти з режиму розробки; елементи керування «запрацюють». Оберіть смугу прокрутки (рис. 4.4).

Рис. 4.4. Тепер можна обрати смугу прокрутки, поставити її на лист LO Calc та налаштувати
Якщо панель інструментів активна, а кнопки «Смуга прокрутки» в ній нема, пройдіть шляхом «Засоби / Налаштувати...» та налаштуйте, які саме меню і які кнопки ви бажаєте бачити на вашому екрані (рис. 4.5)
Рис. 4.5. Налаштування панелей інструментів
Щоб розмістити смугу прокрутки на аркуші, слід обрати цей елемент керування на панелі та «розтягнути» курсором зону, де він має бути розташованим. Це можливо зробити лише у режимі розробки. Після того, як ви розмістите смугу, стане активною кнопка «Властивості елементу керування» (крім того, цей режим можна вибрати через меню правої кнопки миші). Ви потрапите в діалог «Властивості: Смуга прокрутки». Цей діалог відкриється на другій вкладці, «Дані»; там слід вказати ту комірку, значення в якій буде змінюватися за допомогою цієї смуги прокрутки (рис. 4.6).
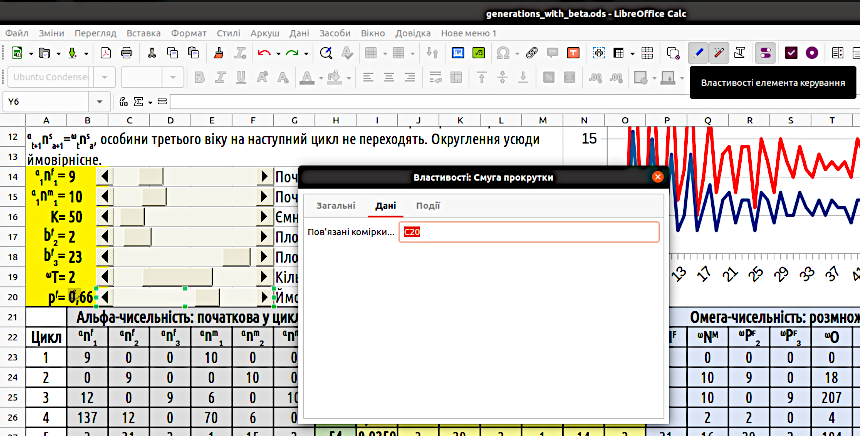
Рис. 4.6. Налаштування останньої смуги прокрутки (її виділено зеленими маркерами). Зверніть увагу: смуга керує коміркою у стовпці C; комірка у стовпці B, що задає вхідний параметр, залежить від цієї комірки
На першій вкладці, «Загальні», можна налаштувати властивості смуги, в число яких входять розміри, положення, мінімальне і максимальне значення, що задаються за допомогою цієї смуги, крок зміни, її розташування і розміри тощо (рис. 4.7). Якщо вам здається, що підгонка смуг прокрутки та інші подібні дії є зайвими красотами, ви помиляєтеся. Увага до деталей дозволяє робити моделі, які легко інтерпретувати та де відносно мало помилок...
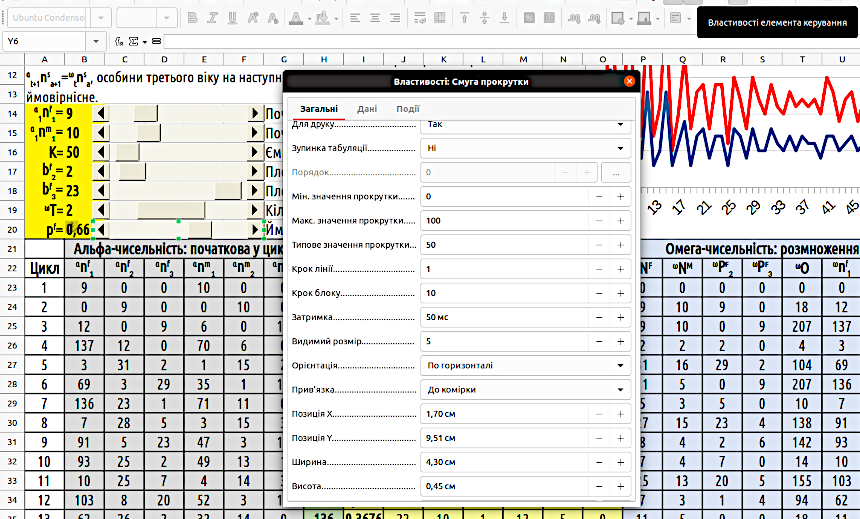
Рис. 4.7. В цьому діалозі можна гнучко налаштувати усі властивості смуг прокрутки. До речі, як ви думаєте, як автор добився такого акуратного розташування смуг прокрутки, як на цьому скріні?
Після того, як властивості елементу керування налаштовані, вікно діалогу можна просто закрити: зміни будуть збережені. Зверніть увагу: смуга прокрутки запрацює лише тоді, коли ви вийдете з режиму розробки! Щоб змінити розташування смуги або її інші властивості, треба буде знову входити у режим розробки.
Як ви вже зрозуміли, в тій моделі, що ви будете зараз створювати, коміркам з початковими параметрами слід надати імена та зв'язати з ними смуги прокрутки, щоб змінювати значення цих параметрів найзручнішим образом. На скрині екрану ви бачите 7 смуг прокрутки; 6 з них змінюють комірки у стовпці B, а остання — у стовпці C (рис. 4.6). Річ у тім. що за допомогою смуг прокрутки не можна задавати нецілі значення. Остання смуга змінює значення комірки у діапазоні від 0 до 100. Як ви можете побачити на рис. 4.1 (зверніть увагу на адресу комірки та формулу, що в ній стоїть!), комірка B20 розраховується на підставі значення комірки C20. Сама ж комірка C20 схована під смугою прокрутки, щоб не заважати користувачу моделі.
4.2. Розрахунки в «Моделі трьох поколінь»
У попередньому пункті ми описали особливості реалізації «Моделі трьох поколінь». Тут слід обговорити, як побудована концептуальна модель, реалізацію якої ми розглянули. Нам слід розглянути, які зв'язки поєднують величини, які ми розглядаємо в цій моделі.
Ми змінюємо 7 вхідних параметрів, яким (рис. 4.2) привласнені імена (зверху донизу): a1_n_f1, a1_n_m1, K, b_f2, b_f3, w_T і p_f.
Візуалізація вихідних даних представлена звичайним графіком, який ви вже вмієте будувати, а структуру поля для розрахунків ми зараз детально проаналізуємо. Як ви можете побачити на скринах, розрахунки починаються з 23 рядку. Щоб проілюструвати обговорення, ми розглянемо скрини моделі, де показані не значення комірок, а формули, що в них містяться (рис. 4.8 та рис. 4.9). Щоб перейти у такий режим, слід віддати команди «Перегляд / Показати формулу».
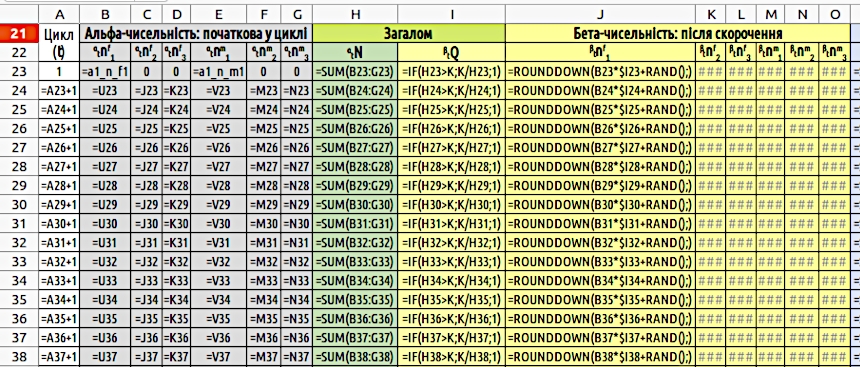
Рис. 4.8. Формули в першій частині «Моделі трьох поколінь». Розрахунки бета-чисельностей є однотипними і показані лише для першого стовпця
У стовпці A представлені цикли роботи моделі (що у дійсності можуть відповідати, наприклад, рокам). Перший рядок у зоні розрахунків — нульовий, A23{1}. Друга комірка цього стовпця, A24, як і усі наступні комірки («розтягнуті» з A24), містять найпростіший лічильник: A24{=A23+1}.
У стовпці B вказується чисельність самиць першого року на початку циклу — αtnf1. Формули в комірках такі: B23{=a1_n_f1}, B24{=U23}; всі наступні комірки цього стовпчика отримані з B24 «розтягуванням». Сенс цієї різниці простий. В комірці U23 вказана кількість самиць у потомстві, яке могло з'явитися на попередньому кроці моделі. Те, що на першому циклі в моделі потомства нема, не так важливо; якби на першому циклі були б придатні для розмноження особини, було б і потомство. Ми задаємо в цих комірках формули, які можемо «розтягнути» на усю модель.
У стовпці C вказується чисельність самиць другого віку на початку циклу — αtnf2. Формули в осередках такі: С23{0} (за умовами всі особини на початку роботи моделі належать до першого віку), С24{=J23}; всі наступні комірки стовпчика отримані з С24 «розтягуванням». В комірці J23 вказується чисельність самиць першого віку, які лишилися після скорочення чисельності рік тому. Тепер вони досягли другого віку. Аналогічні формули введені в стовпець D, де вказується чисельність самиць третього року — αtnf3.
Як ви можете зрозуміти (і перевірити себе за рис. 4.8), формули у стовпцях E, F і G є аналогічними формулам у стовпцях B, C і D.
Рухаємося далі. У стовпці H, αtN, розраховується загальна чисельність всіх особин; H23{=SUM(B23:G23)}, нижче — «розтягнути». В цьому і наступних стовпцях різниця між комірками першого та другого циклів роботи моделі зникає, адже так легше її будувати. Функцію SUM ми ще не розглядали, але її застосування є інтуїтивно зрозумілим і не потребує багатослівних пояснень.
У стовпчику I розраховується коефіцієнт скорочення, який застосовується для усіх груп. Його не можна розрахувати, просто розділив ємність середовища на загальну чисельність (якби ми так зробили, у разі, якщо чисельність особин була б меншою за ємність середовища, вона б чудовим чином збільшувалася б). Тому тут необхідна конструкція з умовою: I23{=IF(H23>K;K/H23;1)}.
Стовпці J — O містять розрахунок бета-чисельності усіх груп. В першому з них в першому рядку стоїть формула J23{=ROUNDDOWN(B23*$I23+RAND();)}, усі інші є аналогічними. Як ви розумієте, при скороченні чисельності могли б з'являтися нецілі числа; як вказано в описі моделі, в ній застосовується ймовірнісне округлення за допомогою функцій ROUNDDOWN і RAND, як це описувалося в пункті 3.5.
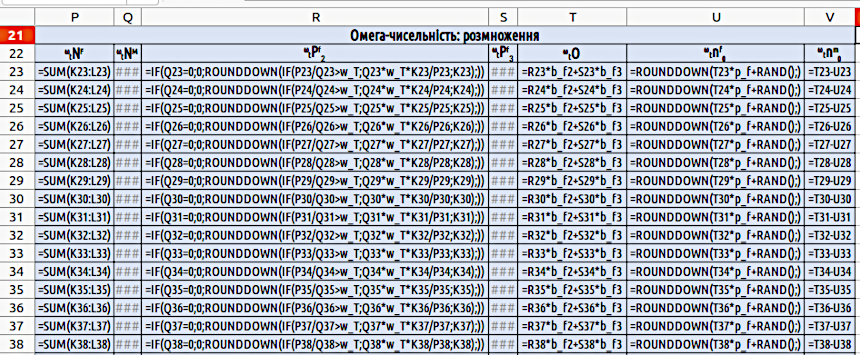
Рис. 4.9. Формули в другій частині «Моделі трьох поколінь». Розрахунки кількості самців однотипні з розрахунками кількості самиць; кількість пар з самицями третього віку розраховуються аналогічно до чисельності пар з самицями другого віку
У стовпчиках P і Q відбувається обчислення загальної кількості статевозрілих самиць і самців, ωtNF і ωtNM відповідно. Формули є дуже простими: P23{=SUM(K23:L23)}; в комірці Q23 формула є аналогічною. Зрозуміло, що в цих комірках складається чисельність статевозрілих самок і самців різного віку.
У стовпчиках R і S обчислюється кількість пар з самицями другого і третього віку, ωtPf2 і ωtPf3 відповідно. Слід передбачити, що самців може не вистачити на всіх самиць, і обчислення необхідно проводити так: R23{=IF(Q23=0;0;ROUNDDOWN(IF(P23/Q23>w_T;Q23*w_T*K23/P23;K23);))}. Перша з функцій IF оберігає від ділення на 0, оскільки далі необхідно ділити чисельність самиць на чисельність самців. Якщо самців в популяції немає, то і пар немає. Якщо самці є, то треба визначити, чи достатня їх чисельність для того, щоб вони покрили всіх самиць. Якщо відношення числа самиць до числа самців менше величини ωT, то чисельність пар з самицями другого віку дорівнює чисельності самиць другого віку, а чисельність пар з самицями третього віку дорівнює чисельності самиць третього віку. Якщо самців бракує (треба сказати, що при передбачених в моделі умовах це може відбутися тільки на найпершому етапі, якщо задати надлишок самиць і недолік самців), то чисельність пар з самицями обох вікових груп скорочується пропорційно наявної кількості самців: кількість_самців*T*кількість_самиць_відповідного_віку/кількість_самиць, або для самиць другого віку на першому циклі роботи моделі Q23*w_T*K23/P23.
В стовпці T обчислюється кількість потомства (цю кількість позначено ωO, від англійського offspring). Для цього до добутку кількості пар з самицями другого віку і плодючості самиць другого віку слід додати добуток кількості пар з самицями третього віку і плодючості самиць третього віку: T23{=R23*b_f2+S23*b_f3}.
Стовпець U містить обчислення кількості самиць, що з'являються у потомстві. Для їх розрахунку слід врахувати їх очікувану частку у потомстві pf, що входить до початкових параметрів, та застосувати ймовірнісне округлення: U23{=ROUNDDOWN(T23*p_f+RAND();)}. Скільки буде у потомстві самців, встановити дуже просто: V23{=T23-U23}. Всі обчислення циклу закінчені; лишилося «розтягнути» необхідні формули та побудувати графік за даними, що містяться в стовпцях P і Q.
4.3. Поведінка отриманої моделі
Тепер є сенс задуматися про деякі аспекти отриманої моделі. Як видно по її скрину (рис. 4.1), при деяких поєднаннях значень вхідних величин в моделі виникають коливання, які іноді виглядають як «биття». Важливо зрозуміти, що є їх причиною. Які поєднання вхідних коефіцієнтів породжують ці «биття»? Чим відрізняються ситуації в їх мінімумах і максимумах? Чому протягом декількох перших років при показаннях на малюнку вхідних значеннях зростання модельної популяції було повільним, а потім вона зробила «ривок»?
Чи можна обчислити співвідношення, зміна якого викликає «биття» чисельності? Чи можна побудувати графік такої величини? Чи можна накласти графік такої величини на графік динаміки чисельності?
Перевірте, чи пов'язані коливання чисельності модельної популяції з нерівноважним співвідношенням статей? Якщо коливання пов'язані з іншими причинами, можна обрати для вхідного параметра pf значення 0,5 та не змінювати його під час аналізу поведінки моделі.
Які спрощення, прийняті при побудові даної моделі, були найважливішими? Ймовірно, саме серйозне спрощення (тісно пов'язане з причиною биття) полягає в тому, що смертність при перевищенні ємності середовища для всіх вікових класів виявлялася однаковою. Друге серйозне спрощення полягає в тому, що чисельність популяції зростає без будь-якого уповільнення, поки не досягає ємності середовища, а потім рік за роком різко обрізається на цьому рівні.
Виходячи зі сказаного, стає зрозумілим напрям подальшого ускладнення отриманої моделі та наближення її до дійсності. Треба ввести окремі показники смертності (і, можливо, конкурентоспроможності) для різних вікових класів (і, ймовірно, різної статі). Треба ускладнити механізм конкурентного скорочення чисельності.
Програма подальших дій починає вимальовуватися... Втім, перш за все, слід дати відповідь на поставлене питання: з якими процесами пов'язані періодичні коливання чисельності популяції в побудованій нами моделі з трьома поколіннями?
Перш все, можна переконатися, що ці коливання виявляються тим сильніше, чим більшою буде різниця в плодючості між особинами другого і третього віку. Це можна встановити, просто розглядаючи, як відбиваються на вихідному графіку зміни початкових параметрів. При рівній плодючості двох вікових груп чисельність популяції швидко встановлюється на певному рівні.
А з чим пов'язані коливання чисельності? З періодичною зміною співвідношення між поколіннями. Розглянемо докладніше, як візуалізувати ці зміни, тим більше, що це дасть можливість обговорити найпростіші засоби редагування графіків.
Почнемо з того, що збільшимо ємність середовища. Наслідком стане те, що коливання почнуть згасати. За допомогою моделі можна експериментально впевнитися, що коливання, які почали згасати, можуть посилитися лише у разі невеликої ємності середовища. На підставі цього можна зрозуміти, що причина посилення коливань — відхилення співвідношення поколінь, що пов'язані з процедурою округлення. Чим меншою є чисельність модельної популяції, тим більший вплив на її динаміку може мати випадкові процеси при ймовірнісному округленні.
Введемо в одну з комірок збоку від зони обчислень формули, яку видно на рис. 4.10. Над нею зробимо підпис, що пояснює, що саме ми обчислюємо. Для трьох стовпців, що демонструють динаміку поколінь, побудуємо графік. Розташуємо його прямо над зоною обчислень.
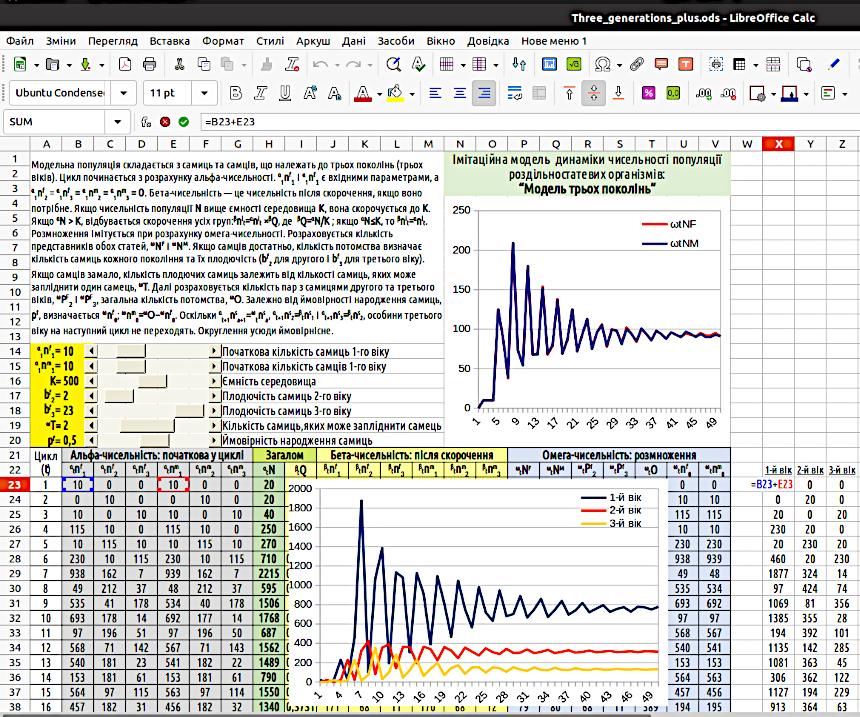
Рис. 4.10. Коливання чисельності модельної популяції є наслідком коливань співвідношення між поколіннями
Причиною «биття» є коливання співвідношення між поколіннями! Коли більш численне покоління переходить у третій вік, це призводить до стрибка чисельності потомства, різкого скорочення чисельності особин усіх віків та формуванню менш численного покоління. Коли воно почне розмножуватися, у модельній популяції зможе лишитися більша кількість потомства; так сформується більш численне покоління... Зазначені циклічні коливання співвідношення поколінь й породжують циклічні «биття» чисельності популяції, що з часом згасають. Згодом чисельність стабілізується, але будь-яке збурення (наприклад, суттєва зміна чисельності популяції в результаті якогось впливу) знову породить «биття» чисельності, які в стабільних умовах з часом згасатимуть.
Цікавий спосіб представлення тих же результатів показано на рис. 4.11, на графіку, що розташовано згори праворуч. Дані стовпчика, що описує частку молодих особин (у процентах від загальної чисельності), відкладені по осі абсцис, а дані про частки трирічних — на осі ординат. Ламана крива описує траєкторію системи в показаному фазовому просторі. Найперша точка — в нижньому правому куті наведеного графіка (100% молодих). Наступна — на початку координат (всі особини — дворічки). На третьому році співвідношення поколінь близько до 50%/50% (особини першого покоління залишили потомство, і на кожну пару батьків довелося, відповідно до показаних на рис. 4.11 параметрів, по двоє нащадків). Побудуйте такий графік самостійно!
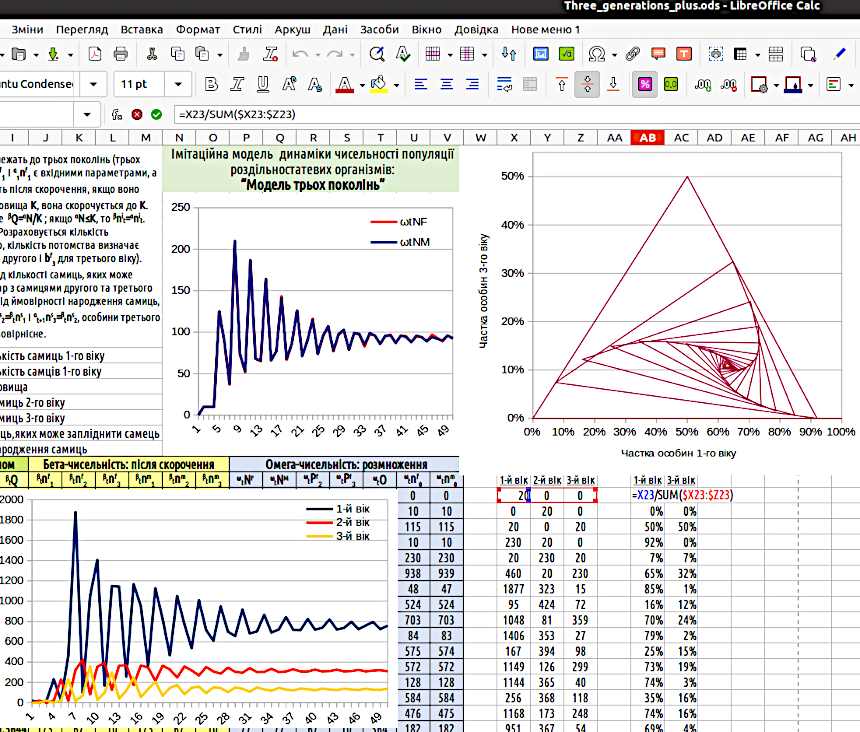
Рис. 4.11. Додано графік, що демонструє траєкторію модельної популяції в фазовому просторі. З кожним кроком модельна система переміщається з одного кута ламаної лінії в наступний. Початок — у правому нижньому куті
Наскільки реалістичним є припущення, що особини різного віку в рівній мірі вичерпують ресурси середовища і мають рівні шанси на виживання в разі конкурентного скорочення чисельності? Швидше за все, це дуже грубе наближення. Досвід катастроф, пов'язаних з нестачею ресурсів (і в популяціях людини, і в популяціях інших видів) свідчать, що деякі групи населення виявляються особливо вразливими. Співвідношення статей і вікових груп у популяції, що пройшла через «голодне» скорочення чисельності, має сильно зсуватися в порівнянні з початковим таким співвідношенням.
4.4. Логіка побудови імітаційної моделі
Спираючись на модель, показану на рис. 4.1, ми можемо обговорити ще одну навчальну проблему. Як будується модель? Спочатку автор моделі розділяє процес, який він вивчає, на певні кроки. Більшість моделей в цьому курсі працюють, багато разів повторюючи певний цикл (наприклад, такий, що відповідає року або ж певному поколінню). Події, що відбуваються на кожному циклі, можна розділити на певні етапи. Наприклад, етапи, що розглядає наша модель — розрахунок α-чисельності на кожному циклі, визначення ω-чисельності (зі скороченням у разі перевищення ємності середовища), утворення пар та ω-чисельності — чисельності потомства. Що, наприклад, впливає на α-чисельність, визначає її значення? Для першого циклу у моделі (його можна вважати нульовим) — початкова чисельність, що задається серед початкових параметрів. Для усіх наступних циклів α-чисельність залежить від ω-чисельності та результату розмноження на попередньому етапі. Сукупність таких зв'язків умовно показано на рис. 4.12.
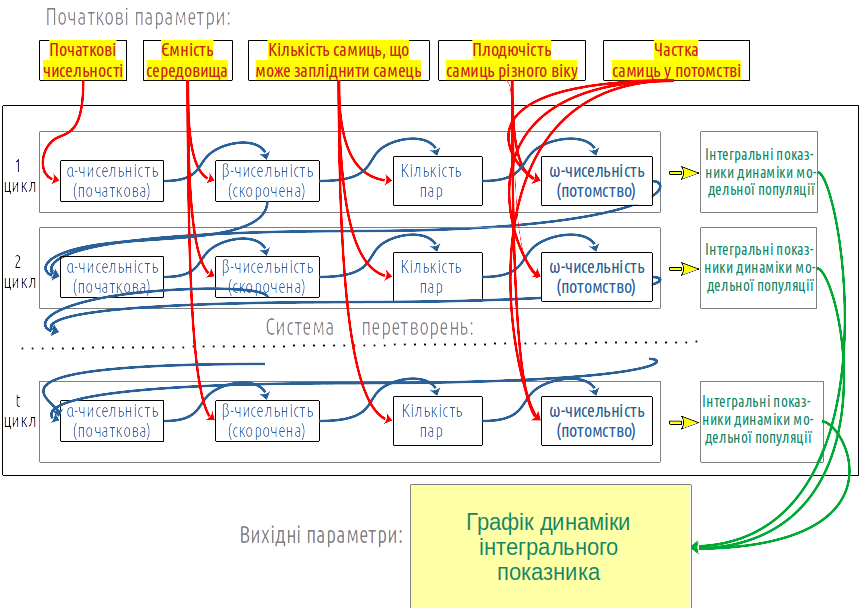
Рис. 4.12. Залежності змінних у моделі показані на цій схемі стрілками. Якщо ми вкажемо формули, що визначають ці залежності, ми отримаємо концептуальну модель. Її можна реалізувати на різній програмній основі
Для розрахунків, що входять у систему перетворень, необхідно визначити початкові параметри. Результатом розрахунків буде певний вихідний результат, наприклад, динаміка певного показника. Інтегральним показником, динаміка якого демонструється на графіку на рис. 4.1, є чисельність статевозрілих самиць та самців.
Якщо ми визначимо, за якими формулами розраховуються усі проміжні та прикінцеві значення, ми створимо концептуально модель. Цю модель можна реалізувати на різній основі (можна, навіть, на сукупності папірців, на яких записувати розраховані значення, або, навпаки, на одному великому листі паперу). Звісно, краще робити це на комп'ютері з використанням певного програмного забезпечення. Як ви розумієте, в цьому курсі ми використовуємо LO Calc.
Як ми це робили? Виділили на листі LO Calc зону для розміщення вхідних параметрів, зону розрахунків та зону виводу результатів. У зоні розрахунків крок за кроком приписали перший (нульовий, за нашою нумерацією) цикл. За результатами цього циклу почали наступний. Логічно розміщувати цикли в рядках, а певні показники, що розраховуються на кожному циклі — у стовпчиках. Нульовий рядок можна «розтягнути» на перший; відмінність між ними стосується лише того, як розраховується α-чисельність. Перший рядок, у такому разі, можна «розтягнути» на усі останні.
Засоби демонстрації вихідних результатів можуть брати те, що на рис. 4.12 названо інтегральними показниками, з самих розрахунків чи з особливого, окремого блоку (як це зроблено, наприклад, на рис. 4.10). За необхідності, крім динаміки можна вивести необхідний показник, що дозволить порівнювати різні прогони моделі (наприклад, чисельність популяції наприкінці 100-го циклу).
У вас не виникає відчуття дива? Ми розмістили на листі електронних таблиць певну кількість комірок, зв'язали їх нескладними формулами. Рутинна робота, але внаслідок її виконання модель «ожила». Можна змінювати початкові параметри та спостерігати, як буде змінюватися поведінка моделі. У певних випадках ці зміни будуть прогнозованими, інтуїтивно зрозумілими, в інших — навпаки, контрінтуїтивними. У будь-якому разі, виконання такої роботи на крок наближає до розуміння поведінки систем-оригіналів, до розуміння дійсності, яку повністю не може відбити ніяка модель.