| ← | → | |
| Приклад простої моделі: імітація експоненційного зростання | Ускладнення моделі: імітація логістичного зростання | Врахування демографічної структури: «Модель трьох поколінь» |
| Сотворіння світів-02 | Сотворіння світів-03 | Сотворіння світів-04 |
3. Ускладнення моделі: імітація логістичного зростання
3.1. Порівняння експоненційного та логістичного зростання
На попередньому етапі ми зробили модель, що описує експоненційне зростання популяції. Як ви пам'ятаєте з курсу екології, ускладненням експоненційної моделі є логістична (рис. 3.1). Бельгійський математик П'єр Ферхюльст (1804-1849) ввів в рівняння компонент, який забезпечує гальмування популяційного зростання в міру наближення до величини K — ємності середовища.
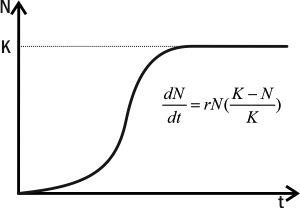
Рис. 3.1. Логістичне зростання (Шабанов, Кравченко, 2009)
Коли N мало, вираз в дужках практично дорівнює одиниці, і зростання мало відрізняється від експоненційного; коли N досягає величини K, приріст зупиняється, і чисельність популяції стає стабільною і відповідає K.
Внесемо в модель, створену на попередньому етапі, ще один стовпець, що відповідає логістичному зростанню. Щоб таблиця 3.1 відповідала моделі експоненційного зростання, створеній на попередньому етапі, ми додали в неї дві порожні перші рядки — в моделі вони зайняті інформаційним полем.
Таблиця 3.1. Додавання до моделі експоненційного зростання комірок, що імітують логістичне зростання
| A | B | C | D | |
| 1 | ||||
| 2 | ||||
| 3 | 0N= | 1000 | ||
| 4 | r= | 0,5 | ||
| 5 | К= | 10000 | ||
| 6 | t | N (exp) | N (log) | |
| 7 | 0 | 1000 {=B3} | 1000 {=B3} | |
| 8 | 1 | 1500 {=B7+B7*B$4} | 1450 {=C7+C7*B$4*(B$5-C7)/B$5} | |
| 9 | 2 | 2250 {=B8+B8*B$4} | ||
| 10 | 3 | 3375 {=B9+B9*B$4} |
Вводячи формулу в комірку C8 (саме її потім треба буде «розтягнути» на весь стовпець), врахуйте, що посилання на попередню комірку (C7) має бути відносним, а на комірки для введення параметрів (B2 і B3) — абсолютним, принаймні щодо рядка (B$2 і B$3 — цього достатньо, якщо формула буде «розтягуватися» всередині стовпчика).
Тепер можна заповнити формулами весь стовпець, що описує логістичне зростання, і вставити в файл графіки (рис. 3.2). Поєднувати на одному полі дві криві — експоненційного та логістичного зростання — не дуже зручно: розмірність шкали визначить експонента, що стрімко підіймається, і динаміка логістичного зростання буде непомітною. Може виявитися так, що для сприйняття зростання модельної популяції варто поєднати два способи представлення результатів: криві окремо (з діапазонами шкали, що відповідають значенням) і об'єднані на одному полі два графіки (зі штучно обрізаним діапазоном шкали).
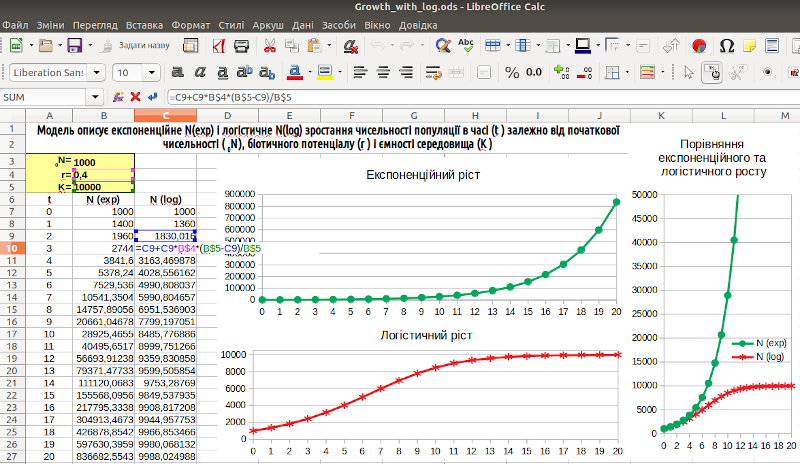
Рис. 3.2. Два способи порівняння експоненціального та логістичного зростання поруч; зверніть увагу: комірка C10 виділена, курсор на рядку формул, комірки, на які посилається формула, виділені кольоровими рамочками (при необхідності модель можна завантажити з сайту)
3.2. Врахування смертності в певному віці
Настав час задуматися, наскільки реалістична наша модель. Вона є імітаційним відображенням двох аналітичних моделей. На жаль, поки що при їх створенні ми не дуже-то замислювалися над тим, наскільки описувані такою моделлю процеси відображають дійсні події. Ця модель має кілька дуже серйозних відмінностей від біологічної дійсності, яку ми прагнули імітувати. Ми будемо наближатися до дійсності в кілька кроків, і їх порядок буде визначатися не стільки важливістю, скільки логікою засвоєння засобів моделювання.
У дійсному світі особини не тільки народжуються, але і гинуть (існує міф про «безсмертя» бактерій і найпростіших, але це, загалом, скоріше міф, ніж факт). Як його врахувати?
У експоненційної моделі облік смертності не настільки обґрунтований, як в логістичній. Експоненціальна модель побудована на твердженні dN/dt=r×N. Ми можемо окремо розглянути народжуваність і смертність і врахувати, що народжуваність збільшує чисельність популяції, а смертність — знижує. Ми можемо розглядати r як різницю між народжуваністю і смертністю.
У логістичної моделі ми приймаємо наявність народжуваності, яка залежить і від чисельності потенційних батьків, і від кількості доступного ресурсу. Насправді смертність теж повинна залежати від наявного ресурсу. Крім того, у різних видів ймовірність смерті протягом онтогенезу змінюється по-своєму, відображаючи особливості життєвого циклу (згадайте про криві смертності Р. Перля). Фактично, логістичну залежність можна отримати, прийнявши припущення про народжуваність, яка залежить тільки від чисельності потенційних батьків, і про смертність, яка залежить від доступного ресурсу. В цьому випадку ми розглянемо нескладний і досить умовний варіант.
Припустимо, потенційне зростання популяції відповідає логістичній моделі, але на кожному кроці в популяції гинуть особини, що народилося певний час назад (наприклад, три кроки назад). Крім того, приймемо, що на початковому етапі з'являються новонароджені особини, які будуть вмирати тільки на четвертому кроці (таблиця 3.2).
Таблиця 3.2. Порівняння логістичного зростання без урахування смертності особин та з її урахуванням
| A | B | C | D | |
| 1 | ||||
| 2 | ||||
| 3 | 0N= | 1000 | ||
| 4 | r= | 0,5 | ||
| 5 | К= | 10000 | ||
| 6 | t | N (логістичний) | N (логістичний зі смертю на 4-му кроці) | |
| 7 | 0 | 1000 {=B3} | 1000 {=B3} | |
| 8 | 1 | 1450 {=B7+B7*B$4*(B$5-B7)/B$5} | 1450 {=C7+C7*B$4*(B$5-C7)/B$5} | |
| 9 | 2 | 2069,9 {=B8+B8*B$4*(B$5-B8)/B$5} | 2069,9 {=C8+C8*B$4*(B$5-C8)/B$5} | |
| 10 | 3 | 2890,6 {=B9+B9*B$4*(B$5-B9)/B$5} | 1890,6 {=C9+C9*B$4*(B$5-C9)/B$5-C7} | |
| 11 | 4 | 3918,1 {=B10+B10*B$4*(B$5-B10)/B$5} | 2207,2 {=C10+C10*B$4*(B$5-C10)/B$5-C7*B$4*(B$5-C7)/B$5} |
У таблиці 3.2 розрахунки, що відповідають логістичному зростанню, перенесені в стовпець B (в LO Calc, як ви пам'ятаєте, досить виділити стовпець і перетягнути його). У стовпці C побудовано нову залежність.
В комірках 7-го рядка стоять ті ж самі формули та значення. Якби адресація в комірці B7 була абсолютною, формулу в ній можна було б просто «розтягнути» на комірку C7. А оскільки адресація в цій комірці відносна, формулу в ній можна скопіювати. Однак, зверніть увагу, що якщо ви просто скопіювали комірку B7 і вставите її в C7, LO Calc перепише формулу (вона буде вказувати на осередок C5). Діяти треба інакше: виділити комірку B7, увійти в рядок формул, виділити формулу, скопіювати її в буфер (Cntr+C), вийти з режиму редагування формули за допомогою клавіш Enter або Esc, увійти в комірку C7, перейти в рядок формул, вставити потрібну формулу (Cntr+V) і вийти за допомогою клавіші Enter.
Тепер побудуємо потрібну залежність. Формули в осередках C8 і C9 аналогічні таким в B8 і B9. Їх потрібно не копіювати, а розтягувати (посилання на вхідні дані в цих комірках мають абсолютний характер, а звернення до попередніх кроків мають адресуватися до комірок в стовпці C, а не B). В комірці C10 з'являється новація: потрібно врахувати загибель особин, що з'явилися в комірці C7. Починаючи з комірки C11, з формул треба віднімати приріст, який додавався три кроки назад. Так, з чисельності особин у комірці C11 треба відняти C7*B$4*(B$5-C7)/B$5, тобто приріст в комірці C8. Потім формулу, яка вийшла в комірці C11, можна «розтягнути» на весь стовпець.
Дослідіть отриману модель (рис. 3.3). Ви можете переконатися, що якщо r є досить великим (наприклад, r=0,5) чисельність стабілізується на рівні, нижчому, ніж K. Якщо r є невеликим (наприклад, r=0,3), чисельність популяції спочатку зростає, а потім, з появою смертності, знижується.
Чи є адекватною така поведінка моделі? Цілком. Як уже сказано, сама логістична модель будується на припущенні про смертність, залежною від доступності ресурсу. «Навісивши» на популяцію ще один потужний фактор, що призводить до зростання смертності, ми її з великою ймовірністю губимо.
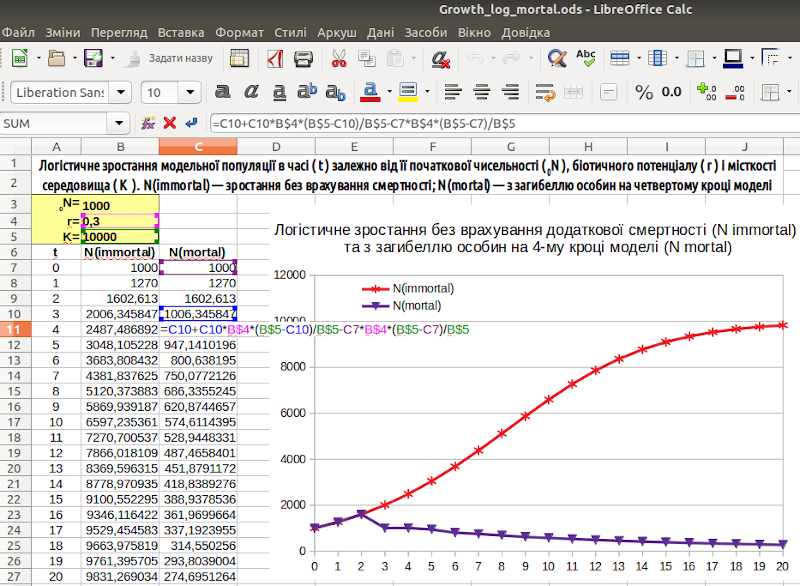
Рис. 3.3. Ми врахували смертність особин після досягнення ними певного віку. Показана формула в комірці С11; при необхідності, модель є доступною для завантаження
3.3. Чисельність популяції не може бути від'ємною
Використовуємо тільки що отриману модель ще для одного експерименту (не цілком коректного з біологічного погляду). Що буде, якщо r прийме від'ємне значення (наприклад, r =-0,1)? Біологічного сенсу тут небагато, оскільки від'ємне значення r може приймати в тому випадку, якщо в ньому вже враховується смертність, яку в даній моделі ми й так вже передбачили. Проте розглянемо і такий випадок. Результат показаний на рисунку 3.4.
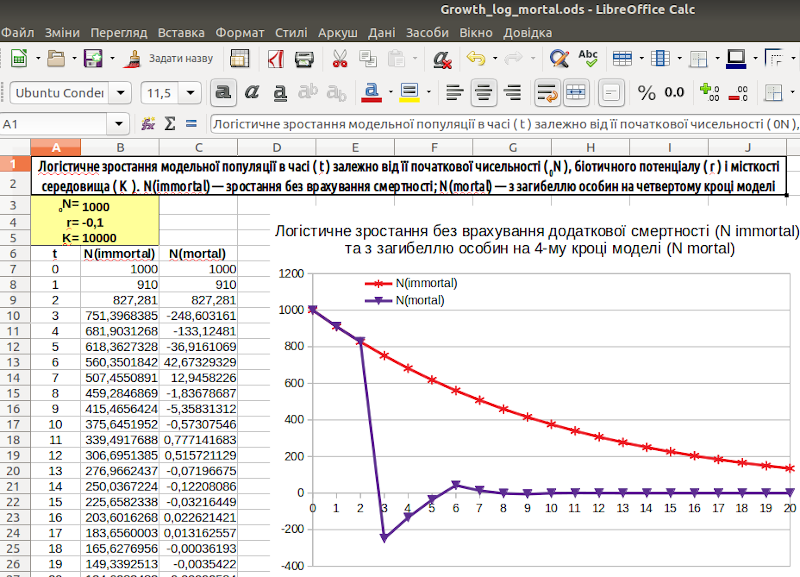
Рис. 3.4. Чи може чисельність популяції бути від'ємною?
Модель, що не передбачає смерть особин через 4 роки, поводиться адекватно: її чисельність крок за кроком знижується (і рано чи пізно дійде до нуля). А в моделі з загибеллю чотирирічних особин чисельність популяції на певному етапі (наприклад, на 3-му кроці в показаному на рис. 3.4 варіанті) стає від'ємною (а потім знову на якийсь час стає позитивною)! Має це будь-якої біологічний сенс? Ймовірно, не має (в якомусь випадку ми можемо вкласти в від'ємну чисельність якийсь сенс, але, ймовірно, це не той випадок). Ймовірно, потрібно зробити так, щоб чисельність популяції в нашій моделі не могла приймати від'ємні значення.
Таким чином, ми виявили умови, за яких модель поводиться неадекватно. Ймовірно, її слід перебудувати, щоб привести її у кращу відповідність до дійсності.
Для розв'язання цієї проблеми використовуємо одну з функцій LO Calc. Досі в формулах ми використовували дії. Крім того, ми можемо вводити в формули функції, вибираючи їх з досить великого набору. Функції мають назви, які набираються прописними буквами, а після назв в них завжди знаходяться круглі дужки, в яких можуть стояти необхідні дані. LO Calc і, наприклад, MO Excel мають сумісні набори функцій. Назви функцій можуть вводитися і показуватися на різних мовах. Наприклад, зараз ми обговорюємо функцію, яка англійською називається IF. Російський варіант цієї назви — ЕСЛИ. При переході з однієї мови на іншу електронні таблиці самі будуть переводити назви функцій. У цьому посібнику ми будемо використовувати англійські назви (наприклад, тому, що при написанні формул зручно не перемикати мови при необхідності використовувати символи, присутні тільки в англійській розкладці, як, наприклад, $). Для того, щоб вводити англійські назви функцій, треба включити їх в параметрах LO Calc. Пройдіть шляхом «Засоби / Параметри / LibreOffice Calc / Формули», і ви потрапите на діалог, показаний на рис. 3.5. Поставте «прапорець» на опції «Використовувати англійські назви функцій». До речі, на вкладці «Параметри мови» можна вибрати українську мову (на якій надаються наведені в цьому посібнику приклади), якщо в системі за замовчуванням встановлено якусь іншу мову.
Рис. 3.5. У цьому посібнику використовуються англійські назви функцій
Формат обговорюваної нами функції такий: IF(умова; результат_якщо_умова_виконується; результат_якщо_умова_не_виконується). У попередньому реченні після крапок з комами стоять пробіли (це необхідно для того, щоб запис формули адекватно відбивався у браузерах); в формулах Calc цих пробілів не має бути. Умовою може бути будь-який вираз, що використовує знаки =, >, <, > = (більше або дорівнює, не менше; ⩾; ≥), <= (менше або дорівнює, не більше; ⩽; ≤). Після першої точки з комою слід вказати, що функція вставить в комірку в разі якщо вираз є істинним, після другої — що повинно стояти в комірці, якщо вираз є хибним.
Так, в комірці C8 стояло {=C7+C7*B$4*(B$5-C7)/B$5}. Напишемо там {=IF((C7+C7*B$4*(B$5-C7)/B$5)<0;0;C7+C7*B$4*(B$5-C7)/B$5)}. Якщо результат обчислення для чисельності популяції виявиться від'ємним, ця функція підставить замість нього 0; в іншому випадку буде вставлений результат обчислень відповідно до початкової формули.
Забезпечимо подібним ускладненням всі рядки в розрахунках, — і результат обчислень ніколи не виявиться від'ємним. Щоб зробити це, треба вставити зазначену виправлену формулу в комірку C8 і «розтягнути» її на комірку C9, а потім змінити (подібним чином) вирази в комірках C10 і C11, і, нарешті, «розтягнути» комірку C11 до кінця стовпчика.
На жаль, на цьому складності не закінчуються. Кількість особин, яке вмирає на кроці, імітованому в комірці C11, розраховується як {C7*B$4*(B$5-C7)/B$5} — це приріст, який додався на кроці C8. Якщо величина r від'ємна, приріст в осередку C8 теж від'ємний. Віднімаючи від'ємну величину, ми отримуємо позитивну. Після того, як чисельність популяції знизилася до 0, вона продовжує рости! Природно, це не відповідає біологічної суті імітованих явищ. Як бути? Вставити ще одну функцію IF в уже наявну! Наприклад, це можна зробити так. Вставимо в комірку C11 вираз {=IF((C10+C10*B$4*(B$5-C10)/B$5-C7*B$4*(B$5-C7)/B$5)<0;0;IF(C7*B$4*(B$5-C7)/B$5>0;C10+C10*B$4*(B$5-C10)/B$5-C7*B$4*(B$5-C7)/B$5;C10+C10*B$4*(B$5-C10)/B$5))}. Його зміст такий: якщо чотири кроки назад чисельність модельної популяції збільшувалася, наявна чисельність скорочується на цю величину; якщо не збільшувалася — лишається без змін. Конструкція, яку ми використовували, мала такий вигляд:
IF(умова_1; результат_якщо_умова_1_виконується; якщо_умова_1_не_виконується_тоді_IF(умова_2; результат_якщо_умова_2_виконується; результат_якщо_умова_2_не_виконується)).
3.4. Округлення до цілих
Зверніть увагу, що в багатьох випадках результати обчислень представлені дробовими числами. Ця проблема складніша за попередню; річ у тому, що в ряді випадків дробові значення можуть мати сенс. Втім, для початку визначимо, як позбутися від нецілих значень.
По-перше, десяткові дроби можна просто не показувати. Це можна зробити, наприклад, за допомогою кнопки «Вилучити десяткове місце», яка разом з кнопкою «Додати десяткове місце» знаходиться на панелі інструментів за замовчуванням. Інший спосіб — можна натиснути правою клавішею миші на потрібній комірці, в контекстному меню вибрати «Формат комірок ...», а там — першу вкладку, «Числа». У віконці «Десяткові знаки» можна вказати кількість знаків після коми. У той же самий діалогове вікно можна потрапити в результаті виконання команд «Формат / Формат комірок...». На жаль, використання кнопки «Вилучити десяткове місце» часто призводить до помилки у показі результатів розрахунків; розглянемо таку ситуацію детальніше (рис. 3.6).
На рис. 3.6 «сходинками» показані послідовні етапи змін відображення певного результату обчислення. На першому кроці ми бачимо, як у комірці A1 відбивається результат обчислень за формулою {=1/3}. На наступному кроці можна впевнитися, що у контекстному меню «Формат комірок... / Числа» можна побачити, що цей результат є числовим, кількість десяткових знаків не зазначено, у комірці демонструється стільки цифр, скільки в неї вміститься, а в самому контекстному меню результат вказано з точністю до 15-го знаку. На третьому кроці користувач натиснув на кнопку «Вилучити десяткове місце», і в комірці опинилися символи ###, що свідчать про те, що результат обчислення не вміщується в наявні межі. Четвертий крок: «зменшення» кількості десяткових знаків призвело до того, що їх має вказуватися 14; звісно, такий результат не вміщується у комірку. П'ятий крок: кількість знаків зменшено до 3, і вони з запасом вміщуються у комірку.
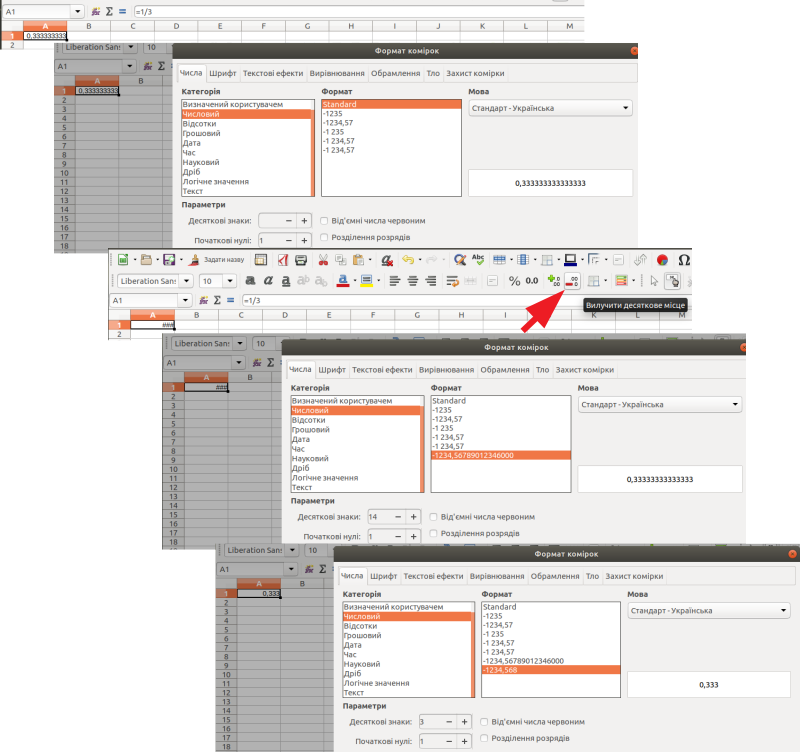
Рис. 3.6. Шість етапів перебудов показу результату обчислень у комірці A1; пояснення у тексті
В описаних випадках йдеться не про округлення чисел, а просто про те, скільки знаків буде демонструватися. Якщо LO Calc при цьому не буде показувати десяткові розряди, він все одно буде враховувати їх при обчисленнях: вони нікуди не дінуться, вони просто стануть невидимими.
Існує й інший шлях; нецілі значення можна округлити. Для цього можна використовувати команди ROUND(аргумент;кількість_розрядів), ROUNDUP(аргумент;кількість_розрядів) і ROUNDDAWN(аргумент;кількість_розрядів). ROUND(аргумент;кількість_розрядів) округлює відповідно до прийнятих правил округлення (значення, менші, ніж 0,5 округлюються в нижню сторону, а більші, ніж 0,5 — у верхню), ROUNDUP(аргумент;кількість_розрядів) округлює до верхнього значення, а ROUNDDAWN(аргумент;кількість_розрядів) — до нижчого. Роботу цих команд можна показати на прикладі, наведеному в таблиці 3.3. Числа, які стоять в заголовках рядків, в кожному стовпці тут округлені командою, що стоїть в заголовку стовпця.
Таблиця 3.3. Порівняння різних функцій LO Calc, що забезпечують округлення даних
| Число | ROUND(число;2) | ROUND(число;0) | ROUND(число;) | ROUNDUP(число;) | ROUNDDOWN(число;) |
| 1,345 | 1,35 | 1 | 1 | 2 | 1 |
| 1,5 | 1,50 | 2 | 2 | 2 | 1 |
| 1,666 | 1,67 | 2 | 2 | 2 | 1 |
Як ви можете побачити, якщо не вказувати кількість розрядів, аргумент буде заокруглений до цілих значень.
Отже, вказавши для всіх рядків нашої моделі округлення, ми отримаємо тільки цілі значення. Найкраще використовувати саме округлення за прийнятими правилами. Таке округлення надасть найменший вплив на кінцевий результат (округлення вниз буде його занижувати, а вгору — завищувати). Наведена в минулому підпункті формула для комірки C11 буде в такому випадку виглядати так:
C11 {=ROUND(IF((C10+C10*B$4*(B$5-C10)/B$5-C7*B$4*(B$5-C7)/B$5)<0;0;IF(C7*B$4*(B$5-C7)/B$5>0;C10+C10*B$4*(B$5-C10)/B$5-C7*B$4*(B$5-C7)/B$5;C10+C10*B$4*(B$5-C10)/B$5));)}.
3.5. Ймовірнісне округлення до цілих
Давайте тепер розглянемо ситуацію, коли дробові значення мають вагомий біологічний сенс. Наприклад, відомо, що проста відтворювальна народжуваність (кількість дітей на одну матір, при якому чисельність покоління дітей дорівнює чисельності покоління батьків) становить для високорозвинених країн 2,03, а для слаборозвинених — 2,2 (припустимо, що для України ця величина буде близька до 2,1). Якби у кожної матері (пари батьків) було рівно 2 нащадки (сумарний коефіцієнт народжуваності = 2), неминуча смертність привела б до того, що покоління дітей виявилося б менше, ніж покоління батьків. До речі, слід зазначити, що народжуваність в Україні набагато менша за відтворювальну...
А що означає сумарний коефіцієнт народжуваності 2,1? Матерів, які народжують одну десяту нащадка, на щастя, немає. Але така народжуваність буде характерна для випадку, коли в 9 сім'ях з 10 буде по 2 дитини, а в одній — 3 (21 дитина на 10 матерів). Округляючи таку величину за допомогою функцій ROUND і ROUNDDAWN, ми завжди отримаємо 2, а ROUNDUP — завжди отримаємо 3. А як зробити, щоб величина 2,1 округлялася до 2-х 9 разів з 10, а до 3-х - 1 раз з 10?
Для цього ми можемо скористатися функцією RAND(). Ця функція генерує випадкове число, що знаходиться між 0 і 1. До речі, функція RANDBETWEEN(нижча_межа;верхня_межа) задає діапазон, всередині якого має перебувати ціле випадкове число.
Для нас важливо те, що формула {= ROUNDDOWN(2,1+RAND();)} задає саме таку залежність, яка нам потрібна: в 9-ти випадках з 10-ти результат дорівнюватиме 2, а в 1-му — 3. При кожному перерахунку випадкове число буде приймати нове значення. У 9 випадках з 10 випадкова величина буде менше ніж 0,9, і значення суми округлятиметься до 2; в 1 випадку з 10 значення випадкової величини буде перебувати між 0,9 і 1, і значення суми округлятиметься до 3. Запустити такі перерахунки можна, натискаючи клавішу F9.
Таким чином, функція, яку ми редагували, повинна виглядати так (до речі, вона показана у вікні формул на рис. 3.7; можливо, там вона виглядає менш страхітливо):
C11 {=ROUNDDOWN(IF((C10+C10*B$4*(B$5-C10)/B$5-C7*B$4*(B$5-C7)/B$5)<0;0;IF(C7*B$4*(B$5-C7)/B$5>0;C10+C10*B$4*(B$5-C10)/B$5-C7*B$4*(B$5-C7)/B$5;C10+C10*B$4*(B$5-C10)/B$5))+RAND();)}.
Якщо вас лякає зовнішній вигляд цієї функції, не біда; він і повинен здаватися громіздким і незрозумілим для людини, яка раніше не працювала з подібними виразами. Сенс курсу моделювання, крім іншого, в тому, щоб навчитися вибудовувати такі вирази, розуміти їх і навіть знаходити в них, при потребі, помилки.
Два варіанти логістичної залежності, побудовані з випадковим округленням, наведені в цьому файлі. Завантажте (а краще — самі побудуйте!) його і дослідіть, як змінюється підсумковий результат при кожному натисканні клавіші F9 або виконанні команди «Дані / Обчислити / Переобчислити» (рис. 3.7).
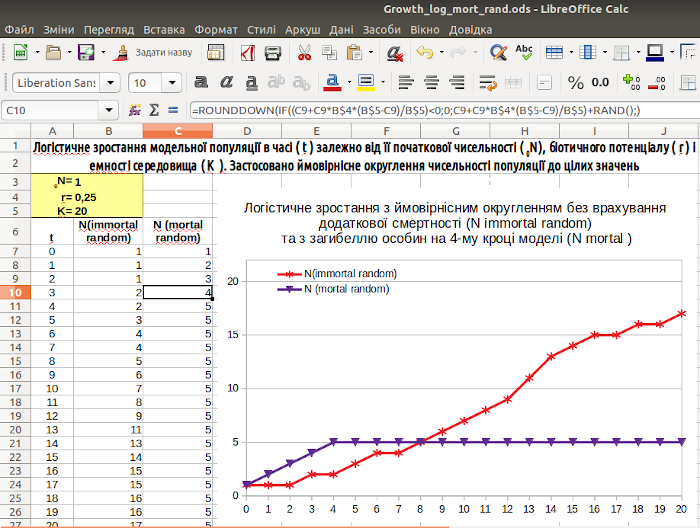
Рис. 3.7. Результат ймовірнісного округлення логістичного зростання з урахуванням і без урахування смертності. Зверніть увагу: на відміну від попередніх моделей результат цього моделювання є ймовірнісним; при натисканні на клавішу F9 результати зміняться. Наприклад, те, що на певних кроках зростання зі смертністю випереджує звичайне логістичне зростання, є випадковим
3.6. Приклад отриманого при моделюванні артефакту
У наведеному на рис. 3.7. прикладі встановлена дуже низька початкова чисельність популяції (1). Оскільки приріст при таких умовах невисокий, багато шансів, що він округлятиметься до нульового значення. Згодом ситуація змінюється, і чисельність починає рости. Чим вище чисельність популяції, тим менше (відносно) вплив на її зростання процедури округлення (розумієте, чому так виходить?).
Однак, наприклад, «популяція», чисельність якої протягом багатьох поколінь залишається рівною одиниці, в дійсності є неможливою. Випадковість впливає не тільки на кількість приплоду, а й на смертність дорослих особин. Стійкість модельної популяції з чисельністю в 1 особину є артефактом (тобто результатом дослідження, яке відображає не властивості досліджуваного процесу, а вплив використовуваної методики). Ви можете підібрати такі початкові параметри, що логістична модель призведе до необмеженого існування модельної популяції чисельністю в одну особину. Використовуваний нами алгоритм (відносно адекватний при одних умовах моделювання) привів до «виникнення» «популяції» з «безсмертної» особини.
Насправді в цьому випадку проявилася одна із загальних властивостей будь-яких моделей. Якщо модель задовільно відображає властивості системи-оригіналу в одних умовах, це не означає, що і в інших умовах модельні прогнози будуть відповідати дійсності. Вивчаючи простір станів моделі (сукупність значень вхідних параметрів) ми часто можемо побачити такі поєднання, при яких модель працює неадекватно. До речі, такий пошук часто допомагає зрозуміти щось нове не тільки про моделі, а й про систему-оригінал (це відбувається при з'ясуванні, чому ж оригінал відрізняється від моделі).
Що робити в такому випадку? Один варіант — використовувати наявну модель тільки в тій частині простору її можливих станів, де вона адекватна. Другий варіант — ускладнювати модель, наближаючи її до дійсності.