| ← | → | |
| Аналітичні вставки в імітаційній моделі | Підбір параметрів і пошук рішення | R як середовище для імітаційного моделювання |
| Сотворіння світів-06 | Сотворіння світів-07 | Сотворіння світів-08 |
7. Підбір параметрів і пошук рішення
7.1. Підбір параметра
Потужним інструментом електронних таблиць є засоби підбору параметрів. Пояснимо їх логіку спочатку на простому прикладі, а потім вже покажемо їх застосування для вирішення проблеми, де краще проявляється їх потенціал.
Штатний інструмент підбору параметра LO Calc ( «Засоби / Підбір параметра...») дозволяє вирішити таку задачу: визначити, при якому значенні однієї комірки (змінної) значення іншої комірки (цільової) дорівнюватиме певній величині. Природно, це можливо в тому випадку, якщо в цільовій комірці знаходиться формула, що залежить від значення змінної комірки.
Розглянемо такий приклад. Ми маємо ряд чисел, щодо яких ми знаємо (або прийняли рішення), який залежністю їх слід описувати, проте не знаємо значення параметра, що входить в цю залежність. Ми хочемо провести апроксимацію (пошук наближення, оптимального опису) цієї залежності. Використовуємо, наприклад, модель експоненційного зростання, найпершу модель нашого курсу (пункти 2.1 – 2.4). За допомогою нашої моделі створимо ряд чисел, що описують експоненційне зростання, а потім внесемо в отриманий результат стохастичні зміни (наприклад, у межах 10% від самого значення в обидва боки). Для цього достатньо помножити кожне значення на вираз (1-(0,5-RAND())/5); цей вираз продукує величину, що рівномірно розподілена між 0,9 до 1,1.
Можливо, ви не впевнені, що формула (1-(0,5-RAND())/5) дає розподіл між 0,9 до 1,1? Перевірити це можна за дві-три хвилини (якщо вміти користуватися електронними таблицями). Розглянемо цей приклад детальніше, оскільки він є гарним приводом познайомитися з новими засобами моделювання. Створимо службовий файл. Створимо в ньому 1000 комірок, в яких стоїть формула (1-(0,5-RAND())/5). Створимо ще 1000 комірок, де розрахуємо округлене значення цієї випадкової величини з точністю до двох десяткових знаків. Ви ж розумієте, що достатньо ввести ці формули у дві комірки, а потім «розтягнути» їх на 999 пар комірок, що лишилися? Щоб побачити такі формули, можна використати спосіб, який ми пояснювали під час розгляду біноміального розподілу в пункті 6.2. На лівій частині рис. 7.1. ввімкнуто перегляд формул (за допомогою команди «Перегляд / Показати формулу»), на правій – демонструються результати їх роботи.
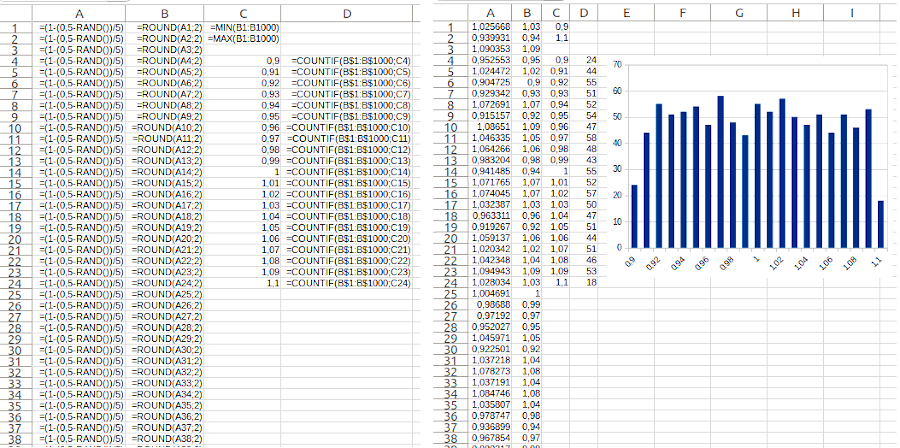
Рис. 7.1. Приклад перевірки розподілу, який продукує певна формула. На цьому рисунку поєднані два способи перегляду моделей; ліворуч – перегляд формул («Перегляд / Показати формулу»), праворуч – перегляд значень (та гістограма)
Перевіримо, які мінімальні та максимальні значення продукує формула, яку ми використовуємо, можна за допомогою функцій MIN(діапазон) та MAX(діапазон); використання таких формул є цілком інтуїтивно зрозумілим. Щоб оцінити характер розподілу, слід розрахувати чисельності окремих класів; використаємо для цього функцію COUNTIF. Побудуємо ряд чисел від мінімального до максимального значення з кроком, що відповідає кроку округлення; зрозуміло, що для цього достатньо ввести два перших значення та «розтягнути» його на потрібний діапазон. Поруч «розтягнемо» комірки з функцією підрахунку (звісно, з абсолютною адресацією там, де вона потрібна). Будуємо розподіл... і бачимо, що відхилення від рівномірності є, скоріше за все, випадковими. Ви зрозуміли, чому значення 0,9 та 1,1 мають зустрічатися, в середньому, у вдвічі меншій кількості випадків, ніж усі інші значення? До 0,9 округлюються лише значення «згори» (від 0,9 до 0,905), до 1,1 – лише «знизу» (від 1,095 до 1,1), а до усіх інших значень – як «згори», так і «знизу» (наприклад, до 1 – від 0,995 до 1,005).
Повернемося до головної задачі даного пункту: використанню формули, яку ми щойно перевірили, до випадкових змін членів ряду експоненційного зростання. На рис. 7.2 ви можете побачити, що це випадкова поправка може, наприклад, призводити до того, що наступний ряд цієї послідовності менше попереднього (зверніть увагу на 15-й і 16-й члени ряду, на 21-му та 22-му рядках).
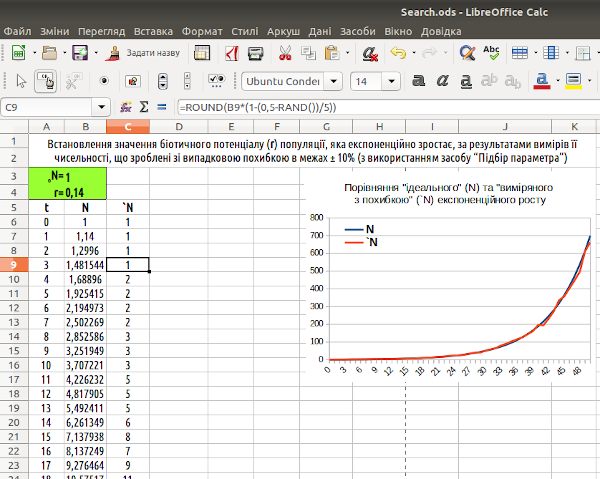
Рис. 7.2. У стовпці C – значення зі стовпця B, змінені множенням на випадкову величину в межах ± 10% (зверніть увагу на рядок для формул)
Припустимо, що за значеннями в стовпці C нам треба встановити параметри, за якими побудована послідовність в стовпці B (а самі значення в стовпці C можна розглядати, як вимірювання значень в стовпці B з певною похибкою). Нам треба побудувати ще одну послідовність, яку ми будемо будувати відповідно до обраної нами закономірності та «підганяти» (змінювати таким чином, щоб максимально наблизити) цю закономірність під значення в стовпці C. Ми зробимо це в стовпці E. Заповнимо стовпчик E такою ж послідовністю, як і стовпець B, тільки замість невідомого нам (по стовпцю C) значення r введемо (в клітинку E3) значення ~r – наближення до r. Ми можемо поставити ~r яким завгодно – наприклад, рівним 1, як це зроблено на рис. 7.3. Тепер ми можемо порівняти наявні у нас значення в стовпці з C наближеннями до них в стовпці E. Для цього порівняння в стовпці F у кожному рядку розрахуємо квадрат різниці між відповідними значеннями з C і E. У комірці E4 розрахуємо суму всіх таких квадратів різниці між значеннями з двох рядів. На рис. 7.3 показані формули, завдяки яким це зроблено.
Можна сказати, що у стовпці E знаходиться модель оригінала, що перебуває у стовпці C; стовпець C є штучно спотвореною моделлю ряду, що перебуває у стовпці A. Таким чином, у стовпці E перебуває непряма модель послідовності зі стовпця A.
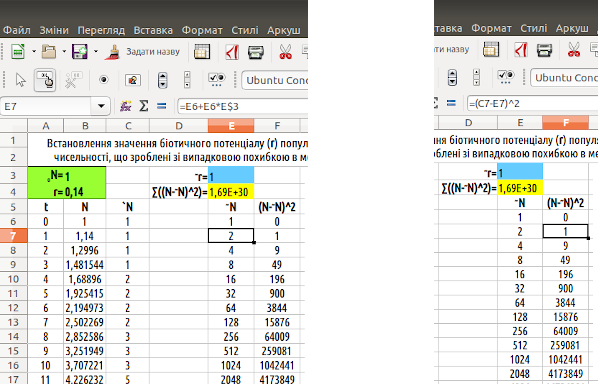
Рис. 7.3. Побудова послідовності, що завдяки процедурі оптимізації має наблизитися до експоненційної послідовності, параметр r в якій є «невідомим» для інших стовпчиків моделі, ніж стовпчик B. Праворуч показано приклад формули, що розраховує експоненційну послідовність на підставі значення ~r; праворуч – приклад формули, що розраховує квадрат різниці між «вимірами з похибкою» та нашим наближенням
Зверніть увагу на важливу обставину. Ми будуємо наближення до ряду «вимірів з похибкою», яке підкоряється експоненційному закону. Завдяки цьому ми плануємо узнати параметр r, за яким побудовано «невідому» нам справжню експоненційну послідовність. Ми сподіваємося, що, оскільки членів цієї послідовності досить багато (на рис. 7.2 можна побачити, що ми розглядаємо перші 50 значень ряду експоненційної послідовності), похибки врівноважать одна одну, і ми досить точно узнаємо «справжнє» значення r. Чи важливо для нас, з якого значення ~r ми почнемо наші пошуки? Ні! Важливо не те значення, з якого ми почнемо, а те, як ми будемо наближатися до тієї величини, яку ми шукаємо. До речі, у складних задачах оптимізації з багатьма параметрами на результат пошуку впливає, з якого початкового значення ми будемо починати, але в цьому прикладі ми можемо почати з будь-якого значення (перевірте самі!). Як визначити, наскільки добре ми отримали наближення? Розрахувати міру невідповідності моделі та оригіналу (у нашому випадку – експоненційного зростання, що розраховане на підставі ~r та ряду «вимірів з похибкою»). Розрахуємо цю міру у комірці E4 (на рис. 7.4 можна побачити, що у разі значення ~r, узятого ряду «зі стелі» значення міри невідповідності буде дуже великим). На рис. 7.4 ця міра невідповідності позначена формулою, але ми можемо застосувати до неї позначення G (від англ. gap – розрив). Крім того, на рис. 7.4 показано, як викликати функцію «Засоби / Підбір параметра...».
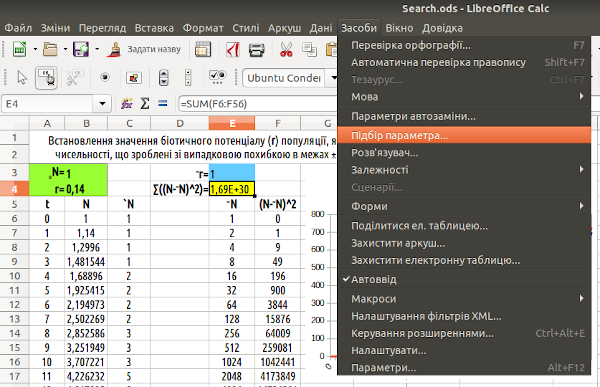
Рис. 7.4. У комірці E4 розраховується G – міра невідповідності моделі та оригінала; показано, як викликати діалог «Підбір параметра...»
З'явиться діалог, в якому ми повинні будемо вказати цільову комірку з функцією, що залежить від комірки зі змінюваним значенням. Зазначимо, що ми хочемо отримати в цільовій комірці значення 0 (це, звісно, неможливо, оскільки відповідає випадку ідентичності значень у двох стовпцях; в усякому разі, LO Calc буде намагатися наблизитися до цього значення). Змінна комірка – осередок зі значенням ~r (рис. 7.5).
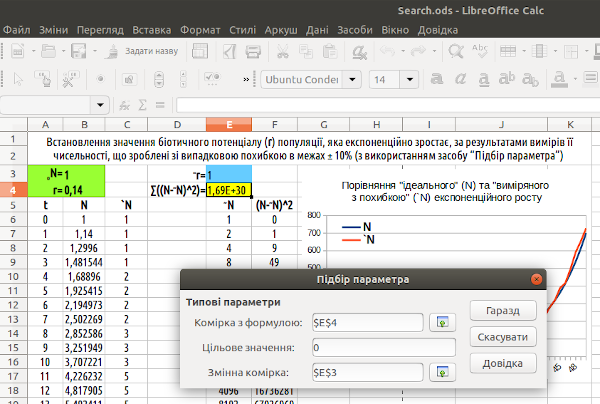
Рис. 7.5. LO Calc буде мінімізувати (наближати до 0) значення у комірці E4, змінюючи значення в комірці E3
Природно, значення в цільовій комірці не може досягти 0. LO Calc знаходить найкраще наближення і повідомляє про це (рис. 7.6).

Рис. 7.6. LO Calc запропонував прийняти найкраще наближення, яке він знайшов
Після того, що знайдене наближення буде прийнято, програма підставить його в комірку для ~r. Треба зазначити, що наближення виявилося зовсім непоганим (рис. 7.7).
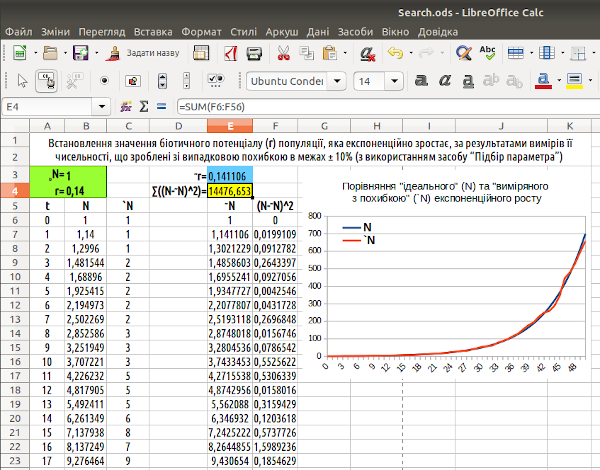
Рис. 7.7. Результат підбору параметра. Наближення (0,1411) відрізняється від значення, яке треба було встановити (0,14), але відповідність цілком непогана
Чи можна покращити цей результат? Без сумнівів. Один із шляхів є таким. Як міру G (невідповідності між моделлю та оригіналом) ми застосовували суму квадратів відхилень: G1=∑((N-~N)2). Втім, можливі й інші рішення. Ряд, з яким ми працюємо, зростає прискорено. Перший член ряду – 1, п'ятдесятий – 700; розходження на 1% відносно першого члену ряду відповідає 0,01, а відносно п'ятдесятого – 7. Як зробити так, щоб зменшити вплив «масштабу»? Перевірте самостійно, наскільки зміниться точність оцінки r, якщо мінімізувати величину G2=∑((N-~N)2/(N+~N))!
7.2. Пошук рішення з кількома параметрами
LO Calc має й інструмент для пошуку оптимального розв'язання задач з кількома змінними. Це «Розв'язувач...», посилання на який можна побачити на рис. 7.4 під посиланням на «Підбір параметра...» у меню «Засоби». На жаль, цей інструмент LO Calc є слабшим, ніж аналогічний інструмент в MO Excel, оскільки працює лише з лінійними рівняннями (тобто, може бути використаним лише в відносно простих випадках). Втім, насправді LO Calc є більш потужною програмою, оскільки для нього існує розширення NLPSolver, що є придатним для нелінійних задач.
Щоб розглянути роботу засобів для пошуку рішення з кількома змінними, використовуємо дані про вік і довжину тіла 100 самиць озерних жаб, Pelophylax ridibundus, що узяті з дисертаційної роботи О. Є. Усової (2016).
Таблиця 7.1. Вік (в роках) і довжина тіла (в 0,1 мм) 100 самиць озерних жаб, Pelophylax ridibundus (Усова, 2016)
|
Вік |
Довжина |
Вік |
Довжина |
Вік |
Довжина |
Вік |
Довжина |
Вік |
Довжина |
|
4 |
245 |
3 |
347 |
5 |
462 |
7 |
644 |
6 |
859 |
|
3 |
263 |
5 |
349 |
3 |
464 |
5 |
650 |
7 |
861 |
|
3 |
291 |
3 |
358 |
4 |
486 |
7 |
672 |
5 |
865 |
|
3 |
304 |
4 |
358 |
5 |
502 |
4 |
685 |
9 |
867 |
|
3 |
305 |
3 |
359 |
4 |
522 |
5 |
689 |
7 |
868 |
|
4 |
306 |
4 |
373 |
7 |
524 |
6 |
702 |
6 |
871 |
|
4 |
310 |
5 |
376 |
5 |
549 |
5 |
715 |
6 |
878 |
|
3 |
312 |
3 |
378 |
6 |
549 |
9 |
722 |
7 |
883 |
|
3 |
313 |
4 |
379 |
3 |
557 |
5 |
729 |
7 |
895 |
|
3 |
319 |
3 |
383 |
6 |
560 |
6 |
743 |
7 |
901 |
|
5 |
320 |
5 |
384 |
6 |
566 |
7 |
755 |
7 |
903 |
|
3 |
322 |
5 |
395 |
7 |
568 |
7 |
759 |
10 |
931 |
|
3 |
324 |
3 |
396 |
6 |
591 |
8 |
785 |
8 |
934 |
|
3 |
326 |
4 |
408 |
4 |
595 |
8 |
790 |
10 |
959 |
|
4 |
326 |
3 |
410 |
6 |
596 |
5 |
792 |
8 |
979 |
|
4 |
335 |
4 |
420 |
7 |
607 |
5 |
801 |
7 |
990 |
|
4 |
339 |
5 |
424 |
7 |
619 |
7 |
805 |
6 |
1026 |
|
4 |
342 |
5 |
425 |
6 |
620 |
8 |
822 |
7 |
1042 |
|
5 |
344 |
6 |
434 |
6 |
634 |
8 |
828 |
7 |
1055 |
|
5 |
345 |
5 |
447 |
6 |
642 |
6 |
852 |
8 |
1211 |
Наша задача – встановити, за якою закономірністю відбувається збільшення розміру цих жаб з віком. Інакше кажучи, знайдемо рівняння регресії (від лат. regressio – «зворотний рух», тобто перехід не від рівняння до значень, а навпаки – від значень до рівнянь). Використаємо для цього моделювання. Позначимо вік особин літерою A, а довжину – L. Врахуйте, що в моделях, що описують зростання особин, деякі позначення можуть мати інший сенс, ніж в моделях, що описують популяційну динаміку (букв в абетці не вистачає!).
Найпростішою математичною моделлю, що може бути застосована для опису зростання особини, є пряма лінія: y = a + b*x. Коефіцієнт b визначає кут, під яким проходить ця пряма (наприклад, якщо b=1, ця пряма проходить під кутом 45˚ проти годинникової стрілки відносно вісі абсцис). Коефіцієнт a визначає зсув догори або униз цієї прямої відносно початку координат (якщо a=1, ця пряма проходить через початок координат). Змоделюємо зростання жаб, дані про яких наведені в таблиці 7.1, за допомогою такого рівняння.
Підхід, що ми використаємо, буде аналогічним такому у попередньому випадку. У нас є дані про A та L, що залежить від A. Це – емпіричні дані, вони не залежать від нас. Ми змоделюємо L за допомогою величини ~L (L з тильдою), яка буде залежати від коефіцієнтів a і b: ~L = a + b*A. Для цього треба задати певні значення коефіцієнтів a і b та розрахувати для кожної особини, залежно від її віку, очікувану згідно з моделлю довжину тіла ~L. Модель буде гарною, якщо для усіх жаб емпіричне L та розраховане ~L будуть добре відповідати одне одному. Щоб забезпечити таку відповідність, нам треба буде визначити міру відмінностей між моделлю та емпіричними даними G, а потім мінімізувати G, змінюючи a і b. Як це зробити, показано на рис. 7.8.
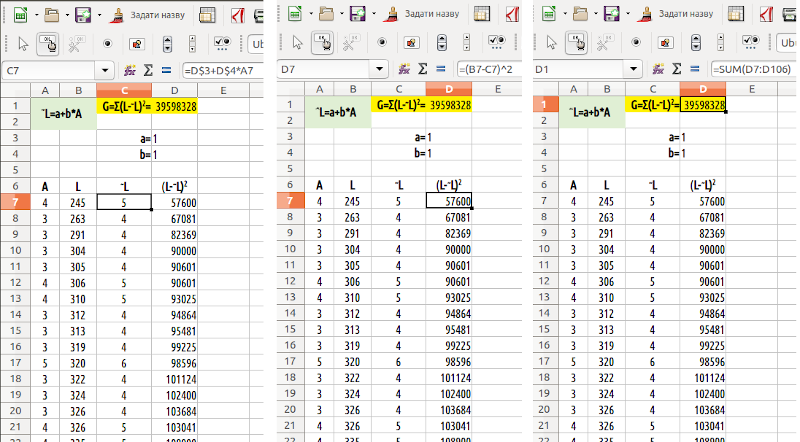
Рис. 7.8. Показано формули, що потрібні для розрахунку ~L та G
Щоб мінімізувати G, змінюючи a і b, необхідно інсталювати додаток NLPSolver. Те, як це робити, залежить від операційної с системи та іншого програмного забезпечення, яке встановлено на комп'ютері, яким ви користуєтеся. Наприклад, на Ubuntu, яким користується автор цього курсу, достатньо виконати такі команди:
sudo apt update
sudo apt install libreoffice-nlpsolver
На Windows-комп'ютерах розв'язання цієї задачі може бути складнішим (дякую Катерині Нестеренко, яка в цьому розбиралася!). Для встановлення NLPSolver на такий комп'ютер необхідно завантажити інсталяційний файл та запустити його, погодившись зі всіма пропозиціями під час інсталювання. У разі виникнення помилки "Could not create Java implementetion loader", або повідомлення про необхідність jre-середовища, слід завантажити інсталятор Java звідси, встановити його на комп'ютер, а після цього вже інсталювати NLPSolver.
Будемо виходити з того, що ви впоралися з установкою NLPSolver. Викликайте «Розв'язувач» (як це зробити, видно на рис. 7.4), задайте умови оптимізації (рис. 7.9). Врахуйте, що розв'язати цю задачу ви зможете лише з встановленим NLPSolver.
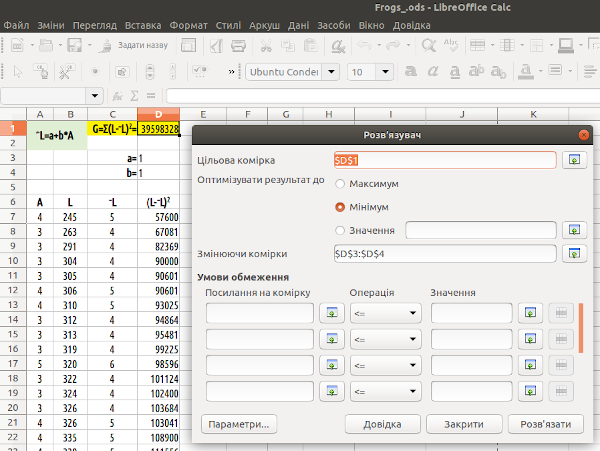
Рис. 7.9. Задані цільові та змінні комірки
Щоб обрати алгоритм, зайдіть у меню «Параметри». В діалозі «Механізм розв'язувача» ви можете обрати один з чотирьох алгоритмів (рис. 7.10).
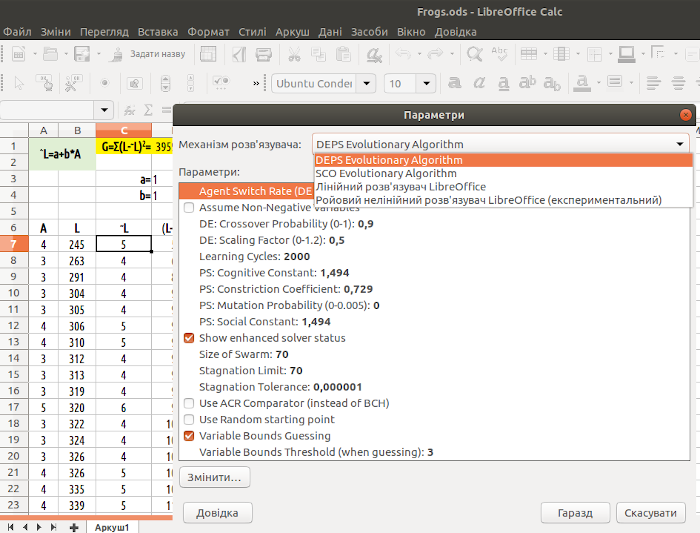
Рис. 7.10. Якщо ви встановили NLPSolver, ви можете обирати один з чотирьох алгоритмів
Порівняємо ці алгоритми. Запропонуємо початкові значення: a=1; b=1. Як при використанні «DEPS Evolutionary Algorithm», так і при використанні «SCO Evolutionary Algorithm» з параметрами за замовченнями перший запуск розв'язувача дає a=4; b=4. Це є наслідком того, що ці алгоритми шукають рішення на віддаленні від початкового значення, що не перевершує певний ліміт. Обидва параметри можуть змінюватися не більш ніж в 4 рази. Другий запуск закінчується на значеннях a=16; b=16, третій – a=64; b=64, а ось четвертий – a=21,911; b=105,836. Останнє значення не змінюється при наступних запусках розв'язувача. Спроба обрати «Лінійний розв'язувач LibreOffice» нічим хорошим не закінчується: програма повідомлює, що даний випадок є нелінійним. Якщо обрати «Ройовий нелінійний розв'язувач LibreOffice (експериментальний)», розв'язувач на певний час завмирає, а потім відразу знаходить рішення a=21,911; b=105,836.
Щоб зрозуміти, що ми отримали, додамо діаграму. Виділимо дані у стовпчиках A, B і C. Пройдемо шляхом «Вставка / Діаграма... / Діаграма XY / Лінії та точки». Оберемо опції «Рядки даних у стовпцях» та «Перший стовпчик як підпис». Додамо необхідні підписи. Ми отримаємо щось на кшталт діаграми, показаної на рис. 7.11.
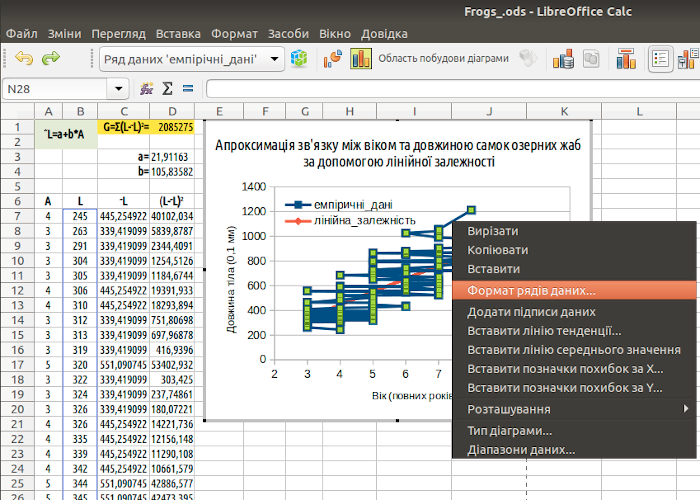
Рис. 7.11. Щоб зробити цю діаграму зрозумілою, слід для емпіричних даних залишити тільки піктограми, а для розрахованої залежності – тільки лінію
Після певної перебудови (увійти у графік, клікнути правою клавішею миші на лінії, обрати «Формат рядів даних...» та відредагувати, як слід, можна отримати таку діаграму, як на рис. 7.12.
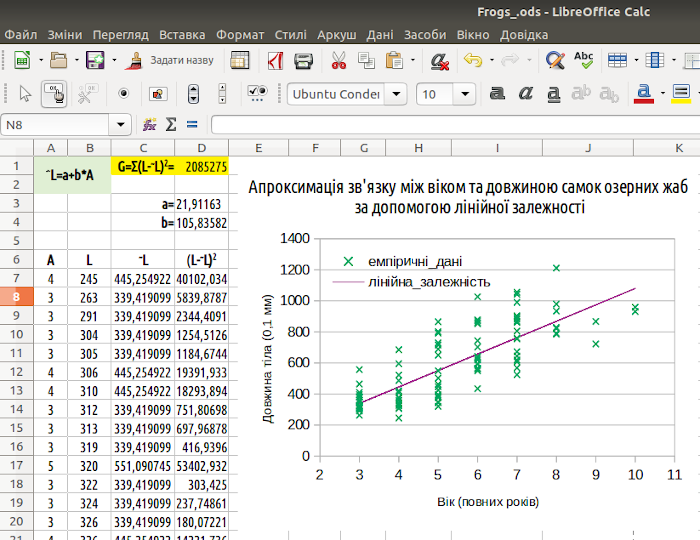
Рис. 7.12. Щоб зробити цю діаграму зрозумілою, слід для емпіричних даних залишити тільки піктограми, а для розрахованої залежності – тільки лінію
Ми підібрали (методом найменших квадратів, тобто шляхом мінімізації розбіжностей між емпіричними даними та моделлю) лінійну залежність (лінію регресії), що описує зростання розмірів самиць озерних жаб зі збільшенням їх віку. Здається, в отриманого розподілу є одна цікава особливість: жаби старших вікових груп менші, ніж можна було чекати за отриманою залежністю, а жаби середніх вікових груп – або більші, або менші. Як в цьому впевнитися?
7.3. Приклад аналізу результатів за допомогою умовного форматування
Побудуємо розподіл жаб кожної вікової групи відносно того розміру, який ми вважаємо для цієї групи характерним (згідно з моделлю, отриманою на рис. 7.11). У стовпчику B у нас містяться справжні розміри жаб, у стовпчику C – очікувані згідно з нашою моделлю (~L=21,9+105,8*A). Розрахуємо у стовпчику E відносний розмір жаби (у порівнянні з очікуваним). У стовпчику F визначимо, до якої з розмірних груп належить кожна жаба. Для цього розділимо шкалу відносного розміру на 6 рівних діапазонів між мінімальним та максимальним відносним розміром. Округлимо відносний розмір кожної жаби до одного з цих класів. Це дасть 7 розмірних класів (менше першого; перший; другий, третій, четвертий, п'ятий та шостий). Клас «менше першого» буде представлений нулем; щоб усі номері класів відповідали натуральним числам, додамо до їх номерів одиницю. Ми отримаємо 7 розмірних класів, як показано на рис. 7.13. До речі, ви розумієте причини, за якими 1-му і 7-му класу відповідають вдвічі вужчі діапазони, ніж іншим? Це ті самі причини, за якими вдвічі меншими були першій і останній класи розподілу, який ми розглядали на рис. 7.1.
При побудові розподілів для кожного віку (на нижньому скрині на рис. 7.13 вони знаходяться у стовпчиках I – P) слід вказувати ті діапазони рядків, що відповідають особинам певного віку.
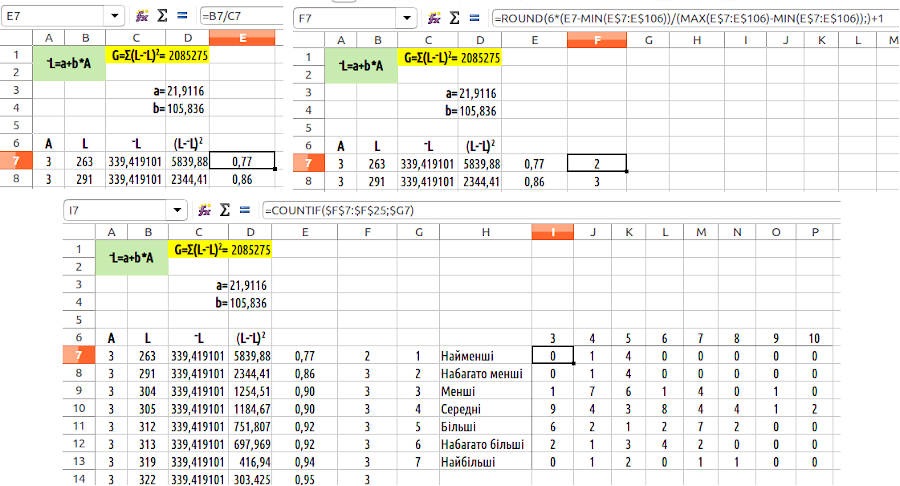
Рис. 7.13. На трьох фрагментах скринів можна побачити формули, за якими побудовано розподіли. Розберіться, як працюють ці формули!
Ви зрозуміли, чому відрізок між мінімальним та максимальним відносним розміром треба було розділити на 6 відрізків (або на іншу парну кількість)?. Розділ на парну кількість відрізків призведе (при звичайному округленні) до появи непарної, на одиницю більшої кількості класів. Середній клас (у нашому випадку, після застосування поправки на 1, це 4) відповідає особинам, розміри яких приблизно такі, як прогнозує модель.
Як покращити візуалізацію розподілу у таблиці, яку ми побудували у стовпчиках I – P? За допомогою умовного форматування. Щоб викликати його варіант, який пропонований на рис. 7.14, слід пройти шляхом «Формат / Умовне форматування... / Колірна шкала...».
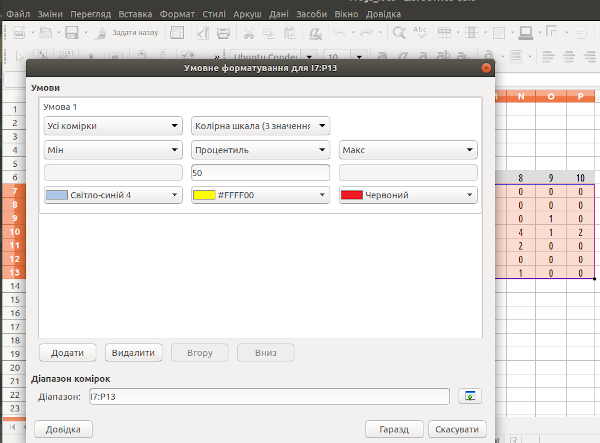
Рис. 7.14. Діалог настройки колірної шкали
Щоб підкреслити 4 розмірний клас, що відповідає середнім за розмірам особинам. Візьмемо його у рамку «Формат / Комірки... / Обрамлення» або після кліку правою клавішею миші «Формат комірок / Обрамлення». Кінець кінцем, ми отримуємо результат, показаний на рис. 7.15.
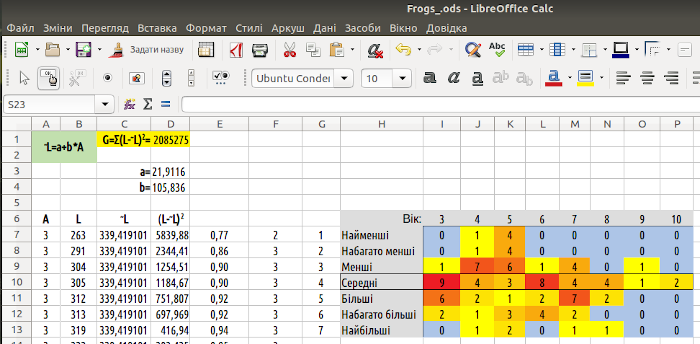
Рис. 7.15. Порівняйте цей спосіб візуалізації даних з тим, що показано на рис. 7.12! Ці два способи є взаємодоповнювальними...
В усякому разі слід зазначити, що розподіл особин за віком та розміром, що був отриманий емпірично, не дуже переконливо описаний за допомогою одного рівняння лінійної регресії...
7.4. Дві лінійні залежності для двох внутрішньопопуляційних стратегій
Може, якщо однієї прямої недостатньо, можна спробувати дві? Це не єдиний шлях покращення застосованої нами моделі; наприклад, можна спробувати ускладнити залежність, яка апроксимує наявний розподіл. Втім, автор цього курсу робив такі спроби на подібному матеріалі та не був задоволений результатом. Ми розглянемо варіант, що відповідає концепції внутрішньопопуляційних онтогенетичних стратегій, яка викладена в цих двох статтях:
Шабанов Д. А., Коршунов А. В., Кравченко М. А., Мелешко Е. В., Шабанова А. В., Усова Е. Е. Внутрипопуляционные онтогенетические стратегии скороспелости и тугорослости: определение на примере бесхвостых амфибий // Вестник Харьковского национального университета имени В.Н.Каразина, серия "Биология". — 2014. — Вып. 22. — с. 115-124.
Усова Е.Е., Кравченко М.А., Шабанов Д.А. Внутрипопуляционные онтогенетические стратегии у зеленых лягушек (Pelophylax esculentus complex) // Вісник Харківського національного університету імені В.Н.Каразіна, серія "Біологія". — 2015. — Вип. 25. — С. 223-238.
Задамо (поруч з попереднім блоком даних, щоб легше було порівнювати) дві модельні залежності, для ~SL та ~BL (від S — small, B — big). Розрахуємо відстань від кожної точки до найближчої прямої (формулу можна побачити на рис. 7.16). Ми впевнилися, що рішення, яке пропонує NLPSolver, залежить від початкової точки. Отже, задамо початкові значення для двох прямих так, щоб вони були наближені до попереднього рішення, але одна з них йшла нижче, а друга — вище.
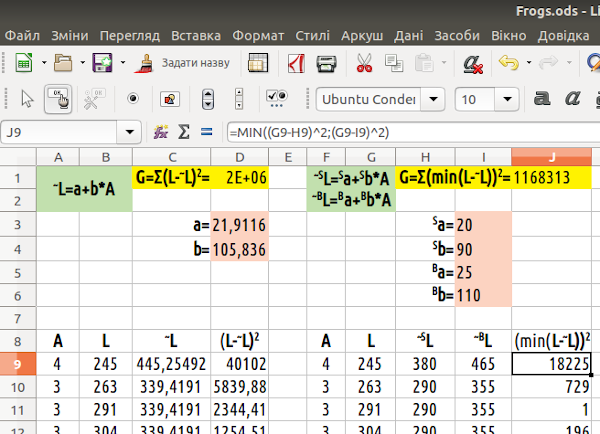
Рис. 7.16. Модель для двох прямих, ~SL=Sa+Sb*A та ~BL=Ba+Bb*A
Запустимо «Розв'язувач»; задамо цільову та змінні комірки; оберемо «DEPS Evolutionary Algorithm» або «SCO Evolutionary Algorithm» (рис. 7.17). Можна спробувати працювати й з опцією «Ройовий нелінійний розв'язувач LibreOffice (експериментальний)», але в автора цього посібника ройовий розв'язувач при застосуванні в описуваній задачі видавав неадекватні рішення (збільшував, а не зменшував значення цільової комірки).
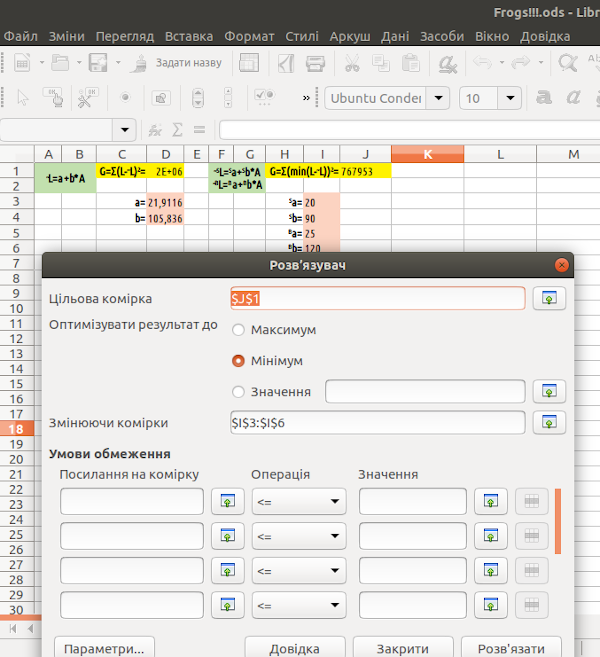
Рис. 7.17. Умови задані...
Запустимо «Розв'язувач»; алгоритм покаже, як він шукає рішення (рис. 7.18).
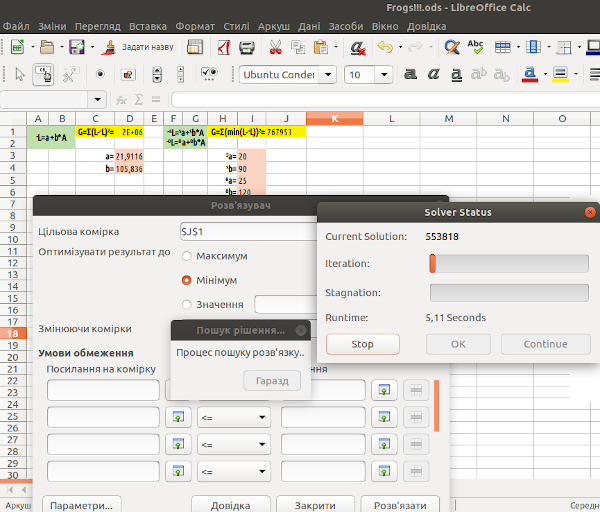
Рис. 7.18. «DEPS Evolutionary Algorithm» демонструє, як він шукає рішення
Перший пошук, який зробив автор, дав «підозріле» рішення: Sb=100. Ми вже знаємо, що «DEPS Evolutionary Algorithm» та «SCO Evolutionary Algorithm» змінюють початкові значення не більше, ніж в 4 рази; запустимо пошук повторно. Остаточне рішення показане на рис. 7.19, там також додано графік, що дозволяє візуалізувати таке рішення.
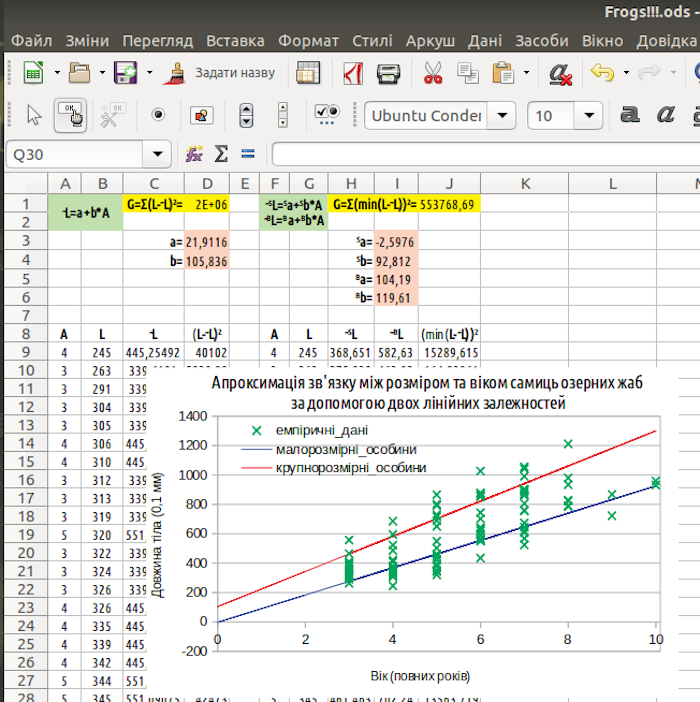
Рис. 7.19. Це рішення виявилося оптимальним після низки запусків алгоритмів оптимізації з різними початковими значеннями
Графік, показаний на рис. 7.19, має одну суттєву відмінність від аналогічного графіку на рис. 7.12: прямі, що відповідають отриманим лініям регресії, продовжені до нульового віку. Для цього у діапазон даних, за якими будується графік, додані ще три рядки, що не відповідають емпіричним даним (рис. 7.10).
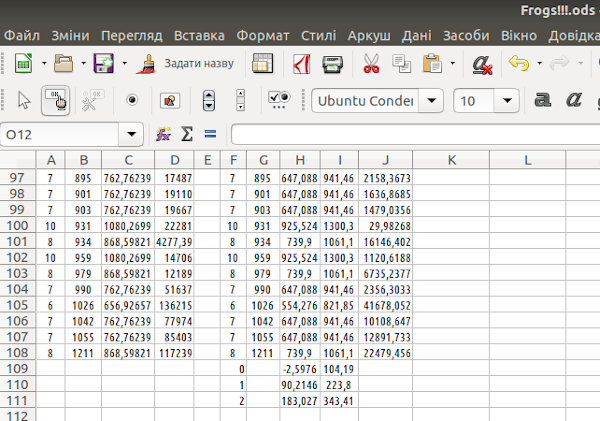
Рис. 7.20. Рядки 109—111 містять точки, які дозволяють добудувати модельні криві для віків жаб, що не були представлені у досліджуваній вибірці
Таким чином, модель з двома лініями регресії побудована. Вона, безумовно, краще описує різноманіття емпіричних даних, ніж модель з однією лінією. Втім, можливо, наявні дані можна описати ще краще. Як – питання лишається відкритим...