4 Перше знайомство з використанням R
Щоб почати роботу з R, його слід або встановити на свій комп’ютер, або скористуватися онлайн-сервісом (наприклад, таким). На погляд авторів курсу, перший шлях є кращим, але (щоб далі до цього не вертатися) скажемо кілька слів про інший, не рекомендований нами шлях.
Рис. 4.4.1 Сервіс Posit cloud пропонує хмарний доступ до R та RStudio. Ви можете зареєструватися тут та обрати вільний доступ (що має суттєві обмеження). На жаль, таке рішення є незручним
Набагато краще рішення — інсталювати R та RStudio на своєму комп’ютері. Для цього слід завантажити інсталятори цих програм та по черзі запустити їх на локальному комп’ютері. Зверніть увагу: встановлювати RStudio слід обов’язково після R, а не до нього. Спочатку ви інсталюєте R, потім — RStudio, а далі ви будете запускати саме RStudio і працювати в ньому; ця оболонка сама звернеться до своєї основи.
Інсталятор R (для вашої операційної системи) ви маєте завантажити тут.
Інсталятор RStudio (для вашої операційної системи) ви маєте завантажити тут. RStudio розраховано на 64-бітні операційні системи, але у разі, якщо у вас — стара 32-бітна система, ви можете використати відповідний варіант з-поміж старих версій.
Після того, як інсталяція відбулася, викликайте RStudio і починайте працювати!
Ви викликали RStudio. Що ви бачите?
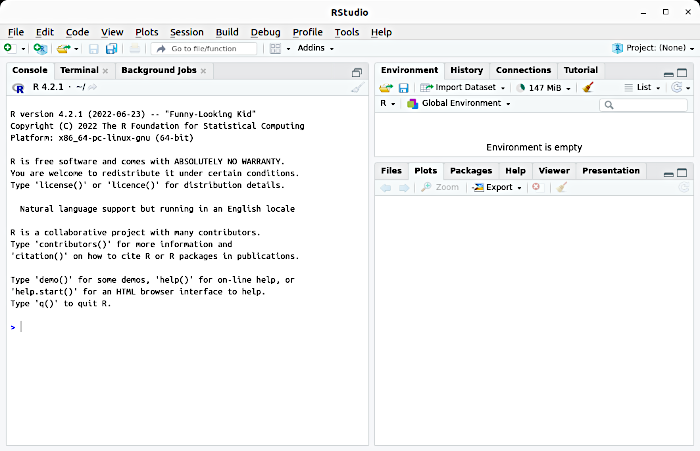
Рис. 4.1.2 Вікно RStudio. У правій частині екрана — автоматично згенеровані вступні пояснення
Ліва частина екрана RStudio зайнята консоллю — «пристроєм» для вводу та виводу інформації. Після знаку > стоїть курсор. Наберіть там 2*2 і натисніть Enter. Ви бачите, що можете використовувати R через консоль, і це стосується не лише використання у якості калькулятора.
Втім, команди ми будемо давати переважно не в консолі, а у редакторі скриптів — вікні, що призначене для створення в ньому послідовності команд. У такому стані, як на рис. 4.1.1, редактор скриптів ще не відкритий. Викличте меню RStudio і запропонуйте створення нового файлу. Ви побачите додаткове меню, де треба буде обрати тип такого файлу.
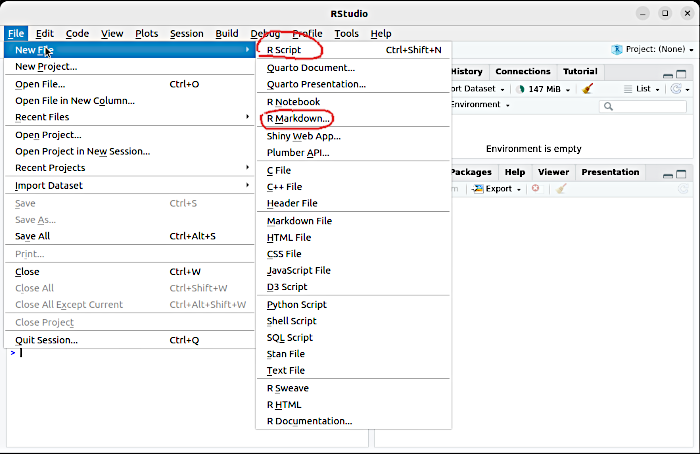
Рис. 4.1.3 Так відкриваються нові вікна для скриптів та документів RMarkdown. Ми почнемо нашу роботу зі скриптів
Ми будемо працювати з двома типами файлів. Перш за все, це — скрипти, послідовності команд R. Такі файли мають розширення *.R (розширення файлу — це позначення його типу, яке визначає, які програми будуть з ним працювати; в операційній системі Windows розширення файлу може бути невидимим).
Пізніше буде корисно навчитися створювати файли RMarkdown. Ця вшита у R мова розмітки текстів та програмного коду дозволяє створювати такі сторінки, як ця: ті, що поєднують текстові пояснення, фрагменти коду та результати виконання цього коду. Файли RMarkdown мають розширення *.Rmd.
4.2 Перші кроки: вікна в RStudio та прості приклади команд в R
Відкриємо в RStudio скрипт (оберемо у такому випадку, що показаний на рис. 4.1.2, опцію R Script). Над консоллю у правій частині екрана з’явиться вікно редактору скриптів.
Напишемо і у цьому вікні найпростіший арифметичний вираз.
2*2
## [1] 4В файлі RMarkdown, де створюється даний текст, введена (в особливу вставку для програмних кодів, що називається чанком) лише команда, що була написана у вікні скриптів. Ви читаєте текст, що згенерував RMarkdown; до команди R у чанку він додав результат її виконання — те, що RStudio виводить у консолі.
Додамо у вікні скриптів ще кілька команд.
vect <- c(1:20, 100)
vect
## [1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
## [20] 20 100
?cПеред тим, як повторити команду, яку вона виконувала, консоль виводить символ >. Перед тим, як вивести результат, RStudio у квадратних дужках нумерує його елементи. Якщо вивід складається з одного числа, перед ним буде стояти [1]; якщо елементів більше, на початку кожного рядку буде позначатися номер першого елементу кожного рядку (це можна побачити на рисунку). Після кожної з команд ви бачите результат її виконання. Не відбилося у текстовому вигляді у документі, що згенерував RMarkdown, лише виконання команди ?c, втім, його можна побачити на рисунку (скрину екрана RStudio).
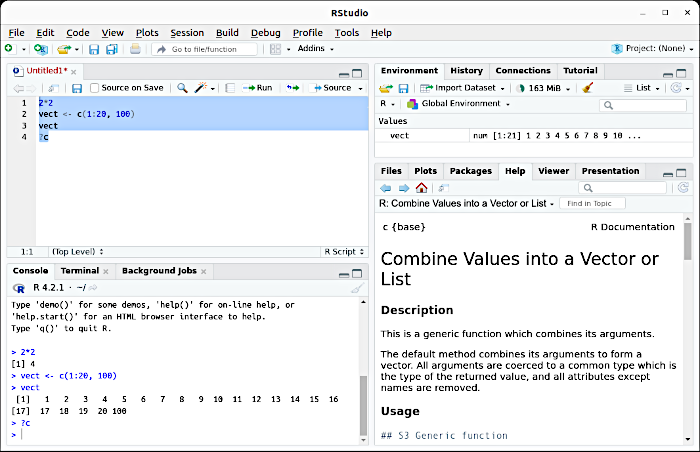
Рис. 4.2.1 Виділена у вікні скриптів послідовність команд була виконана кнопкою Run. Наслідки її виконання ми бачимо в усіх інших вікнах RStudio
Розглянемо рис. 4.2.1 детальніше. У вікні редактора скриптів (справа нагорі) ми бачимо команди, які були виконані.
Часто корисно виконувати скрипт покроково. Для виконання поточного рядку коду можна скористатися поєднанням клавіш Ctrl+Enter або кнопкою Run, що розташована у верхній частині вікна редактора. Код буде виконаний, і курсор переміститься на наступний рядок. Для виконання відразу декількох рядків (або частини рядка) треба виділити необхідний фрагмент і натиснути клавіші Ctrl+Enter або Run. Щоб виконати всі рядки скрипту, слід або виділити його цілком (Ctrl+A) і натиснути Run, або натиснути кнопку Sourse.
У вікні консолі (справа унизу) ми бачимо відповідь R на подані команди. Поруч з вікном консолі є й «роздільники» (як у паперовій теці), що дозволяють відкрити інші вікна, які зараз не є актуальними для нашого обговорення.
Зліва нагорі ми бачимо ще кілька роздільників; відкрито вікно середовища (Environment), де показані об’єкти, якими оперує R.
Зліва внизу — ще кілька «роздільників»; відкрито вікно допомоги (Help). Якби наші команди, введені у вікні скриптів, створювали б якусь діаграму, у нас було б відкрито вікно діаграм (Plots).
Ctrl+1 — переміщує курсор у вікно редактора скриптів; Ctrl+2 — переміщує курсор в консоль; Ctrl+L — очищає вікно консолі від тексту; Esc — перериває обчислення.
Панель історія (History) дозволяє переглянути історію команд, виділити деякі з них і відправити в консоль (To Console) або в редактор скриптів (To Source).
Проаналізуємо, що саме ми бачимо в цих вікнах. У другому рядку у редакторі скриптів ми ввели команду vect <- c(1:20, 100). Цією командою ми створили об’єкт, який має назву vect — цією назвою ми підкреслили, що цей об’єкт є вектором, базовим типом об’єктів для R.
Загалом, логіка роботи з R є такою. Ми створюємо певні об’єкти відповідними командами, а потім перетворюємо ці об’єкти та здійснюємо з ними різноманітні дії за допомогою наступних команд. Саме для цього нам потрібні скрипти — послідовності команд. Для того, щоб не заплутатися з тим, з якими об’єктами ми працюємо, дуже корисним є вікно Environment.
Створення або перебудова об’єктів відбувається з використанням символу привласнення: <- (спрацює і просто знак =, але його використання у такому випадку є в R «нестильним»). У випадку команди vect <- c(1:20, 100) відбувається створення об’єкта vect, якому привласнюється результат роботи функції c(). Вказана у попередньому реченні команда створює вектор vect; він з’являється у вікні Environment. А щоб «побачити» цей об’єкт в консолі, його слід викликати — просто назвати його ім’я.
Як узнати, що саме робить функція c()? Ввести у редакторі скриптів або у консолі команду ?c або help(c) (результат буде тій самий). Ця команда викличе у вікні Help детальний опис вказаної функції (звісно, англійською мовою). Функція c(), здається, єдина, назва якої складається з однієї літери. Вона об’єднує (combine або ж concatenate) певні об’єкти у вектор (або ж у список, list).
Зверніть увагу, як ми назвали цю функцію: c(). Крім її імені c, ми бачимо дужки, у яких мають бути вказані її аргументи. Аргументи функції c() — це ті об’єкти або величини (або інші функції!), які мають бути поєднані у створюваному об’єкті. Ці аргументи перелічуються через кому у тому порядку, у якому вони будуть поєднані.
Звісно, є функції, що використовуються без дужок, як-от арифметичні операції. Але це виключення. Деякі функції навіть не мають аргументів, але все одно застосовуються з дужками. Наприклад, команда: ls() виведе у консоль перелік об’єктів, які зараз активні у оточенні, Environment, програми. У дужки у такому випадку не треба нічого ставити, вони просто демонструють, що ми маємо справу з функцією. Сама по собі ця програма не є критично необхідною, адже на перелік об’єктів можна просто подивитися у вікні Environment. Втім, ця команда може стати частиною іншої, більш корисної команди. Команда rm(list = ls()) видаляє усе, що є в Environment. Це може бути дуже корисним, коли після розв’язання однієї задачі користувач R переходить до іншої, або в інших ситуаціях, коли об’єкти від попередніх розрахунків можуть заважати наступним.
Створюючи об’єкт vect ми поєднали результат роботи функції і окрему величину. Річ у тому, що символ : працює як функція: коли він розташований між двома числами, він вибудовує послідовність чисел між ними, що відрізняються одне від одного на одиницю.
Дослідимо, як працює ця команда.
6:12
## [1] 6 7 8 9 10 11 12Вибудувано послідовність натуральних чисел. А що буде, якщо спочатку буде розташовано більше число?
12:6
## [1] 12 11 10 9 8 7 6Працює. Початок та кінець ряду визначають, висхідний він або низхідний. А чи можна використовувати від’ємні числа?
-1:5
## [1] -1 0 1 2 3 4 5Можна. А чи можна використовувати нецілі числа? Перед тим, як це перевірити, зазначимо важливу деталь. В різних традиціях використовують різні символи для десяткових роздільників. На Заході частіше десятковим роздільником є крапка: 3/2=1.5. У кириличній традиції у цій ролі зазвичай використовують кому: 3/2=1,5. У R ніякого вибору нема: десятковий роздільник — крапка. Саме тому, якщо у такому разі використати команду 1,5:3, замість результату ви отримаєте повідомлення Error: unexpected ‘,’ in “1,”. Для R кома має розділяти різні елементи там, де це передбачено правилами!
1.5:5.3
## [1] 1.5 2.5 3.5 4.5Ми бачимо, що перше з чисел задає особливості ряду, а останнє визначає, скільки елементів ряду в ньому вміститься.
А якщо відстань між початком ряду та його кінцем менша за одиницю?
1.5:2.3
## [1] 1.5У такому разі ряд складатиметься з одного елемента.
А чи можна використовувати у команді арифметичні вирази? До речі, символ ^ позначає піднесення в ступінь.
2^3:(10+1)
## [1] 8 9 10 11Таким чином, команда vect <- c(1:20, 100) мала вибудувати послідовність натуральних чисел від 1 до 20, доєднати до них значення 100 та створити об’єкт (вектор) з назвою vect. Саме це ми і бачимо!
Додамо ще одне важливе зауваження. R вимагає чіткості та акуратності! Ви розумієте, чим відрізняються команди vect <- c(1:20, 100) та vect <- с(1:20, 100)? Скопіюйте їх та спробуйте виконати в R! Одна з них спрацює, а інша викличе повідомлення Error in с(1:20, 100) : could not find function “с”. Як ви думаєте, чому? А чому такі складнощі найчастіше виникають саме з функцією c?
У людини, яка починає працювати з R, з великою ймовірністю виникає типове питання. Як запам’ятати усі ці команди? Коли ви просунетеся у роботі з цим інструментом далі, ви впевнитеся, що ситуація зовсім не така жахлива, як може здаватися на початку. Найпростіші команди ви швидко запам’ятаєте, адже вам доведеться достатньо часто їх використовувати. З більш рідкісними або більш «накрученими» командами дещо складніше, але у цілому зовсім не трагічно. Важливо, щоб ви або пам’ятали, що якусь проблему можна розв’язати за допомогою якоїсь функції, або хоча б мали на це надію. Далі вам необхідно знайти зразок, зрозуміти, як він працює та переробити його під ваші власні потреби. Спочатку це здається складним, але кожного разу відбувається легше та легше. З часом у вас зберуться написані вами скрипти та їх чернетки, де буде зібрана колекція команд, що потрібні для розв’язання ваших задач. Чим далі ви просуватиметеся в опануванні R, тим легше вам буде робити наступні кроки.
4.3 Нашвидкуруч: приклад простих розрахунків з уведеними просто в R даними
У більшості випадків робота з R починається з того, що в нього завантажуються дані з якогось джерела (найчастіше — з електронних таблиць), але іноді цілком корисним може бути аналіз даних, уведених просто в R. Найчастіше це має сенс у разі, коли аналізуються відносно невеликі за обсягом дані. Наприклад, відносно невеликі за обсягом дані потрібні для використання χ2-тесту (chi-squared test, читається «хі-квадрат»), або тесту узгодженості Пірсона. Цей тест використовується для порівняння двох розподілів. Його зручно використовувати у разі, коли мова йде про розподіли по меристичним, ранговим або якісним (атрибутивним) ознакам (детальніше — див. пункт 1.6). У разі порівняння розподілів метричних ознак χ2-тест використовують, якщо порівнювані значення розбиті по певній кількості інтервалів, як у гістограмі.
Використаємо для прикладу дані, що були отримані студентами II курсу на навчально-польовій практиці на біологічній станції в Гайдарах). Дві студентки встановили склад вибірки з 230 зелених жаб, серед яких більшість складали самці. Студентки визначали, належать ці жаби до батьківського виду гібридогенного комплексу зелених жаб, Pelophylax ridibundus (позначення RR), чи до міжвидових геміклональних гібридів, Pelophylax esculentus, серед яких вирізняли диплоїдів (позначення 2n) та триплоїдів (3n). Ці три категорії жаб у даному контексті можна називати просто «формами».
Фактично, результати цього підрахунку можна виразити шістьма числами: чисельністю трьох зареєстрованих форм жаб серед самиць та самців. Ці дані нескладно напряму ввести у R.
Створимо два вектори: Forms (де перелічимо три форми зелених жаб, яких вирізняли у дослідженні) та Sexes (де перелічимо статі, які порівнювалися). Далі створимо матрицю Koryakov, в якій рядки відповідатимуть формам жаб, а стовпці — статям. Зрозуміло, що ця матриця матиме 6 комірок. Перелічимо зареєстровані кількості різних категорій жаб прямо у команді, якою створимо матрицю; врахуємо, що матриця заповнюється по стовпцях (спочатку перший стовпчик від першого рядка до останнього, потім — другий…).
Forms <- c( "RR", "2n", "3n")
Sexes <- c("Females", "Males")
Koryakov <- matrix(c(3, 10, 1, 5, 136, 9), nrow = length(Forms), ncol = length(Sexes), dimnames = list(Forms, Sexes))
Koryakov
## Females Males
## RR 3 5
## 2n 10 136
## 3n 1 9Чи відрізняється розподіл за формами жаб серед самиць та самців? Таке питання має важливий сенс — залежно від відповіді на нього, можна припустити, яку статеву хромосому, жіночу чи чоловічу несе геном відсутнього у басейні Сіверського Донця батьківського виду жаб, Pelophylax lessonae. В кожній категорії зареєстрована кількість самиць була меншою; може, зареєстровані відмінності розподілу статей за формами є просто наслідком випадковості?
Сформулюємо нульову та альтернативну гіпотези.
H0 — самиці і самці жаб в досліджуваній вибірці мають однаковий розподіл за формами, що позначені RR, 2n та 3n; зареєстровані відмінності у розподілах для двох статей є наслідком випадковості при формуванні вибірки.
H1 — самиці і самці жаб в досліджуваній вибірці відрізняються за розподілами за формами, що позначені RR, 2n та 3n.
Оберемо, яку саме гіпотезу ми приймемо, з використанням тесту χ2.
chisq.test(Koryakov)
## Warning in chisq.test(Koryakov): Chi-squared approximation may be incorrect
##
## Pearson's Chi-squared test
##
## data: Koryakov
## X-squared = 9.155, df = 2, p-value = 0.01028У цьому дослідженні, яке є пошуковим, ми приймаємо, що α, критичний рівень значущості, тобто ймовірність здійснити статистичну помилку першого роду та помилково прийняти альтернативну гіпотезу, коли вірною є нульова, дорівнює 0.05 (детальніше — у пункті 1.5). Ми отримали, що p-value = 0.0102899. Таким чином, встановлені з використанням χ2-тесту відмінності між розподілами самиць та самців зелених жаб за формами є значущими.
Втім, у використанні тесту χ2 у такому випадку є важливий недолік. Його використання є коректним, якщо очікуване значення у кожній комірці перевищує 5. Досліджена вибірка є недостатньо чисельною. У такому разі можна використовувати точний тест Фішера («Fisher’s exact test»).
fisher.test(Koryakov)
##
## Fisher's Exact Test for Count Data
##
## data: Koryakov
## p-value = 0.02096
## alternative hypothesis: two.sidedМи бачимо, що відмінності між розподілами лишилися значущими, хоча і не настільки, як у попередньому випадку: p-value = 0.02096.
У даному пункті ми не будемо обговорювати деталі використання тесту χ2 та точного тесту Фішера, адже тут ми просто обговорюємо особливості використання R у статистичних підрахунках. Так чи інакше, ми навели приклад аналізу даних, введених прямо у скрипт R.
4.4 До початку дослідження: визначення робочої директорії
Ми хочемо розглянути простий випадок використання R. Втім навіть у такому простому випадку бажано розглянути дії, які дуже часто доводиться виконувати на самому початку роботи. Ці дії слід обговорити дещо детальніше, ніж це необхідно для прикладу, що розглядається.
Під час певної сесії R він працює з певною директорією, текою на диску. Саме в тій теці він шукає файли, які відкриває (якщо йому не вказано конкретний шлях до іншої теки), саме в ній він зберігає створювані та службові файли. Якщо шлях до робочої теки не вказаний, R працює з кореневою директорію; це з багатьох поглядів є невдалим рішенням. Зручно, коли кожен окремий аналіз, що проводиться з використанням R, пов’язаний з окремою директорією. У такому разі слід створити у зручному місці директорію, де буде знаходитися файл з первинними даними для аналізу (чи, навпаки, вказати для R як робочу саме ту директорію, де знаходяться первинні дані).
Щоб вказати робочу директорію засобами RStudio, слід пройти наступним шляхом: Session / Set Working Directory / Choose Directory. Крім того, можна просто увести команду setwd(“PATH”) (у такому випадку “PATH” — це адреса потрібної теки, записана відповідно до правил операційної системи). Адресу директорії треба вказувати повністю, починаючи з фізичного або логічного диска у Windows або з материнської директорії у Linux.
Як узнати цю адресу? Спитати у R!
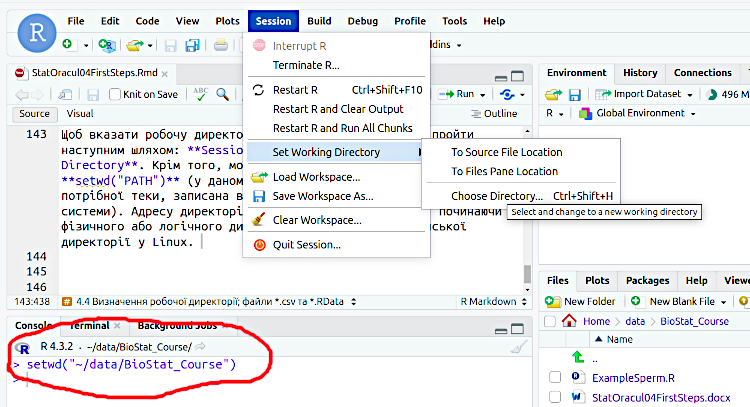
Рис. 4.4.1 Якщо ми змінимо робочу директорію засобами RStudio, у консолі з’явиться її адреса
Після того, як обрано нову робочу директорію, RStudio повідомить, яку саме команду воно виконало. Цю команду можна скопіювати і вставити у скрипт; у такому разі, при виконанні послідовності команд, що пов’язана з певним робочим простором, R буде відразу спрямовуватися у потрібне місце.
4.5 До початку дослідження: читання файлів .csv (і використання «ґраток»)
У типовому випадку R працює з первинними даними, які, найчастіше за все, збираються у якомусь іншому програмному забезпеченні. Далі їх треба перенести у R. Зазвичай, типовим «шлюзом» для перенесення даних між різними програмами є файли формату .csv, Comma-Separated Values. Фактично, це звичайний текстовий файл, де дані таблиці представлені у вигляді рядків. Окремі комірки таблиці при цьому відділяються певним знаком пунктуації (у типовому випадку це — коми).
Почнемо з простого випадку. На рисунку — електронна таблиця, де зібрані дані про довжину (у пікселях) сперматозоїдів п’яти різних самців гібридних жаб, Pelophylax esculentus.
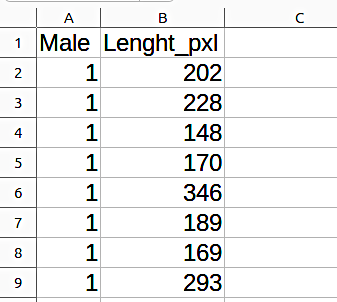
Рис. 4.5.1 Заголовок таблиці ExampleSperm, яку збережено у форматі .csv
Зберігаємо в електронних таблицях файл з вимірами сперматозоїдів як .csv, переносимо його у теку, з якою працює R. Тепер читаємо цей файл засобами R.
У наведеному далі фрагменті коду використаємо важливу особливість R-скриптів. В тексті самого скрипту можна використовувати коментарі, що позначаються «ґратками» (#). Коментарі можуть бути використані у робочому рядку після певного виконуваного тексту, як це зроблено у наступному прикладі в першому рядку. У такому разі, R виконує команди, що розташовані до «ґратки», ліворуч від цього символу, та ігнорує усе, що розташовано праворуч від #. «Ґраткою» можна прикрити й цілий рядок, якщо розташувати цей символ на початку рядка.
До речі, R дозволяє прикрити «ґраткою» будь-яку кількість рядків або, навпаки, зняти з початку рядків таки символи; для цього достатньо виділити певну кількість рядків та натиснути Shift+Ctrl+C.
setwd("~/data/BioStat_Course") # Ця адреса має сенс лише на компʼютері автора цього фрагменту тексту, D.Sh.
Sperm <- read.csv('ExampleSperm.csv') # Цей файл має бути розташований у робочій директорії!
# Подивитися структуру файлу Sperm:
str(Sperm)
## 'data.frame': 1188 obs. of 2 variables:
## $ Male : int 1 1 1 1 1 1 1 1 1 1 ...
## $ Lenght_pxl: int 202 228 148 170 346 189 169 293 123 139 ...
summary(Sperm) # Ще одна команда, яку можна використати для оцінки вмісту об'єкта з даними
## Male Lenght_pxl
## Min. :1.000 Min. : 51.0
## 1st Qu.:2.000 1st Qu.: 99.0
## Median :3.000 Median :127.5
## Mean :3.003 Mean :153.6
## 3rd Qu.:4.000 3rd Qu.:183.0
## Max. :5.000 Max. :516.04.6 Ще до початку: датафрейми, фактори, attach(), файли .RData
Як ми бачимо, в R з’явився об’єкт Sperm, де адекватно відбито структуру даних й заголовки стовпців (це наслідок використання атрибутів функції read.csv() за замовченням). Втім, в отриманому об’єкті слід зробити певні зміни. До речі, що це за об’єкт?
class(Sperm)
## [1] "data.frame"Об’єкт Sperm належить до класу dataframe. Це слово можна перекладати українською по-різному; ми будемо використовувати просто кальку, датафрейм. Це — таблиця з даними, що складається з векторів (лінійних послідовностей даних), які мають однакову довжину. У цьому датафрейм подібний до матриці, але має одну важливу особливість. У матрицях усі дані мають однаковий тип — наприклад, текстовий або числовий (детальніше — пізніше). У датафреймі різні вектори можуть містити дані різних типів (але кожен вектор — дані якогось певного типу). Наш випадок має бути саме таким.
У таблиці з вимірами довжини сперматозоїдів різних самців гібридних жаб два стовпці (що перетворилися на два вектори у складі датафрейма Sperm) є різними. Перший містить номер особини; це просто код, що розділяє дані у другому стовпці (векторі) на 5 груп. Другий результат вимірів. Це — просто число.
Щоб краще зрозуміти різницю між цими типами даних, можна замислитися про таке. Чи має сенс, припустимо, визначення того, наскільки один сперматозоїд довший за інший? Звісно! Ми можемо відняти одне значення довжини сперматозоїда від іншого та вирахувати різницю між ними. А чи має сенс вираховування різниці між номерами різних особин? Ні! Для першого стовпця та вектора має значення лише те, однакові ці коди або різні. У такому разі ми маємо запланувати детально обговорити різноманіття типів об’єктів та типів даних у R, а зараз просто відбити цю різницю у датафреймі Sperm.
Ми вже встановили тип даних у обох векторів у складі датафрейма Sperm — подивіться на результат виконання команди str(Sperm): обидві змінні у цьому об’єкті мають позначку int, тобто integer. Як буде більш детально обговорено далі, це — позначення простого числового формату, дані у якому можуть бути виражені будь-яким числом. До речі, у результатах виконання цієї команди ми можемо побачити, як слід називати окремі вектори у складі датафреймів: перед назвою вектора там стоїть символ долара. Наприклад, подивимося на початок першого вектору.
head(Sperm$Male)
## [1] 1 1 1 1 1 1Ми отримали перші п’ять значень обговорюваного вектора; функція head() за умовчанням виводить саме таку кількість. А якби нас цікавила інша кількість значень? Слід вказати цю кількість як атрибут функції head(); ви вже знаєте, що типовий спосіб додавання атрибутів — вказати їх у команді після коми.
head(Sperm$Male, 10)
## [1] 1 1 1 1 1 1 1 1 1 1А чи слід кожного разу повторювати назву датафрейму, адже зрозуміло, що ми звертаємося кожного разу саме до нього? Можна і не повторювати, але доведеться вказати R, де саме слід шукати об’єкти Male та Lenght_pxl. Для цього слід використати функцію attach().
attach(Sperm)Тепер ми можемо звертатися до векторів у складі датафрейму Sperm напряму; впевнимося у цьому на прикладі функції tail(), що цілком аналогічна розглянутій функції head(), але виводить у консолі останні елементи вказаного об’єкту.
tail(Male, 12)
## [1] 5 5 5 5 5 5 5 5 5 5 5 5Як повідомити R, що дані у векторі Male мають інший тип, ніж у векторі Lenght_pxl (де дані дійсно мають належати до типу integer)? Перетворити перший вектор на фактор, тобто вектор, що приймає значення з чітко визначеного набору можливих даних і може бути використаний для поділу даних на групи.
Sperm$Male <- factor(Sperm$Male)Ми виконали зміну об’єкта завдяки функції привласнення <-. Логіка тут така: Новий_стан <- функція(Старий_стан). Ми можемо впевнитися, що тип даних у першому векторі змінився.
str(Sperm)
## 'data.frame': 1188 obs. of 2 variables:
## $ Male : Factor w/ 5 levels "1","2","3","4",..: 1 1 1 1 1 1 1 1 1 1 ...
## $ Lenght_pxl: int 202 228 148 170 346 189 169 293 123 139 ...Тепер вектор Male перетворився на вектор, що приймає 5 різних значень — те саме, що ми мали отримати!
Може бути так, що ми будемо звертатися до датафрейму Sperm у різних R-скриптах? Звісно. І кожного разу читати .csv-файл, перетворювати перший вектор на фактор та робити усі інші зміни, які можуть знадобитися? Можна й так; достатньо лише повторювати раз за разом відповідну послідовність рядків у R-скриптах. Але є й інше рішення: зберегти потрібний об’єкт R у вигляді окремого файлу, до якого можна буде звертатися пізніше.
save(Sperm, file = "SpermatozoaLength.RData")Ця команда збереже файл з розширенням .RData у робочу директорію, з якою працює R; за необхідності можна вказати і іншу необхідну адресу, як-от save(Sperm, file = “/home/dsh/!_Courses/BioStatistica/SpermatozoaLength.RData”).
Отриманий файл можна буде у будь-який момент прочитати. У разі файлу .RData, що розташований у робочій директорії, це можна зробити наступною командою.
load("SpermatozoaLength.RData")4.7 І ще до початку: проблеми з десятковими роздільниками та кодуванням в .csv-файлах
Чи завжди робота з .csv-файлами є такою простою, як у наведеному прикладі з файлом ExampleSperm.csv? На жаль, ні. Наприклад, поширеною є проблема, що пов’язана з використанням різних десяткових роздільників. Наприклад, в одному з попередніх розділів вже було наведено посилання на файл PelophylaxExample.csv. Там результати вимірів жаб вказані з точністю до мм, а як десятковий роздільник використано кому. Якщо ми спробуємо прочитати його так само як попередній файл, командою PE <- read.csv(‘PelophylaxExamples.csv’), R повідомить про помилку: “Error in read.table(file = file, header = header, sep = sep, quote = quote, : more columns than column names”. Логічно: файл має певну кількість заголовків стовпців, а в рядках з даними ті значення, що містять всередині кому, R розуміє як два різні значення! Що ж робити?
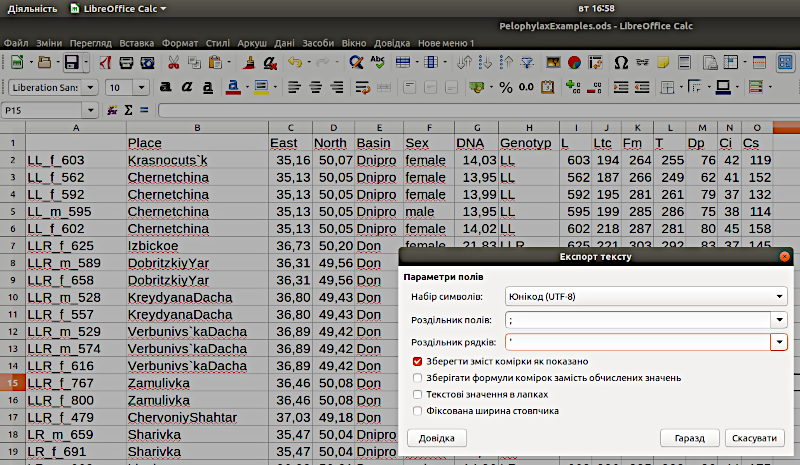
Рис. 4.7.1 Файл у форматі .csv слід зберігати так, щоб R міг його «зрозуміти»
Як показано на рисунку, під час збереження файлів .csv слід не використовувати коми як символи, що розділяють полі (комірки) та рядки. У такому разі цей файл можна буде прочитати, якщо вказати R, як саме його слід розуміти.
PE <- read.csv('PelophylaxExamples.csv', sep = ";", dec = ",") # Цей файл має бути розташований у робочій директорії!Файл .csv прочитано. Результат читання цього файлу збережено у датафреймі PE. Подивимося, що у нас вийшло!
head(PE)
## Code Place East North Basin Sex DNA Genotyp Lc Ltc Fm
## 1 LL_f_603 Krasnocuts`k 35.16 50.07 Dnipro female 14.03 LL 60.3 19.4 26.4
## 2 LL_f_562 Chernetchina 35.13 50.05 Dnipro female 13.95 LL 56.2 18.7 26.6
## 3 LL_f_592 Chernetchina 35.13 50.05 Dnipro female 13.99 LL 59.2 19.5 28.1
## 4 LL_m_595 Chernetchina 35.13 50.05 Dnipro male 13.95 LL 59.5 19.9 28.5
## 5 LL_f_602 Chernetchina 35.13 50.05 Dnipro female 14.02 LL 60.2 21.8 28.7
## 6 LLR_f_625 Izbickoe 36.73 50.20 Don female 21.83 LLR 62.5 22.1 30.3
## Ti Dp Ci Cs
## 1 25.5 7.6 4.2 11.9
## 2 24.9 6.2 4.1 15.2
## 3 26.1 7.9 3.7 13.2
## 4 28.6 7.5 3.8 11.4
## 5 28.1 8.0 4.5 15.8
## 6 29.2 8.3 3.7 14.5Як і у випадку попереднього файлу, деякі ознаки, які R прочитав як прості текстові ознаки, є факторами. Чи вважати фактором ознаку Place — відкрите питання. З одного боку, місця збору зразків можуть бути різними, і їхній вичерпний перелік може бути неможливим. З іншого боку, можлива ситуація, коли жаби з одного оселища порівнюються з жабами з іншого оселища. У такому разі, ознаку Place слід розглядати як фактор. Відносно ознак Basin, Sex та Genotyp сумнівів нема — це фактори.
attach(PE)
Basin <- as.factor(Basin)
Sex <- as.factor(Sex)
Genotyp <- as.factor(Genotyp)
save(PE, file = "PelophylaxExamples.RData")Зазвичай, перший рядок таких таблиць, як ті, з якими ми працюємо, містить назви стовпців. За умовчанням R враховує ці заголовки. А коли заголовків нема, може бути потрібним використати аргумент OBJECT <- read.csv(‘FILENAME.csv’, …, header =FALSE).
До речі, певні труднощі можуть виникати при читанні файлів, де використовувалася кирилиця (найпростіше рішення — не використовувати її в статистичних файлах загалом!). Коли кирилиця читається неправильно (замість з дитинства знайомих літер, що заспокоюють та викликають довіру, — «козявушки», вони ж «кракозябри», що травмують нашу психіку самим своїм виглядом), слід встановити, з яким кодуванням було збережено файл .csv та вказати необхідне кодування окремим атрибутом, наприклад OBJECT <- read.csv(‘FILENAME.csv’, sep = “SIMBOL”, dec = “SIMBOL”, encoding = “UTF-8”) або OBJECT <- read.csv(‘FILENAME.csv’, encoding = “Windows-1251”).
Зверніть увагу! Як це зроблено у попередній команді, ім’я файлу слід вводити з одинарними прямими лапками, а символи, які треба використовувати як розділювачі, — брати у подвійні прямі лапки. Загалом, важливим джерелом помилок, які можуть перешкоджати роботі в R, є плутанина з подібними один на одного символами. Наприклад, причиною колізії, що обговорюється наприкінці пункту 4.2, є використання замість літери c з латиниці літери с з кирилиці (вони знаходяться на клавіатурі в одному місці та майже не відрізняються одна від одної, і тому їх дуже легко переплутати). Дещо подібний комплекс проблем пов’язаний і з лапками. Наприклад, якщо ви напишете так: sep = “;”, R просто нічого не зрозуміє. Подвійні (як і одинарні) лапки повинні бути прямими, тобто такими, які в найбільш поширеній розкладці ставляться при натисканні клавіші, що відповідає за українську літеру «Є» або російську — «Э» (до речі, ось приклад третього типу лапок). Щоб R виконав команду, треба писати виключно sep = “;”. На щастя, ви можете побачити, чи «розуміє» вас RStudio. Якщо RStudio приймає синтаксис введеного тексту, він підсвічує назви файлів, роздільники і інші елементи набраного користувачем тексту.
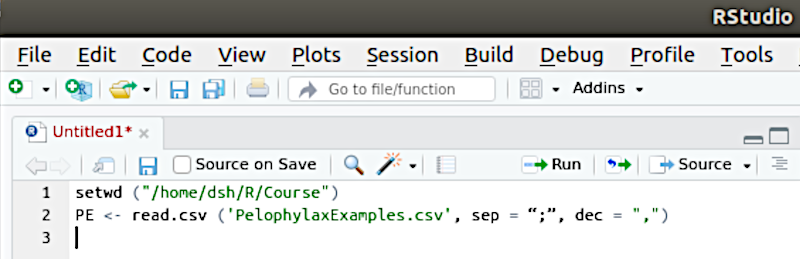
Рис. 4.7.2 «Підсвічування» елементів тексту в RStudio: у другому рядку ім’я файлу і знак десяткового розділювача (dec) підсвічені зеленим, а знак розділювача комірок (sep) — ні (там використано неправильні лапки)
Загалом, в RStudio є достатньо зручні засоби допомоги під час створення команд. Припустимо, ми плануємо роздивитися структуру створеного фрейму з використанням команди str(NAME). Під час набору назви функції RStudio у віконці, що спливає (хінті), запропонує варіанти, що починаються подібним чином, та виведе нагадування про властивості цих функцій. RStudio запропонує можливі варіанти продовження початого тексту під час зупинки у наборі або при натисканні клавіші Tab.
Рис. 4.7.3 Спливанні віконця в RStudio можуть бути дуже корисними; викликати підказку можна клавішею Tab
4.8 Перед самим початком: завантаження та ввімкнення необхідних пакунків та бібліотек
Опис об’єктів та функцій R організовано у пакунків. У дистрибутив R входить низка стандартних пакунків, як-от base, datasets, utils, gr-Devices, graphics, stats та **methods*)**. Цього набору достатньо для розв’язання величезної кількості задач. Але це не усе, що доступно користувачу R.
Джерелом нескінчених можливостей R є те, що, крім стандартних пакунків, його користувачі можуть використовувати величезну кількість додаткових. Пакунки можуть бути написані як на мові R, так і на інших мовах програмування; їх можна отримувати зі сховища і додавати до складу стандартного дистрибутиву R, що встановлюється під час інсталяції. Використання пакунків є причиною того, що хоча мова R є досить простою, її мінімальний набір можливостей може майже необмежено розширятися. Величезна кількість програмістів та вчених розробляють нові функції, що можуть бути реалізовані в R. На момент написання цього тексту у репозиторії (хранилищі) на офіційному сайті R було доступно 20539 пакунків. Їх доступний набір забезпечує виконання майже усіх статистичних процедур, що розроблені людством. Це — величезний результат роботи користувачів R по усьому світу!
Пакунки зберігаються та поширюються у складі бібліотек, library. Інформацію про пакунок можна отримати так: library(help=PACKAGE), де PACKAGE — назва пакунка. Дізнатися, які пакунки встановлено на комп’ютері, можна командою library(). Щоб додати пакунок, його потрібно спочатку завантажити командою install.packages(“PACKAGE”), а потім ввімкнути: library(PACKAGE). Зверніть увагу, що у першому випадку назву пакунку узято у лапки, а у другому — ні; неврахування такого роду деталей є поширеною причиною помилок у роботі R.
Як багато інших функцій, функція install.packages може використовуватися з необов’язковими атрибутами. Наприклад, якщо вказати install.packages(“PACKAGE”, dependencies = TRUE), у разі, якщо для нормальної роботи пакунка PACKAGE необхідні якісь інші пакунки, вони встановляться разом. Якщо спробувати звернутися до функції пакунка, який ще не інстальовано та не ввімкнено у системі, R видасть повідомлення про помилку.
У цьому курсі ми будемо користуватися комплексом пакунків tidyverse. Як з іншими пакунками, щоб використовувати можливості tidyverse треба один раз на певному комп’ютері виконати команду install.packages(“tidyverse”), а потім починати ті скрипти, де будуть використовуватися функції з цього комплексу, рядком library(tidyverse). Ця команда підвантажить наступні пакунки: ggplot2, що призначено для побудови графіків та візуалізації результатів; tibble, для роботи з тібблами, оновленою версією датафреймів; tidyr, для підтримки формату tidy data; readr, для читання файлів в R; purrr, для функціонального програмування; dplyr, для перебудови даних; stringr, для роботи з рядковими змінними; forcats, для роботи зі змінними-факторами.
У наступному пункті ми будемо використовувати графічний пакунок ggplot2. Його можна встановити як окремо, так і у складі tidyverse.
4.9 Типова логіка і нескладний приклад використання R у біостатистичному дослідженні
Як, скоріше за все, будуть використовувати R читачі цього тексту? Було проведено певне дослідження. Зібрані первинні дані. Ці первинні дані (згідно з запропонованим каноном, не забувайте про нього!) були зібрані чи то в паперовому журналі, чи то в електронних таблицях. Навіть у першому випадку їх з часом слід перевести у електронну форму, і це, скоріше за все, буде зроблене в електронних таблицях — Calc (зі складу вільного та безплатного LibreOffice), Excel (з пропрієтарного, тобто такого, що комусь належить, та платного MicrosoftOffice), або з пропрієтарних, але безплатних Google Sheets.
Зверніть увагу: формувати таблицю з первинними даними слід не аби як, а відповідно до канону, щоб подальший аналіз був ефективним!
На наступному кроці зібрані первинні дані слід передати у R. Як показано у попередньому пункті, це можна зробити з використанням файлу .csv. У разі, якщо у первинних даних використано кому як десятковий роздільник, зберігати .csv-файл необхідно так, щоб коми не використовувалися як роздільники даних, як це показано на рис. 4.7.1. Слід розташувати створений файл у робочу директорію, чи вказати до нього шлях у команді read.csv(). Втім, щоб файли R не з’являлися у тих місцях на диску, де вони будуть зайвими, краще починати з визначення робочої директорії та працювати безпосередньо в ній.
З високою ймовірністю доведеться зробити певні зміни у об’єкті, що отриманий за допомогою команди read.csv(). Ці зміни можуть стосуватися назв стовпців або рядків, розрахунку нових стовпців, перетворення певних векторів у фактори тощо. Після цього цілком логічним є зберегти отриманий об’єкт у вигляді файлу .RData.
У разі, якщо при аналізі будуть використовуватися якісь додаткові пакунки (наприклад ggplot2), слід перевірити, чи були вони інстальовані, а потім ввімкнути. Оскільки інсталяція проходить один раз, відповідну команду у скрипті є сенс прикрити «ґраткою», щоб не витрачати при кожному запуску скрипту час та інтернет-трафік на завантаження вже інстальованого пакунка.
Описані кроки пояснені в цьому розділі та вже частково виконані в ньому; втім, для більшої наочності, їх можна повторити й тут.
# setwd("~/data/BioStat_Course") # Це - визначення робочої директорії у D.Sh.; у інших користувачів шлях має бути іншим
# install.packages("ggplot2") # На кожному локальному комп'ютері це слід виконати один раз
library(ggplot2) # Вмикати додаткові бібліотеки доведеться кожного разу
# Прочитати файл у форматі .csv, що було створено через "Збережено як..." у електронних таблицях та привласнити йому ім'я Sperm:
Sperm <- read.csv('ExampleSperm.csv') # Цей файл має бути розташований у робочій директорії!
Sperm$Male <- factor(Sperm$Male) # Перший стовпчик перетворюється на фактор
save(Sperm, file = "SpermatozoaLength.RData") # Збереження зміненого датафрейма у файл
# load("SpermatozoaLength.RData") # Якщо ви повернетеся до аналізу іншого разу, можна буде виконати це, а не три попередні рядкиЧому визначення робочої директорії закрито «ґраткою»? Щоб ви могли скопіювати код та запустити його на своєму комп’ютері. Оберіть шлях, що відповідає вашим умовам, визначте його, як показано на рис. 4.4.1, вставте на відповідне місце та приберіть «ґратку»!
Наступний типовий крок аналізу — візуалізація даних. У цьому випадку ми (без детального обговорення) використаємо розрахунок густини ймовірності для розподілів сперматозоїдів за довжиною. Річ у тому, що в наших даних є певний набір зареєстрованих вимірів сперматозоїдів кожної особини. Це — спостережуваний факт. Подивимось на гістограму, де поєднаємо усі досліджені нами 1188 сперматозоїдів.
qplot(Lenght_pxl, data = Sperm, geom = "histogram",
xlab = "Довжина сперматозоїда (пікселів)", ylab = "Кількість",
main = "Загальний розподіл довжини сперматозоїдів 5 самців") 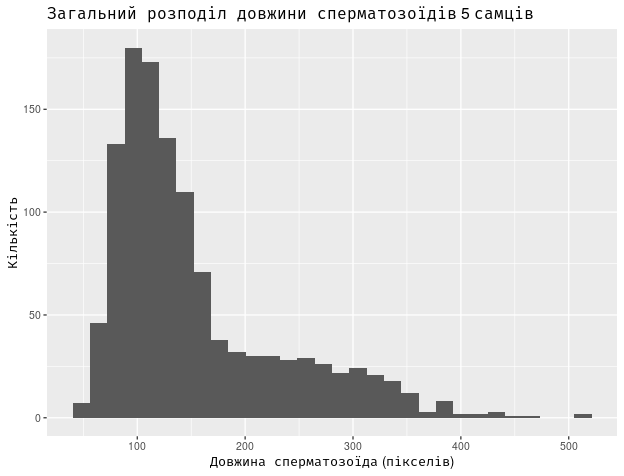
Рис. 4.9.1 Результат виконання попередньої команди
Використано команду, що використовує можливості пакунка ggplot2. Деталі цієї команди можна обговорити пізніше. Зараз важливо, що вона визначає, який вектор з якого об’єкту слід відбити на діаграмі, який тим цієї діаграми (гістограма), як підписати вісі та зображення у цілому. Ви бачите, як побудована команда: спочатку ми повідомлюємо R, що слід побудувати діаграму, а потім уточнюємо деталь за деталлю, додаючи необхідні атрибути цієї команди.
На гістограмі показано, скільки сперматозоїдів певної довжини ми зареєстрували. А тепер ми можемо доручити R розрахувати, якою є ймовірність потрапляння сперматозоїда у певний інтервал довжини. Ця функція має назву густини ймовірності. І порахуємо ми густину ймовірності для кожного самця жаби окремо. Щоб показати це на одній діаграмі, використаємо прозорість кожного шару, що відповідає певному самцю (це забезпечує атрибут alpha).
qplot(Lenght_pxl, data = Sperm, geom = "density",
fill = Male, alpha = I(1/5),
xlab = "Довжина сперматозоїда (пікселів)", ylab = "Ймовірність",
main = "Густина ймовірності довжини сперматозоїдів для 5 самців")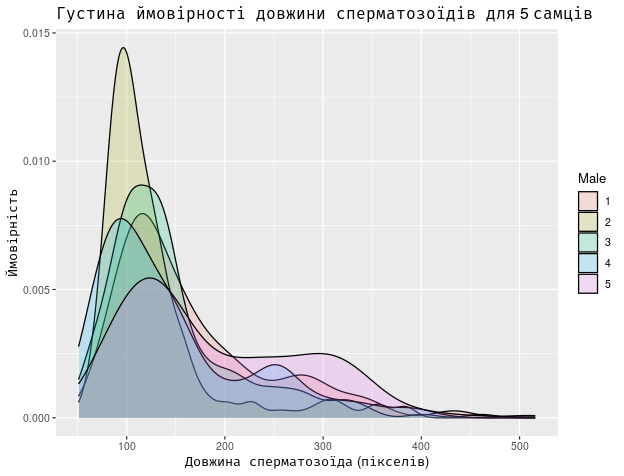
Рис. 4.9.2 Результат виконання попередньої команди
Що ми побачили на наведеному графіку? Головне — те, що різні самці мають різні розподіли сперматозоїдів за довжиною. Привертає увагу те, що розподіл сперматозоїдів за довжиною не дзвоноподібний за формою. З використанням специфічного статистичного жаргону можна сказати, що ці розподіли мають «важкий правий хвіст», тобто підвищену кількість більших значень. Як ми бачимо, у багатьох особин є другий пік розподілу, що відповідає набагато довшим сперматозоїдам.
Як ми можемо перевірити ті висновки, що зробили на підставі вигляду розподілів?
Згідно з центральною граничною теоремою статистики сума випадково розподілених величин збігається з нормальним розподілом. Наслідком цього є те, що величина, на значення якої впливає багато порівнюваних за силою факторів набуває розподілу. Якщо ми доведемо, що розподіл сперматозоїдів за довжиною суттєво відрізняється від нормального, ми встановимо, що на довжину впливають якісь суттєві впливи, що відхиляють розподіл від нормального.
В цьому розділі (у пункті 4.3) ми використовували для порівняння розподілів за якісними або розбитими на певні діапазони ознаками тест узгодженості Пірсона χ2, або точний тест Фішера. У випадку довжини сперматозоїдів ми можемо вважати, що маємо справу з метричною ознакою (насправді, вона також виміряна з точністю до одного пікселя на фотографії, але поділ розподілу на такі невеликі відтінки не є для нас принципово важливим). У такому разі можна використовувати тест Колмогорова-Смирнова. У разі, якщо проводиться порівняння розподілу з нормальним, крім Колмогорова-Смирнова, можна використовувати тест Шапіро-Вілка на нормальність.
Спочатку порівняємо розподіл всієї сукупності сперматозоїдів, що були виміряні, з нормальним розподілом.
Почнемо з тестом Колмогорова-Смірнова. Тут нам треба вказати, по-перше, величину, розподіл якої нас цікавить, і, по друге, з яким розподілом ми його будемо порівнювати. Нормальний розподіл позначається у такому випадку “pnorm”.
ks.test(Sperm$Lenght_pxl, "pnorm")
## Warning in ks.test.default(Sperm$Lenght_pxl, "pnorm"): ties should not be
## present for the Kolmogorov-Smirnov test
##
## Asymptotic one-sample Kolmogorov-Smirnov test
##
## data: Sperm$Lenght_pxl
## D = 1, p-value < 2.2e-16
## alternative hypothesis: two-sidedРізниця є дуже великою, p-value < 2.2e-16. Що таке 2.2e-16? Це запис експоненціальний запис (scientific notation), який автоматично використовується, коли R має справу з дуже дрібними значеннями. Можна було написати 0.00000000000000022, а можна — 2.2×10^-16, або, у спрощеному вигляді, 2.2e-16. Звісно, другий спосіб зручніше (користувачеві, як мінімум, не доведеться рахувати кількість нулів). Ця надзвичайно мала величина є ймовірністю того, що такий розподіл, який ми аналізуємо, отримано з нормального розподілу внаслідок випадковості при формуванні вибірки. Звісно, таке припущення можна відкинути як вкрай малоймовірне.
Порівняти розподіл, що нас цікавить, з нормальним, можна й з використанням тесту Шапіро-Вілка. Цей тест порівнює розподіл досліджуваної величини з нормальним, і тому вказувати саме нормальний розподіл в атрибутах цієї команди нема потреби.
shapiro.test(Sperm$Lenght_pxl)
##
## Shapiro-Wilk normality test
##
## data: Sperm$Lenght_pxl
## W = 0.85283, p-value < 2.2e-16Ми отримали те ж саме. Так або інакше, ми встановили, що на розподіл сперматозоїдів за довжиною впливають якісь суттєві чинники, що роблять його ненормальним.
Інший результат, який можна побачити за отриманими нами індивідуальними кривими густини ймовірності довжини сперматозоїдів — те, що вони різні для різних особин. Чи випадкова ця різниця? Один зі способів впевнитися в тому, що різниця є значущою — порівняти розподіли для двох особин, наприклад для 1-го та 2-го самців.
Слід зазначити, що порівнювати кожного самця з кожним — не найкраща ідея. Загалом можливо буде провести 4+3+2+1=10 порівнянь (1-го — з 2-м, 3-м, 4-м, 5-м, 2-го - з 3-м тощо…). У такому разі стане актуальна проблема множинних порівнянь, що детальніше розглянута у пункті 9.11. Тут зазначимо, що у разі 10 порівнянь значущою (у разі використання поправки Бонфероні) можна вважати різницю, для якої p<0.005.
Так або інакше, проведемо порівняння для першої пари самців. Для цього вкажемо тесту Колмогорова-Смирнова, які саме розподіли слід порівнювати.
ks.test(Sperm$Lenght_pxl[which(Sperm$Male==1)], Sperm$Lenght_pxl[which(Sperm$Male==2)])
## Warning in ks.test.default(Sperm$Lenght_pxl[which(Sperm$Male == 1)],
## Sperm$Lenght_pxl[which(Sperm$Male == : p-value will be approximate in the
## presence of ties
##
## Asymptotic two-sample Kolmogorov-Smirnov test
##
## data: Sperm$Lenght_pxl[which(Sperm$Male == 1)] and Sperm$Lenght_pxl[which(Sperm$Male == 2)]
## D = 0.31384, p-value = 7.868e-11
## alternative hypothesis: two-sidedРізниця значуща, з великим запасом!
Зверніть увагу, якою була логіка даного дослідження. Первинні дані → об’єкт R → візуалізація → припущення → перевірка припущень за допомогою статистичних тестів. Це — цілком типова логіка біостатистичного дослідження.
