 |
||||
|
← |
Д. Шабанов, М. Кравченко. «Статистичний оракул»: аналіз даних в зоології та екології |
→ |
||
|
Порівняння вибірок в R |
|
|||
|
«Статистичний оракул»-07 |
«Статистичний оракул»-10 |
|||
Тема 9 Порівняння вибірок в R
9.1 У яких ситуаціях виникає необхідність у порівнянні вибірок?
Значна частина статистичних досліджень відповідає одній простій схемі. Дуже часто необхідно встановити, до однієї генеральної сукупності належать дві вибірки, або до різних. Наведемо приклади таких досліджень.
— Зібрано вибірки певних тварин із низки точок. Слід визначити, чи є між ними суттєва різниця, що дозволяє говорити, що вони належать до різних форм (видів тощо). Питання можна переформулювати й так: ці вибірки належать до однієї генеральної сукупності, чи до різних?
— Чи впливає стать особин на довжину їх хвостів (тобто чи відрізняються особини різної статі за довжиною хвостів)? Інше формулювання проблеми: чи можна вважати, що значення даної ознаки в особин різної статі є вибірки з різних генеральних сукупностей (хвостів самок і хвостів самців) або їх можна розглядати як вибірку з однієї сукупності (хвостів особин даного виду без урахування їх статі)?
— Як впливає на певну ознаку якийсь фактор (наприклад, чи однаковою є виживаність експериментальних тварин у чистій воді та в суміші чистої води з водопровідною водою)? Чи є вибірки експериментальних тварин, що розвивалися у чистій та досліджуваній воді, вибірками з різних сукупностей?
— Чи покращують нові ліки стан хворих порівняно зі станом тих, хто, страждаючи на такі ж хвороби, отримує традиційне лікування? З однієї чи різних генеральних сукупностей отримано вибірки хворих, яких лікували традиційно та новими методами?
Отже, за складом вибірок слід зрозуміти, з однієї генеральної сукупності або різних вони взяті. Таке порівняння цілком відповідає жартівливому прикладу, використаному під час обговорення поняття статистичної значущості у першій темі.
9.2 Порівняння вибірок за Стьюдентом
У 1908 році англійський математик Вільям Госсет (рис. 9.2.1), який працював у пивній компанії та публікував свої роботи під псевдонімом Стьюдент, описав функцію, за якою значення вибіркової середньої розподілені навколо значення середньої генеральної сукупності. Компанія Гіннес, де працював Госсет, забороняла своїм працівникам оприлюдювати результати, які були отримані у ході виробничої діяльності, і тому Госсету довелося використати псевдонім. Для вибірок розподілу вибіркових середніх носять нормальний характер, а маленьких вибірок — є більш пологими, згладженими.

Рис. 9.2.1. Вільям Госсет (1876–1937), який працював під псевдонімом Стьюдент. Фото зроблено у 1908 році, коли він оприлюднив свій головний для історії науки результат
Користуючись цією функцією, можна визначити, якою є ймовірність того, що дві вибірки взяті з однієї генеральної сукупності, що має нормальний розподіл. При цьому обчислюється t -критерій або критерій Стьюдента. 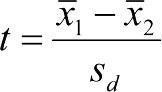 . У цій формулі в чисельнику стоїть різниця середніх, а в знаменнику — помилка цієї різниці.
. У цій формулі в чисельнику стоїть різниця середніх, а в знаменнику — помилка цієї різниці.
При рівні кількості об'єктів у вибірках(n1 = n2 = n) обчислення помилки різниці середніх виявляється простішим, ніж у наступному випадку; у загальному випадку вона обчислюється як корінь із суми квадратів стандартних відхилень порівнюваних вибірок:
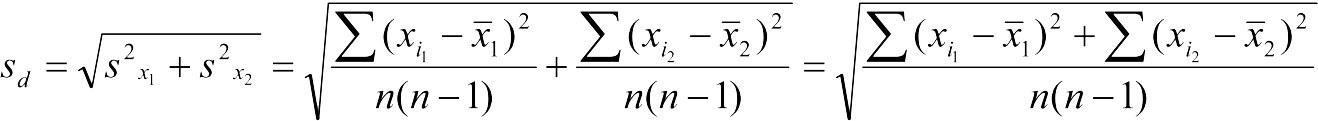 .
.
Якщо чисельності порівнюваних вибірок різні, тоді 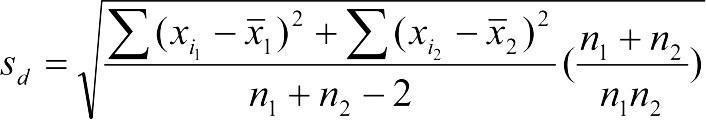 .
.
Для кожної кількості ступенів свободи df (df = n1 + n2 - 2) критерій Стьюдента набуває тим вищих значень, чим істотніші відмінності між вибірками. Їх порівнюють із табличними значеннями та визначають рівень статистичної значущості зареєстрованих результатів.
Розглянемо приклад такої таблиці (табл. 9.2.1).
Таблиця 9.2.1. Критичні значення t-критерію Стьюдента за різних рівнів статистичної значущості
|
Кількість ступенів свободи df |
p |
Кількість ступенів свободи df |
p |
||||
|
0,05 |
0,01 |
0,05 |
0,05 |
0,01 |
0,001 |
||
|
1 |
12,71 |
63,66 |
64,60 |
4 |
2,78 |
4,60 |
8,61 |
|
2 |
4,30 |
9,92 |
31,60 |
5 |
2,57 |
4,03 |
6,87 |
|
3 |
3,18 |
5,84 |
12,92 |
6 |
2,45 |
3,71 |
5,96 |
Отже, алгоритм «ручного» використання критерію Стьюдента дуже простий: для двох вибірок визначаються їх середні, обчислюється критерій Стьюдента, та за таблицями (для відповідного числа ступенів свободи) визначається рівень статистичної значущості зареєстрованих відмінностей.
Внаслідок своєї простоти критерій Стьюдента став використовуватися дуже широко, значно ширше, ніж слід було б. У будь-якому випадку, необхідно розібратися, як працює цей критерій.
9.3 Тест Стьюдента: порівняння двох вибірок
Порівняння вибірок за Стьюдентом можливо у разі виконання двох головних умов:
— перша умова: обидві вибірки походять з сукупностей, що мають нормальний розподіл;
— друга умова: дисперсії порівнюваних вибірок не мають відрізнятися.
У разі, якщо дисперсії відрізняються, використовують тест Стьюдента в модифікації Велча (Welch’s t-test). У разі, коли дисперсії дійсно є однаковими, «класичний» тест є дещо потужнішим, ніж Велч-тест. Поняття «потужність» у даному випадку — це здатність більш потужного тесту при певних умовах показати, що відмінності між вибірками є статистично значущими, у разі, коли менш потужний тест не дасть можливості зробити певний висновок. В R за умовчанням, без особливих повідомлень, використовується саме Велч-тест. Щоб вона використовувала традиційний варіант, до команди слід надати аргумент, де явно повідомити, що дисперсії порівнюваних вибірок є однаковими (дещо нижче наведено приклад).
Зверніть увагу: якщо ви використовуєте t-test у R, вам у типовому випадку не треба перейматися порівнянням дисперсій двох вибірок. Наприклад, ви встановили, що розподіл жаб за довжиною тіла близький до нормального. У такому разі ви маєте підстави для використання параметричного критерію. Чи треба визначити, наскільки відрязняється дисперсія за довжиною тіла, припустимо, для самиць та для самців? Скоріше за все, можна просто використати тест Стьюдента (точніше — Welch’s t-test). Хоча... Можна уявити собі таку ситуацію: самці мають близький до нормального роподіл за довжиною тіла, а самиці є або зовсім дрібними, або дуже великими. У разі, якщо частка самиць у вибірці є невеликою, їх розподіл (що дуже відрізняється від нормального) не дуже змінить розподіл вибірки у цілому. Подивитися на гістограму розподілу досліджуваної ознаки буде у будь-якому разі корисним.
Є різні варіанти використання тесту Стьюдента. Найпоширенішим з них є саме порівняння двох вибірок. Як його провести? По перше, просто вказати два порівнювані вектори. Структура нашої бази даних не дуже підходить для такого порівняння, але усе таки на ній це можливо показати.
Припустимо, ми завдалися питанням, чи значуще відрізняються довжина стегна від довжини гомілки у всієї сукупності досліджених нами жаб?
load("PelophylaxExamples.RData")
attach(PE)
t.test(Fm, Ti)
##
## Welch Two Sample t-test
##
## data: Fm and Ti
## t = -0.5776, df = 111.97, p-value = 0.5647
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -2.393944 1.313242
## sample estimates:
## mean of x mean of y
## 31.27018 31.81053Нагадаємо, що команда attach(PE) забезпечує пошук всередині датафрейму PE за назвами векторів у його складі. Якщо б її не було, ми б мали написати останню команду у такому вигляді: t.test(PE$Fm, PE$Ti).
Що ми бачимо в результатах виконання тесту Стьюдента (точніше, Велч-теста)? Перш за все, R чесно повідомлює, що використовує Welch Two Sample t-test.
Головне, що нас цікавить, це p-value, статистична значущість. p-value = 0.5647 — свідчення, що такі відмінності, як ті, що були зареєстровані між векторами Fm та Ti є такими, які виникають внаслідок випадковості між двома вибірками з однієї генеральної сукупності частіше, ніж у половині випадків. Різниця між довжиною стегна та гомілки є незначущою.
Що ще повідомлює функція t.test()? Значення t-критерію та кількість ступенів свободи (df). Кількість ступенів свободи є дрібною внаслідок використання Велч-теста. Якщо ми повідомимо, що дисперсії порівнюваних вибірок є однаковими, кількість ступенів свободи стане цілою.
t.test(Fm, Ti, var.equal = TRUE)
##
## Two Sample t-test
##
## data: Fm and Ti
## t = -0.5776, df = 112, p-value = 0.5647
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -2.393938 1.313236
## sample estimates:
## mean of x mean of y
## 31.27018 31.81053Те, що нульова гіпотеза полягає в тому, що середні двох вибірок є однаковими, зрозуміло (будемо сподіватися) і так. Альтернативну гіпотезу функція t.test() конкретизує: alternative hypothesis: true difference in means is not equal to 0, тобто вона полягає в тому, що середні сукупностей, з яких отримані вибірки, відрізняються.
Далі наведено 95% довірчий інтервал для різниці між середніми. З ймовірністю 95% різниця між середніми знаходиться у діапазоні від -2,4 до 1,3.
Останнє, що повідомлює R — середні значення досліджених вибірок. Наприкінці виводу сказано, що середнє значення довжини стегна — приблизно 31,3 мм, а довжини гомілки — 31,8 мм.
9.4 Спрямовані й неспрямовані гіпотези та двобічні й однобічні критерії (на прикладі тесту Стьюдента)
Як ви бачите, стегно виявилося у середньому коротшим за гомілку. Ми шукали значущі відмінності між цими відділами задньої кінцівки, і при цьому ми б вважали, що отримали результат і у тому разі, якщо б стегно виявилося б статистично значуще коротшим за гомілку, і у разі, якщо б воно виявилося статистично значуще довшим. Альтернативна гіпотеза, яку ми розглядали, була неспрямованою, і ми використовували двобічний критерій.
Можлива й інша ситуація, за якої ми б шукали аргументи на користь того, що стегно коротше за гомілку. В цьому прикладі причина такої постановки питання може буде не дуже зрозумілою, але є випадки, коли такі припущення природні. Припустимо, ми досліджуємо ліки, які прискорюють одужання. У такому разі ми будемо перевіряти гіпотезу, що хворі, які отримували ліки, хворіли менше, ніж ті, хто їх не отримували. Випадок, коли ліки збільшують термін одужання, для дослідника не цікавий. Така статистична гіпотеза є спрямованою, і у разі її висування використовують однобічні критерії.
Як це зробити?
t.test(Fm, Ti, alternative = "less")
##
## Welch Two Sample t-test
##
## data: Fm and Ti
## t = -0.5776, df = 111.97, p-value = 0.2823
## alternative hypothesis: true difference in means is less than 0
## 95 percent confidence interval:
## -Inf 1.011259
## sample estimates:
## mean of x mean of y
## 31.27018 31.81053Бачите? Альтернативна гіпотеза отримала інше формулювання: “alternative hypothesis: true difference in means is less than 0”; p-рівень став вдвічі меншим (0,28 замість 0,56).
Якщо б ми перевіряли гіпотезу, що перша вибірка є більшою, ми б використали аргумент alternative = "greater"; варіант за замовчуванням можна позначити alternative = "two.sided".
9.5 Тест Стьюдента: порівняння двох вибірок, що є частинами одного вектора
Ми використовували функцію t.test() для порівняння двох різних векторів (у розглянутому прикладі — Ti та Fm). Достатньо часто ми маємо справу з порівнянням двох груп випадків, що відрізняються за значенням певного фактора, за тією самою ознакою. Розглянемо простий приклад: встановимо довжину тіла самиць та самців за допомогою функції tapply().
Нагадаємо: tapply(X,INDEX,FUN =) — застосовує функцію FUN до кожної сукупності значень х, створеної відповідно до рівнів певного фактора; перелік факторів вказується за допомогою аргументу INDEX.
tapply(Lc, Sex, mean)
## female male
## 65.05806 64.26154У даному разі використаємо тій самий спосіб позначення «формул» для записи статистичних моделей, що був використаний при побудові рис.5.10.3. Як було там сказано, запис Lc ~ Sex має сенс: вплив на залежну змінну Lc групувальної змінної (предиктора) Sex.
t.test(Lc ~ Sex)
##
## Welch Two Sample t-test
##
## data: Lc by Sex
## t = 0.30585, df = 53.919, p-value = 0.7609
## alternative hypothesis: true difference in means between group female and group male is not equal to 0
## 95 percent confidence interval:
## -4.424899 6.017951
## sample estimates:
## mean in group female mean in group male
## 65.05806 64.26154Як ви можете побачити, самиці мають дещо більшу середню довжину тіла, ніж самці, але в цілому різниця є статистично незначущою — у повній відповідності до рис.5.10.3.
А що буде, якщо ми дамо команду t.test(Lc ~ Genotyp)? Нічого хорошого: R повідомить про помилку: Error in t.test.formula(Lc ~ Genotyp): grouping factor must have exactly 2 levels. Описаний спосіб порівняння вибірок працює лише у разі факторів, що приймають два значення. Саме тому команду t.test(Lc ~ Sex) виконано нормально, навіть якщо результатом виконання команди class(Sex) буде "character". Втім, можна перетворити змінну Sex на фактор: Sex <- as.factor(Sex).
9.6 Тест Стьюдента: порівняння середнього з певним значенням
В іншому варіанті t.test() досліджується одна вибірка, яка порівнюється з якимось значенням. Чи можемо ми вважати, що середнє значення довжини гомілки для усієї вивченої сукупності жаб дорівнює 30 мм, а відхилення від цієї величини (зареєстроване середнє — 31,3 мм) є випадковим?
Позначимо середнє вибірки як x̅, а середнє сукупності, з якої, можливо, отримана ця вибірка, як μ. У такому разі ми можемо записати нульову та альтернативну гіпотези так:
H0: x̅ = μ; H1: x̅ ≠ μ.
Як зробити вибір між цими гіпотезами? Вказати μ!
t.test(Ti, mu = 30)
##
## One Sample t-test
##
## data: Ti
## t = 2.7145, df = 56, p-value = 0.008807
## alternative hypothesis: true mean is not equal to 30
## 95 percent confidence interval:
## 30.47439 33.14666
## sample estimates:
## mean of x
## 31.81053Ні, різниця є статистично значущою; припущення, що середня довжина гомілки дорівнює 30 мм, можна відкинути. А як щодо припущення, що μ = 31?
t.test(Ti, mu = 31)
##
## One Sample t-test
##
## data: Ti
## t = 1.2152, df = 56, p-value = 0.2294
## alternative hypothesis: true mean is not equal to 31
## 95 percent confidence interval:
## 30.47439 33.14666
## sample estimates:
## mean of x
## 31.81053Підстав для відкидання нульової гіпотези (H0: x̅ = 31) недостатньо, різниця статистично незначуща.
9.7 Тест Стьюдента: парні порівняння (порівняння залежних вибірок)
Нагадаємо, що для сукупності жаб, яку ми розглядаємо, довжина стегна і гомілки відрізняються незначуще. Повторимо цей важливий результат:
t.test(Fm, Ti)
##
## Welch Two Sample t-test
##
## data: Fm and Ti
## t = -0.5776, df = 111.97, p-value = 0.5647
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -2.393944 1.313242
## sample estimates:
## mean of x mean of y
## 31.27018 31.81053Ми порівнювали дві вибірки, кожна по 57 зразків: 57 стегон та 57 гомілок. Порядок розташування зразків в цих вибірках не має значення. Перевіримо це — переплутаємо у випадковому порядку елементи у вибірках.
Fm
## [1] 26.4 26.6 28.1 28.5 28.7 30.3 29.0 30.6 25.7 25.1 25.8 26.3 31.6 34.9 38.9
## [16] 23.8 30.2 35.9 33.5 38.1 33.4 35.6 26.2 37.6 32.0 26.6 32.1 27.3 31.7 26.0
## [31] 28.8 31.5 32.8 33.8 33.0 35.2 35.3 23.1 28.3 41.1 28.8 31.6 35.9 32.6 25.9
## [46] 36.0 42.3 25.9 26.5 24.3 26.2 34.1 33.9 33.6 34.0 46.2 35.2
Random_Fm <- sample(Fm, 57)
Random_Fm
## [1] 30.2 30.6 26.2 37.6 24.3 31.5 35.2 29.0 33.9 32.8 36.0 25.9 32.6 26.6 32.0
## [16] 46.2 38.1 25.1 25.7 28.5 25.9 26.0 23.1 33.5 28.7 35.6 33.4 38.9 31.6 35.9
## [31] 27.3 26.5 25.8 30.3 26.4 28.8 35.3 23.8 32.1 42.3 31.7 26.6 31.6 28.1 35.9
## [46] 41.1 26.3 33.0 33.6 33.8 28.3 35.2 34.9 34.1 28.8 26.2 34.0
Ti
## [1] 25.5 24.9 26.1 28.6 28.1 29.2 27.7 30.4 24.6 25.7 26.2 26.7 29.8 34.6 37.6
## [16] 24.6 30.0 34.9 32.8 39.4 33.2 34.1 28.0 42.3 31.9 27.3 32.5 28.5 32.3 28.1
## [31] 28.9 31.9 34.5 36.4 33.4 35.6 34.4 24.8 29.3 37.2 30.2 34.1 35.9 36.2 27.7
## [46] 37.6 44.3 27.3 28.1 26.7 28.2 36.2 37.1 36.1 35.7 46.1 33.7
Random_Ti <- sample(Ti, 57)
Random_Ti
## [1] 27.7 34.5 33.4 34.9 37.1 29.3 28.5 30.4 24.6 26.7 26.7 34.6 29.2 34.1 26.2
## [16] 33.7 33.2 28.1 31.9 36.1 28.1 36.4 42.3 31.9 46.1 34.4 28.0 39.4 35.6 36.2
## [31] 34.1 30.0 37.6 37.6 44.3 35.7 24.9 28.2 35.9 32.5 30.2 28.1 24.8 25.7 26.1
## [46] 32.8 27.7 28.9 28.6 29.8 27.3 36.2 27.3 37.2 24.6 25.5 32.3
t.test(Random_Fm, Random_Ti)
##
## Welch Two Sample t-test
##
## data: Random_Fm and Random_Ti
## t = -0.5776, df = 111.97, p-value = 0.5647
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -2.393944 1.313242
## sample estimates:
## mean of x mean of y
## 31.27018 31.81053Насправді цей результат є тривіальним. Результат порівняння незалежних вибірок за Стьюдентом аніяк не залежить від розташування окремих спостережень в цих вибірках. Втім, цей порядок має вагоме значення, адже кожен рядок бази даних — це окрема особина. Спостереження в порівнюваних вибірках утворюють пари: одне значення відповідає довжині стегна, а інше — довжині гомілки певної особини.
Що буде, якщо ми порівняємо довжину гомілки та стегна у кожній окремій жаби? Використаємо парні порівняння!
t.test(Fm, Ti, paired = TRUE)
##
## Paired t-test
##
## data: Fm and Ti
## t = -2.5712, df = 56, p-value = 0.01282
## alternative hypothesis: true mean difference is not equal to 0
## 95 percent confidence interval:
## -0.9613451 -0.1193567
## sample estimates:
## mean difference
## -0.5403509У дослідженій сукупності жаб гомілка є статистично значущою, ніж стегно! Чи є у отриманих нами результатах якась суперечність? Ні. Такий результат є закономірним.
Роздивимося, як співвідносяться ці гомілки та стегна у кожній жаби. Використаємо функцію plot(), визначимо однакові діапазони осей, і проведемо лінію, яка відповідає рівним значенням довжини стегна та гомілки.
plot(Fm, Ti, xlim = c(23, 44), ylim = c(23, 44))
abline(a = 0, 1, col = "green") 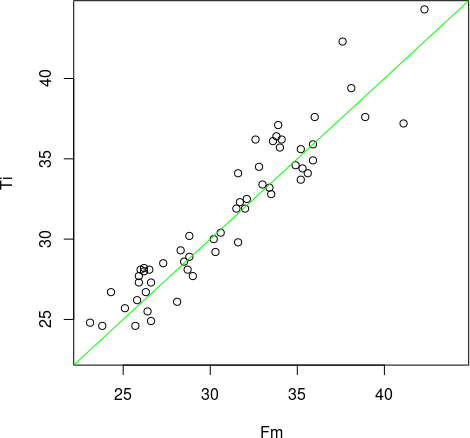
Рис. 9.7.1. Зелена лінія відповідає випадку Ti = Fm (у R слід було б написати «Ti == Fm»). Чи правда над цією лінією більше точкок, ніж під нею?
Нам здається, що над лінією розташовано більше точок, ніж під лінією, чи ні? Як це перевірити?
length(Ti[which(Ti>Fm)])
## [1] 35
length(Ti[which(Ti==Fm)])
## [1] 1
length(Ti[which(Ti<Fm)])
## [1] 21Так, дійсно, серед досліджених нами жаб більше таких, у яких гомілка довша за стегно. Якщо ми розглядаємо спільний розподіл першого та другого вимірів, зв’язок між ними здається достатньо слабким. Втім, коли ми переносимо увагу з сукупності у цілому до кожної окремої особини, ми можемо побачити, що гомілка частіше є довшою.
Фактично, парні порівняння перевіряють, чи відрізняється різниця між значеннями з двох вибірок, від 0. Перевіримо це.
Ti_minus_Fm <- Ti - Fm
t.test(Ti_minus_Fm, mu = 0)
##
## One Sample t-test
##
## data: Ti_minus_Fm
## t = 2.5712, df = 56, p-value = 0.01282
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## 0.1193567 0.9613451
## sample estimates:
## mean of x
## 0.5403509Тій самий результат, що у випадку парних порівнянь!
9.8 Непараметричні аналоги параметричних методів
Параметричні критерії, які ми розглядали досі, засновані на тому, що вибірки, що порівнюються, можна охарактеризувати двома параметрами: середнім і стандартним відхиленням (або якоюсь іншою мірою мінливості). А що робити, якщо розподіл у вибірках (чи, точніше, у тій генеральній сукупності, звідки були отримані ці вибірки) є зовсім іншим?
Якщо кількість кожної з порівнюваних вибірок досить велика (більше ніж 100), параметричні критерії можна використовувати однаково. Хоч би який розподіл мали ці вибірки, їх середні «поводяться» приблизно так само, як середні вибірок з нормальним розподілом. Однак, якщо кількість вибірок нижча, слід використовувати непараметричні критерії.
Наприклад, непараметричним аналогом t-критерію Стьюдента є U-критерій Манна-Уітні. Критерій Стьюдента побудований на основі розподілу, який описує відхилення середнього значення вибірки певної чисельності x̅ навколо генеральної середньої нормально розподіленої величини μ. Чим сильніше відхилення x̅ від μ, тим нижче ймовірність того, що воно вийшло через випадковість при формуванні вибірки. А як діяти, якщо ми нічого не знаємо про характер розподілу генеральних сукупностей?
Розглянемо досить простий приклад, який пояснює, як працює велика група непараметричних методів, — рангові критерії. Розглянемо приклад. У нас є дві вибірки. Розташуємо їх елементи у порядку зростання: перша — a1, a2, a3, a4, a5; друга — b1, b2, b3, b4, b5, b6. Складемо з елементів цих вибірок загальний ряд, побудований порядку зростання їх значень. Порівняємо три різні випадки:
№ 1: a1, a2, a3, a4, a5, b1, b2, b3, b4, b5, b6;
№ 2: a1, a2, a3, a4, b1, a5, b2, b3, b4, b5, b6;
№ 3: b1, a1, b2, a2, b3, a3, b4, b5, a4, a5, b6.
У разі № 1 усі елементи однієї вибірки розташовані з одного боку загального ряду, а всі елементи іншого ряду – з іншого боку. У разі № 2 однієї перестановки (елементів b1 і a5) було б достатньо, щоб порядок елементів став, як у випадку № 1. Нарешті, у разі № 3 елементи двох вибірок переплутані, і щоб побудувати їх у ряд, де спочатку стоятимуть одні, а потім – інші, треба зробити 5 перестановок. Нам потрібно вибрати між альтернативною гіпотезою (згідно з якою вибірки a і b взяті з різних сукупностей) і нульовою гіпотезою (згідно з якою ці вибірки взяті з однієї сукупності). Чи однакові ймовірності альтернативної та нульової гіпотез для показаних нами трьох різних випадків? Ні; альтернативна гіпотеза найімовірніша у першому випадку, а нульова — у третьому.
Ідея рангового непараметричного критерію полягає в тому, що ми можемо використовувати кількість необхідних перестановок як міру для оцінки нульової та альтернативної гіпотези. Конкретні величини, які обчислюються при застосуванні різних непараметричних критеріїв, виявляються різними, але логіка порівняння приблизно відповідає розглянутому нами прикладу.
Отже, завдяки застосуванню дотепних підходів для параметричних методів порівняння вибірок підібрано їх непараметричні аналоги (табл. 9.8.1). Найчастіше непараметричні методи мають меншу потужність (тобто частіше відкидають альтернативну гіпотезу в тій ситуації, коли вона насправді вірна), зате дозволяють працювати з різноманітно розподіленими даними і є менш чутливими до малої чисельності порівнюваних вибірок.
Таблиця 9.8.1. Непараметричні аналоги параметричних методів
|
Тип порівняння |
Параметричні методи |
Непараметричні методи |
|
Порівняння значень величини у двох незалежних вибірках |
t-критерій Стьюдента; Дисперсійний аналіз (ANOVA) |
U-критерій Манна-Уітні; Критерій серій Вальда-Вольфовіца; Двовибірковий критерій Колмогорова-Смирнова |
|
Порівняння значень величини у двох залежних вибірках |
t-критерій Стьюдента для парних порівнянь |
Критерій Вілкоксона; Критерій знаків |
|
Порівняння значень величини у кількох незалежних вибірках |
Дисперсійний аналіз (ANOVA) |
Ранговий дисперсійний аналіз Краскела-Уолліса; Медіанний тест |
9.9 Тест Вілкоксона (включно з тестом Манна-Вітні)
В R прийнято розглядати як тест Вілкоксона (Wilcoxon rank test) у його вузькому сенсі, як засіб порівняння пов’язаних вибірок, так і тест Манна-Вітні (Mann–Whitney U test) як засіб порівняння незалежних вибірок під єдиною назвою — як тест Вілкоксона. Річ у тому, що тест Вілкоксона був запропонований дещо раніше (у 1945 р.) ніж тест Манна-Вітні (1947 р.)
Цей тест допускає ті ж самі використання, що й тест Стьюдента. Подивимось.
Порівняння незалежних вибірок, кожна з яких представлена окремим вектором (тест Манна-Вітні).
wilcox.test(Ti, Fm)
##
## Wilcoxon rank sum test with continuity correction
##
## data: Ti and Fm
## W = 1741.5, p-value = 0.5091
## alternative hypothesis: true location shift is not equal to 0Парне порівняння.
wilcox.test(Ti, Fm, paired = TRUE)
##
## Wilcoxon signed rank test with continuity correction
##
## data: Ti and Fm
## V = 1105, p-value = 0.01239
## alternative hypothesis: true location shift is not equal to 0Результат подібний до того, що був отриманим за допомогою тесту Стьюдента.
У разі незалежних вибірок ми могли б використати аргумент paired = FALSE, але це не обов’язково, адже такий варіант приймається за замовченням.
Порівняння двох частин одного вектора, що відрізняються за значенням фактора.
wilcox.test(Lc ~ Sex)
## Warning in wilcox.test.default(x = DATA1L, y = DATA2L, ...): cannot
## compute exact p-value with ties
##
## Wilcoxon rank sum test with continuity correction
##
## data: Lc by Sex
## W = 431.5, p-value = 0.6537
## alternative hypothesis: true location shift is not equal to 0Одновибіркове використання. Перевіряється гіпотеза, що вибірка походить з сукупності, що рівномірна розподілена навколо значення μ.
wilcox.test(Ti, mu = 31)
##
## Wilcoxon signed rank test with continuity correction
##
## data: Ti
## V = 938.5, p-value = 0.3756
## alternative hypothesis: true location is not equal to 31
9.10 Тест Краскела-Волліса
Тест Краскела-Волліса (Kruskal-Wallis rank sum test) часто розглядають як непараметричний дисперсійний аналіз (детальніше дисперсійний аналіз ми будемо розглядати пізніше). Ключова особливість цього тесту полягає в тому, що він дозволяє порівнювати водночас кілька (більше за дві) групи. У разі, коли тест Краскела-Волліса застосовується для двох груп, він є ідентичним тесту Манна-Вітні.
Формат команди, що викликає цей тест, такий.
kruskal.test(Ti_Fm ~ Genotyp, data = PE)
##
## Kruskal-Wallis rank sum test
##
## data: Ti_Fm by Genotyp
## Kruskal-Wallis chi-squared = 20.238, df = 4, p-value = 0.0004481Оскільки ми раніше використали команду attach(PE), викликати тест Краскела-Волліса можна й простішою командою.
kruskal.test(Ti_Fm ~ Genotyp)
##
## Kruskal-Wallis rank sum test
##
## data: Ti_Fm by Genotyp
## Kruskal-Wallis chi-squared = 20.238, df = 4, p-value = 0.0004481Чи можна на підставі цього результату вказати, які саме пари груп відрізняються одна від одної, наприклад, чи відрізняються особини LLR від LRR? Ні. Якщо нас цікавить це питання, слід використовувати тест Мана-Вітні. А можна провести тест Мана-Вітні для усіх можливих пар генотипів? Ні; про це — у наступному пункті. А в тесті Краскела-Волліса, як і в дисперсійному аналізі, слід проводити так звані пост-хок тести (post hoc tests), які також можна називати апостеріорними тестами. Цю тему ми детальніше розглядатимемо у зв’язку з дисперсійним аналізом.
9.11 Проблема множинних порівнянь
А чому не можна було провести тести Мана-Вітні для усіх можливих пар генотипів? До речі, перелічимо усі ці пари: LL vs. LLR, LL vs. LR, LL vs. LRR, LL vs. RR, LRL vs. LR, LLR vs. LRR, LLR vs. RR, LR vs. LRR, LR vs. RR, LRR vs. RR — усього 10 пар. Насправді, можна, але висновок, що буде отриманий внаслідок такого аналізу, треба буде коригувати.
Згадаємо, про що свідчить статистично значуща різниця між двома порівняними вибірками? Що такі (або ще більші) відмінності, як між порівняними вибірками можуть виникати внаслідок випадковості при формуванні вибірок з однієї генеральної сукупності не частіше певного рівня ймовірності (α). Найчастіше в пошукових біологічних дослідженнях вважають, що α=0.05, тобто 1/20. Якщо ймовірність випадкового виникнення таких відмінностей між вибірками, що ми зареєстрували, складає одну двадцяту, ми набагато скоріше помилимося, якщо будемо вважати відмінності між вибірками випадковими (у разі, якщо вони є насправді), ніж у разі, якщо ми вирішимо, що зареєстрували відмінності, а ці вибірки насправді не відрізняються.
Ми вважаємо значущими відмінності, які «самовільно» виникають не частіше, ніж у одному випадку на 20 спроб… А якщо ми зробимо 10 спроб? Тоді хоча б один раз такі відмінності будуть виникати у половині випадків (0.05×10=0.5). І якщо ми у разі, коли при порівнянні за якимось ознаками, зробимо висновок, що ми щось зареєстрували насправді, ми помилимося з неприпустимо високою ймовірністю.
Доведемо сказане за допомогою експерименту. Використаємо команду set.seed(), яка визначає певну послідовність «випадкових» (насправді, псевдовипадкових) чисел, які використовує R.
set.seed(123456789) # Фіксуємо певну послідовність псевдовипадкових чисел
N <- 50 # Довжина послідовності випадкових символів, що утворюють "ознаку"
n <- 50 # Кількість зразків, що характеризовані такою "ознакою"
Randoms1 <- matrix(runif(N*n, 0, 1), nrow = N, ncol = n) # Матриця з випадковими числами
p_values1 <- rep(NA, n*(n-1)/2) # Вектор з рівнями значущості, отриманими при окремих порівняннях
nms <- rep(NA, length(p_values1)) # Позначення в цьому векторі
count <- 1 # Лічильник порівнянь
for(f in 1:(n-1)) { for(s in (f+1):n) { # Формуємо послідовність порівнянь...
test <- wilcox.test(Randoms1[, f], Randoms1[, s]) # Проводимо тести...
p_values1[count] <- test$p.value # Зберігаємо кожне p.value у вектор...
nms[count] <- paste0(f, "_vs_", s) # Створюємо підписи...
count <- count+1 }} # Переходимо до наступного порівняння
names(p_values1) <- nms # Переносимо підписи до вектору з p.value
head(p_values1); tail(p_values1) # Дивимось, що отримали
## 1_vs_2 1_vs_3 1_vs_4 1_vs_5 1_vs_6 1_vs_7
## 0.9203758 0.9587648 0.5695325 0.3259179 0.5836516 0.9972498
## 47_vs_48 47_vs_49 47_vs_50 48_vs_49 48_vs_50 49_vs_50
## 0.73291984 0.01659308 0.16064894 0.08796705 0.42589476 0.22633055
length(p_values1) # Рахуємо кількість порівнянь
## [1] 1225
length(p_values1[which(p_values1<0.05)]) # Рахуємо кількість порівнянь, які ми могли б вважати «значущими», якщо б проводили один-єдиний тест
## [1] 64
which(p_values1<0.05) # Дивимось, які саме ці порівняння
## 4_vs_18 4_vs_22 4_vs_30 4_vs_36 4_vs_42 4_vs_47 5_vs_12 5_vs_28
## 158 162 170 176 182 187 197 213
## 5_vs_44 5_vs_49 6_vs_44 8_vs_44 12_vs_18 12_vs_22 12_vs_27 12_vs_30
## 229 234 273 358 490 494 499 502
## 12_vs_36 12_vs_42 12_vs_43 12_vs_47 15_vs_18 15_vs_42 18_vs_28 18_vs_34
## 508 514 515 519 598 622 707 713
## 18_vs_37 18_vs_44 18_vs_46 18_vs_49 19_vs_28 19_vs_44 19_vs_49 22_vs_28
## 716 723 725 728 738 754 759 825
## 22_vs_44 22_vs_49 24_vs_44 26_vs_44 27_vs_28 27_vs_44 27_vs_49 28_vs_30
## 841 846 894 943 950 966 971 974
## 28_vs_33 28_vs_36 28_vs_42 28_vs_43 28_vs_47 29_vs_42 30_vs_37 30_vs_44
## 977 980 986 987 991 1007 1022 1029
## 30_vs_49 33_vs_44 34_vs_42 36_vs_44 36_vs_49 37_vs_42 38_vs_44 39_vs_44
## 1034 1083 1097 1128 1133 1139 1153 1164
## 42_vs_44 42_vs_46 42_vs_49 43_vs_44 43_vs_49 44_vs_47 44_vs_48 47_vs_49
## 1191 1193 1196 1198 1203 1207 1208 1221З 1225 порівнянь 64 виявилися такими, де отримано p<0.05!
Може, якщо ми порівнюємо два об’єкти по багатьом ознакам, ситуація буде принципово іншою? Ні. Перевіримо й це.
i <- 10 # Довжина послідовності випадкових символів, що утворюють "ознаку"
j <- 200 # Кількість "ознак", якими характеризований кожний зразок
Randoms2 <- matrix(runif(i*j*2, 0, 1), nrow = i*j, ncol = 2) # Матриця з випадковими числами
p_values2 <- rep(NA, j) # Вектор з рівнями значущості, отриманими при окремих порівняннях
for(ch in 1:j) { # Формуємо послідовність порівнянь...
test <- wilcox.test(Randoms2[((ch-1)*i+1):(ch*i), 1], Randoms2[((ch-1)*i+1):(ch*i), 2]) # Проводимо тести...
p_values2[ch] <- test$p.value } # Зберігаємо кожне p.value у вектор...
head(p_values2); tail(p_values2) # Дивимось, що отримали
## [1] 0.16549395 0.08920955 0.73936435 0.73936435 0.21756262 0.24745069
## [1] 0.4358722 0.2798610 0.8534283 0.2474507 0.5288489 0.3526814
length(p_values2) # Рахуємо кількість порівнянь
## [1] 200
length(p_values2[which(p_values2<0.05)]) # Рахуємо кількість порівнянь, які ми могли б вважати «значущими», якщо б проводили один-єдиний тест
## [1] 8
which(p_values2<0.05) # Дивимось, які саме ці порівняння
## [1] 7 20 69 76 80 93 151 160На 200 порівнянь випадкових послідовностей чисел ми отримали 8 таких, де p<0.05! Ми можемо на підставі цього результату вирішити, що саме 7-й, 20-й, 69-й тощо відтінки послідовності випадкових чисел є такими, які насправді значуще відрізняють першу послідовність від другої? Наші роздуми про те, які особливості відрізняють саме ці порівняння, будуть мати сенс? Звісно, ні.
Так що ж робити?
Використовувати поправку на множинні порівняння!
9.12 Поправки на множинні порівняння
Найпростіше рішення проблеми множинних порівнянь запропонував італійський математик Карло Еміліо Бонферроні. Ми проводимо n статистичних тестів та отримуємо n окремих p (p-levels). Якщо б ми проводили один-єдиний тест, ми б порівнювали це p з α — критичним рівнем значущості. У разі n тестів ми вираховуємо таке q (p-adjusted), яке дорівнює p×n (якщо p×n>1 ⟶ q=1), і порівнюємо q з α. Звісно, можна робити й інакше — розділити α на n, але у такому випадку розрахунків легше було б заплутатися.
У минулому пункті ми отримали вектор p_values1, що містить низку p-levels від множинного проведення тесту. Застосувати поправку Бонферроні можна за допомогою функції p.adjust(), яка отримує послідовність p-levels та перетворює її на послідовність p-adjusted.
p.adjust(p_values1, method = "bonferroni")
## 1_vs_2 1_vs_3 1_vs_4 1_vs_5 1_vs_6 1_vs_7 1_vs_8 1_vs_9
## 1 1 1 1 1 1 1 1
## 1_vs_10 1_vs_11 1_vs_12 1_vs_13 1_vs_14 1_vs_15 1_vs_16 1_vs_17
## 1 1 1 1 1 1 1 1
(...і далі усі інші результати)
Скільки порівнянь дали значущий результат?
alpha <- 0.05
length(which(p.adjust(p_values1, method = "bonferroni") < alpha))
## [1] 0Жодного! І саме так і мало бути.
Застосований нами приклад є доведеним до абсурду. Використаємо його у більш наближеному до реальних ситуацій варіанті. Використаємо приклад, який ми розглядали, обговорюючи тест Краскела-Волліса.
Можна було б провести перебір усіх пар генотипів автоматично, але для більшої зрозумілості коду переберемо усі пари вручну.
nms <- c("LL_LLR", "LL_LR", "LL_LRR", "LL_RR", "LRL_LR", "LLR_LRR", "LLR_RR", "LR_LRR", "LR_RR", "LRR_RR")
p_val_TiFm_Genotyps <- rep(NA, 10)
names(p_val_TiFm_Genotyps) <- nms
test <- wilcox.test(Ti_Fm[which(Genotyp=="LL")], Ti_Fm[which(Genotyp=="LLR")])
p_val_TiFm_Genotyps[1] <- test$p.value
test <- wilcox.test(Ti_Fm[which(Genotyp=="LL")], Ti_Fm[which(Genotyp=="LR")])
p_val_TiFm_Genotyps[2] <- test$p.value
test <- wilcox.test(Ti_Fm[which(Genotyp=="LL")], Ti_Fm[which(Genotyp=="LRR")])
p_val_TiFm_Genotyps[3] <- test$p.value
test <- wilcox.test(Ti_Fm[which(Genotyp=="LL")], Ti_Fm[which(Genotyp=="RR")])
p_val_TiFm_Genotyps[4] <- test$p.value
test <- wilcox.test(Ti_Fm[which(Genotyp=="LLR")], Ti_Fm[which(Genotyp=="LR")])
p_val_TiFm_Genotyps[5] <- test$p.value
test <- wilcox.test(Ti_Fm[which(Genotyp=="LLR")], Ti_Fm[which(Genotyp=="LRR")])
p_val_TiFm_Genotyps[6] <- test$p.value
test <- wilcox.test(Ti_Fm[which(Genotyp=="LLR")], Ti_Fm[which(Genotyp=="RR")])
p_val_TiFm_Genotyps[7] <- test$p.value
test <- wilcox.test(Ti_Fm[which(Genotyp=="LR")], Ti_Fm[which(Genotyp=="LRR")])
p_val_TiFm_Genotyps[8] <- test$p.value
test <- wilcox.test(Ti_Fm[which(Genotyp=="LR")], Ti_Fm[which(Genotyp=="RR")])
p_val_TiFm_Genotyps[9] <- test$p.value
test <- wilcox.test(Ti_Fm[which(Genotyp=="LRR")], Ti_Fm[which(Genotyp=="RR")])
p_val_TiFm_Genotyps[10] <- test$p.value
p_val_TiFm_Genotyps
## LL_LLR LL_LR LL_LRR LL_RR LRL_LR LLR_LRR
## 0.2211538462 0.0142758858 0.0193744164 0.0020639835 0.0442284740 0.0474483844
## LLR_RR LR_LRR LR_RR LRR_RR
## 0.0001215955 0.6500355464 0.0241243774 0.0682643095Що б у нас вийшло, якби ми не використовували поправку Бонферроні?
alpha <- 0.05
p_val_TiFm_Genotyps < alpha
## LL_LLR LL_LR LL_LRR LL_RR LRL_LR LLR_LRR LLR_RR LR_LRR LR_RR LRR_RR
## FALSE TRUE TRUE TRUE TRUE TRUE TRUE FALSE TRUE FALSE
length(which(p_val_TiFm_Genotyps < alpha))
## [1] 7Серед невідкорегованих значень p сім є меншими за α. А серед корегованих?
p.adjust(p_val_TiFm_Genotyps, method = "bonferroni")
## LL_LLR LL_LR LL_LRR LL_RR LRL_LR LLR_LRR
## 1.000000000 0.142758858 0.193744164 0.020639835 0.442284740 0.474483844
## LLR_RR LR_LRR LR_RR LRR_RR
## 0.001215955 1.000000000 0.241243774 0.682643095
p.adjust(p_val_TiFm_Genotyps, method = "bonferroni") < alpha
## LL_LLR LL_LR LL_LRR LL_RR LRL_LR LLR_LRR LLR_RR LR_LRR LR_RR LRR_RR
## FALSE FALSE FALSE TRUE FALSE FALSE TRUE FALSE FALSE FALSE
length(which(p.adjust(p_val_TiFm_Genotyps, method = "bonferroni") < alpha))
## [1] 2Лишилося тільки два — зате відносно цих двох порівнянь ми можемо вважати, що, скоріше за все, ми не помилимося, вважаючи різницю між LL та RR, а також між LLR та RR доведеною.
Втім, прийнято вважати, що метод Бонферроні небажано використовувати у разі кількості порівнянь, більших за 7 або 8. А якщо порівнянь більше? Використовувати більш потужні (і більш складні) методи, наприклад, метод Хольма-Бонферроні (чи метод Бонферроні з поправкою Хольма). Втім, у нашому випадку більш потужний метод не приводить до зміни отриманого результату.
p.adjust(p_val_TiFm_Genotyps, method = "holm")
## LL_LLR LL_LR LL_LRR LL_RR LRL_LR LLR_LRR
## 0.442307692 0.114207086 0.135620915 0.018575851 0.221142370 0.221142370
## LLR_RR LR_LRR LR_RR LRR_RR
## 0.001215955 0.650035546 0.144746265 0.221142370
p.adjust(p_val_TiFm_Genotyps, method = "holm") < alpha
## LL_LLR LL_LR LL_LRR LL_RR LRL_LR LLR_LRR LLR_RR LR_LRR LR_RR LRR_RR
## FALSE FALSE FALSE TRUE FALSE FALSE TRUE FALSE FALSE FALSE
length(which(p.adjust(p_val_TiFm_Genotyps, method = "holm") < alpha))
## [1] 2А якщо б нас не цікавили 9 з 10 пар генотипів, які ми порівнювали за відношенням гомілки до стегна, а з самого початку ми встановлювали б одну-єдину річ: чи відрізняються за цім відношенням особини Pelophylax lessonae від диплоїдних особин Pelophylax esculentus? Ми б провели один тест і отримали б значущий результат!
wilcox.test(Ti_Fm[which(Genotyp=="LL")], Ti_Fm[which(Genotyp=="LR")])
##
## Wilcoxon rank sum exact test
##
## data: Ti_Fm[which(Genotyp == "LL")] and Ti_Fm[which(Genotyp == "LR")]
## W = 9, p-value = 0.01428
## alternative hypothesis: true location shift is not equal to 0