 |
||||
|
← |
Д.А. Шабанов, М.А.Кравченко. Статистический анализ данных в зоологии и экологии |
→ |
||
|
Тема 8. Кластерный анализ |
||||
|
Биостатистика-11 |
Биостатистика-13 |
|||
8.1. Сущность кластерного анализа
Кластерным анализом называются разнообразные формализованные процедуры построения классификаций объектов. Лидирующей наукой в развитии кластерного анализа была биология. Предмет кластерного анализа (от англ. «cluster» — гроздь, пучок, группа) был сформулирован в 1939 г. психологом Робертом Трионом. Классиками кластерного анализа являются американские систематики Роберт Сокэл и Питер Снит. Одно из важнейших их достижений в этой области — книга «Начала численной таксономии», выпущенная в 1963 году. В соответствии с основной идеей авторов, классификация должна строится не на смешении плохо формализованных суждений о сходстве и родстве объектов, а на результатах формализованной обработки результатов математического вычисления сходств/отличий классифицируемых объектов. Для выполнения этой задачи нужны были соответствующие процедуры, разработкой которых и занялись авторы.
Основные этапы кластерного анализа таковы:
1. выбор сравнимых друг с другом объектов;
2. выбор множества признаков, по которому будет проводиться сравнение, и описание объектов по этим признакам;
3. вычисление меры сходства между объектами (или меры различия объектов) в соответствии с избранной метрикой;
4. группировка объектов в кластеры с помощью той или иной процедуры объединения;
5. проверка применимости полученного кластерного решения.
Итак, важнейшими характеристиками процедуры кластеризации является выбор метрики (в разных ситуациях используется значительное количество разных метрик) и выбор процедуры объединения (и в этом случае для выбора доступно значительное количество различных вариантов). Для разных ситуаций в большей степени подходят одни или другие метрики и процедуры объединения, но в определенной степени выбор между ними является вопросом вкуса и традиции. Как более подробно объясняется в статье Кластеры, клады и химера объективности, надежда на то, что кластерный анализ приведет к построению классификации, никак не зависимой от произвола исследователя, оказывается недостижимой. Из пяти перечисленных этапов исследования с использованием кластерного анализа только этап 4 не связан с принятием более-менее произвольного решения, влияющего на конечный результат. И выбор объектов, и выбор признаков, и выбор метрики вместе с процедурой объединения существенно влияют на конечный результат. Этот выбор может зависит от многих обстоятельств, а том числе — от явных и неявных предпочтений и ожиданий исследования. Увы, указанное обстоятельство влияет не только на результат кластерного анализа. Со сходными проблемами сталкиваются все "объективные" методы, включая все методы кладистики.
Существует ли единственно правильное решение, которое надо найти, выбирая совокупность объектов, набор признаков, тип метрики и процедуру объединения? Нет. Чтобы доказать это, приведем фрагмент статьи, ссылка на которую дана в предыдущем абзаце.
"На самом деле, мы не всегда можем даже твердо ответить на вопрос, какие объекты более похожи друг на друга, а какие отличаются сильнее. Увы, для выбора метрики сходств и различий между классифицируемыми объектами общепринятых (а тем более «объективных») критериев попросту нет.
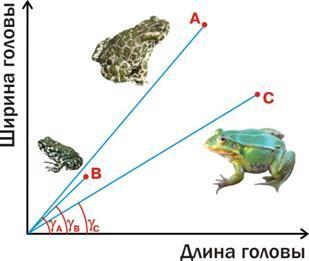
На какой объект более похож объект А: на B или на C? Если использовать в качестве метрики сходства расстояние, то на C: |AC|<|AB|. А если полагаться на корреляцию между показанными на рисунке признаками (которую можно описать как угол между вектором, идущим к объекту из начала координат, и осью абсцисс), то на B: 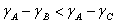 . А как правильно? А единственно правильного ответа нет. С одной стороны, взрослая жаба более похожа на взрослую лягушку (обе взрослые), с другой — на молодую жабу (обе жабы)! Правильность ответа зависит от того, что мы считаем более важным".
. А как правильно? А единственно правильного ответа нет. С одной стороны, взрослая жаба более похожа на взрослую лягушку (обе взрослые), с другой — на молодую жабу (обе жабы)! Правильность ответа зависит от того, что мы считаем более важным".
Кластерный анализ нашел широчайшее применение в современной науке. К сожалению, в значительной части тех случаев, когда его употребляют, лучше было бы использовать иные методы. В любом случае, стециалистам-биологом надо отчетливо понимать основную логику кластерного анализа, и только в этом случае они смогут применять его в тех случаях, где он адекватен, и не применять тогда, когда оптимальным является выбор иного метода.
8.2. Пример выполнения кластерного анализа "на пальцах"
Чтобы пояснить типичную логику кластерного анализа, рассмотрим его наглядный пример. Рассмотрим совокупность из 6 объектов (обозначенных буквами), охарактеризованных по 6 признакам самого простого типа: альтернативных, принимающих одно из двух значений: характерен (+) и нехарактерен (—). Описание объектов по принятым признакам называется "прямоугольной" матрицей. В нашем случае речь идет о матрице 6×6, т.е. ее можно считать вполне "квадратной", но в общем случае количество объектов в анализе может не быть равно количеству признаков, и "прямоугольная" матрица может иметь разное количество строк и столбцов. Итак, зададим "прямоугольную" матрицу (матрицу объекты/признаки):
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
A |
— |
+ |
+ |
— |
+ |
+ |
|
B |
— |
+ |
— |
— |
— |
+ |
|
C |
— |
+ |
— |
+ |
+ |
— |
|
D |
+ |
— |
+ |
— |
— |
+ |
|
E |
+ |
— |
— |
+ |
— |
+ |
|
F |
+ |
+ |
— |
— |
— |
+ |
Выбор объектов и описание их по определенному набору признаков соответствуют двум первым этапам кластерного анализа. Следующий этап — построение матрицы сходств или различий ("квадратной" матрицы, матрицы объекты/объекты). Для этого нам надо выбрать метрику. Поскольку наш пример носит условный характер, имеет смысл выбрать самую простую метрику. Как проще всего определить расстояние между объектами A и B? Посчитать количество отличий между ними. Как вы можете увидеть, объекты A и B отличаются по признакам 3 и 5, итого, расстояние между этими двумя объектами соответствует двум единицам.
Пользуясь этой метрикой, построим "квадратную" матрицу ( матрицу объекты/ объекты). Как легко убедиться, такая матрица состоит из двух симметричных половин, и заполнять можно только одну из таких половин:
|
|
A |
B |
C |
D |
E |
F |
|
A |
— |
2 |
3 |
3 |
5 |
3 |
|
B |
|
— |
3 |
3 |
3 |
1 |
|
C |
|
|
— |
6 |
4 |
4 |
|
D |
|
|
|
— |
2 |
2 |
|
E |
|
|
|
|
— |
2 |
|
F |
|
|
|
|
|
— |
В данном случае мы построили матрицу различий. Матрица сходства выглядела бы подобным образом, только на каждой позиции стояла бы величина, равная разности между максимальной дистанции (6 единиц) и различию между объектами. Для пары A и B, естественно, сходство составило бы 4 единицы.
Какие два объекта ближе всего друг к другу? B и F, они отличаются только по одному признаку. Суть кластерного анализа — в объединении подобных объектов в кластер. Объединяем объекты B и F в кластер (BF). Покажем это на схеме. Как вы видите, объекты объединены на том уровне, который соответствует дистанции между ними.
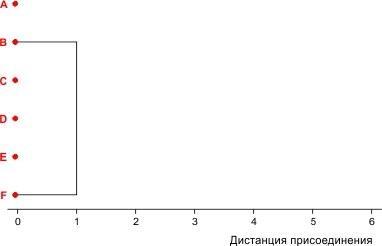
Рис. 8.2.1. Первый шаг кластеризации условного набора из 6 объектов
Теперь у нас не шесть объектов, а пять. Перестраиваем "квадратную" матрицу. Для этого нам потребуется определить, чему равно расстояние от каждого объекта до кластера. Растояние от A до B составляло 2 единицы, а от A до F — 3 единицы. Чему равно расстояние от A до (BF)? Правильного ответа тут нет. Вот, посмотрите, как расположены друг относительно друга эти три объекта.

Рис. 8.2.2. Взаимное расположение трех объектов
Может быть, расстояние от объекта до группы — это расстояние от объекта до ближайшего к нему объекта в составе группы, т.е., │A(BF)│=│AB│? Эта логика соответствует присоединению по максимальному сходству.
А может быть, расстояние от объекта до группы — это расстояние от объекта до наиболее удаленного от него объекта в составе группы, т.е., │A(BF)│=│AF│? Эта логика соответствует присоединению по минимальному сходству.
Можно также считать, что расстояние от объекта до группы — это среднее арифметическое расстояний от этого объекта до каждого из объектов в составе группы, т.е., │A(BF)│=(│AB│+│AF│)/2. Это решение называется присоединением по среднему сходству.
Правильным являются все эти три решения и еще значительное количество иных, не охарактеризованных здесь решений. Наша задача состоит в том, чтобы выбрать решение, более подходящее для той категории, к которой относятся наши данные. Присоединение по максимальному сходству приводит, в конечном счете, к длинным, "лентовидным" кластерам. По минимальному — к дроблению групп. Выбирая между тремя охарактеризованными вариантами, в биологии чаще используют присоединение по среднему сходству. Воспользуемся им и мы. В таком случае после первого шага кластеризации "квадратная" матрица будет выглядеть так.
|
|
A |
(BF) |
C |
D |
E |
|
A |
— |
2.5 |
3 |
3 |
5 |
|
(BF) |
|
— |
3.5 |
2.5 |
2.5 |
|
C |
|
|
— |
6 |
4 |
|
D |
|
|
|
— |
2 |
|
E |
|
|
|
|
— |
Теперь самой близкой парой объектов являются D и E. Объединим и их тоже.
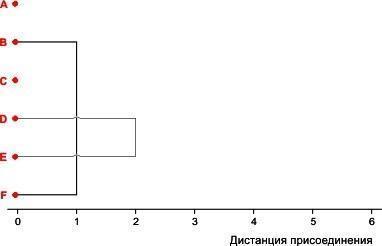
Рис. 8.2.3. Второй шаг кластеризации условного набора из 6 объектов
Перестроим "квадратную" матрицу для четырех объектов.
|
|
A |
(BF) |
C |
(DE) |
|
A |
— |
2,5 |
3 |
4 |
|
(BF) |
|
— |
3,5 |
2,5 |
|
C |
|
|
— |
5 |
|
(DE) |
|
|
|
— |
Мы видим, что тут есть две возможности для объединения на уровне 2,5: присоединение A к (BF) и присоединение (BF) к (DE). Какую из них выбрать?
У нас есть различные варианты, как делать такой выбор. Его можно сделать случайно. Можно принять какое-то формальное правило, позволяющее сделать выбор. А можно посмотреть, какое из решений даст лучший вариант кластеризации. Воспользуемся последним вариантом. Вначале реализуем первую возможность.
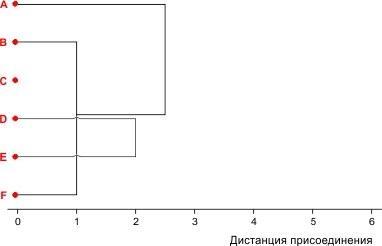
Рис. 8.2.4. Первый вариант третьего шага кластеризации условного набора из 6 объектов
Выбрав этот вариант, мы должны были бы построить такую "квадратную" матрицу 3×3.
|
|
(ABF) |
C |
(DE) |
|
(ABF) |
— |
3,25 |
3,25 |
|
C |
|
— |
5 |
|
(DE) |
|
|
— |
Если бы мы выбрали второй вариант третьего шага, у нас получилась бы следующая картина.
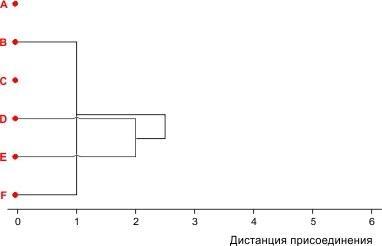
Рис. 8.2.5. Второй вариант третьего шага кластеризации условного набора из 6 объектов
Ему соответствует такая матрица 3×3:
|
|
A |
C |
(BFDE) |
|
A |
— |
3 |
3,25 |
|
C |
|
— |
4 |
|
(BFDE) |
|
|
— |
Получившиеся матрицы 3×3 можно сравнить, и убедиться, что более компактная группировка объектов достигается во втором варианте. При построении классификации объектов с помощью кластерного анализа мы должны стремиться выделить группы, которые объединяют сходные объекты. Чем выше сходство объектов в группах, тем лучше такая классификация. Поэтому мы выбираем второй вариант третьего шага кластеризации. Мы, конечно, могли сделать следующие шаги (и разделить первый вариант еще на два подварианта), но, в конце концов, убедились бы, что лучшим вариантом третьего шага кластеризации является именно тот, который показан на рис. 8.5. Останавливаемся на нем.
В таком случае, следующим шагом является объединение объектов A и C, показанный на рис. 8.6.
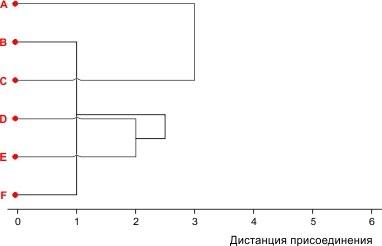
Рис. 8.2.6. Четвертый шаг кластеризации
Строим матрицу 2×2:
|
|
(AC) |
(BFDE) |
|
(AC) |
— |
3,625 |
|
(BFDE) |
|
— |
Теперь выбирать уже нечего. Объединим два оставшихся кластера на требуемом уровне. В соответствии с принятой стилистикой построения кластерных "деревьев" добавим еще "ствол", который тянется до уровня максимально возможной при данном наборе признаков дистанции между объектами.
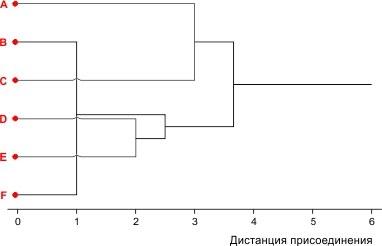
Рис. 8.2.7. Пятый и последний шаг кластеризации
Получившаяся картина является древовидным графом (совокупностью вершин и связей между ними). Этот граф построен так, что образующие его линии пересекают друг друга (мы показали эти пересечения "мостиками"). Без изменения характера связи между объектами граф можно перестроить так, чтобы в нем не было никаких пересечений. Эти и сделано на рис. 8.2.8.
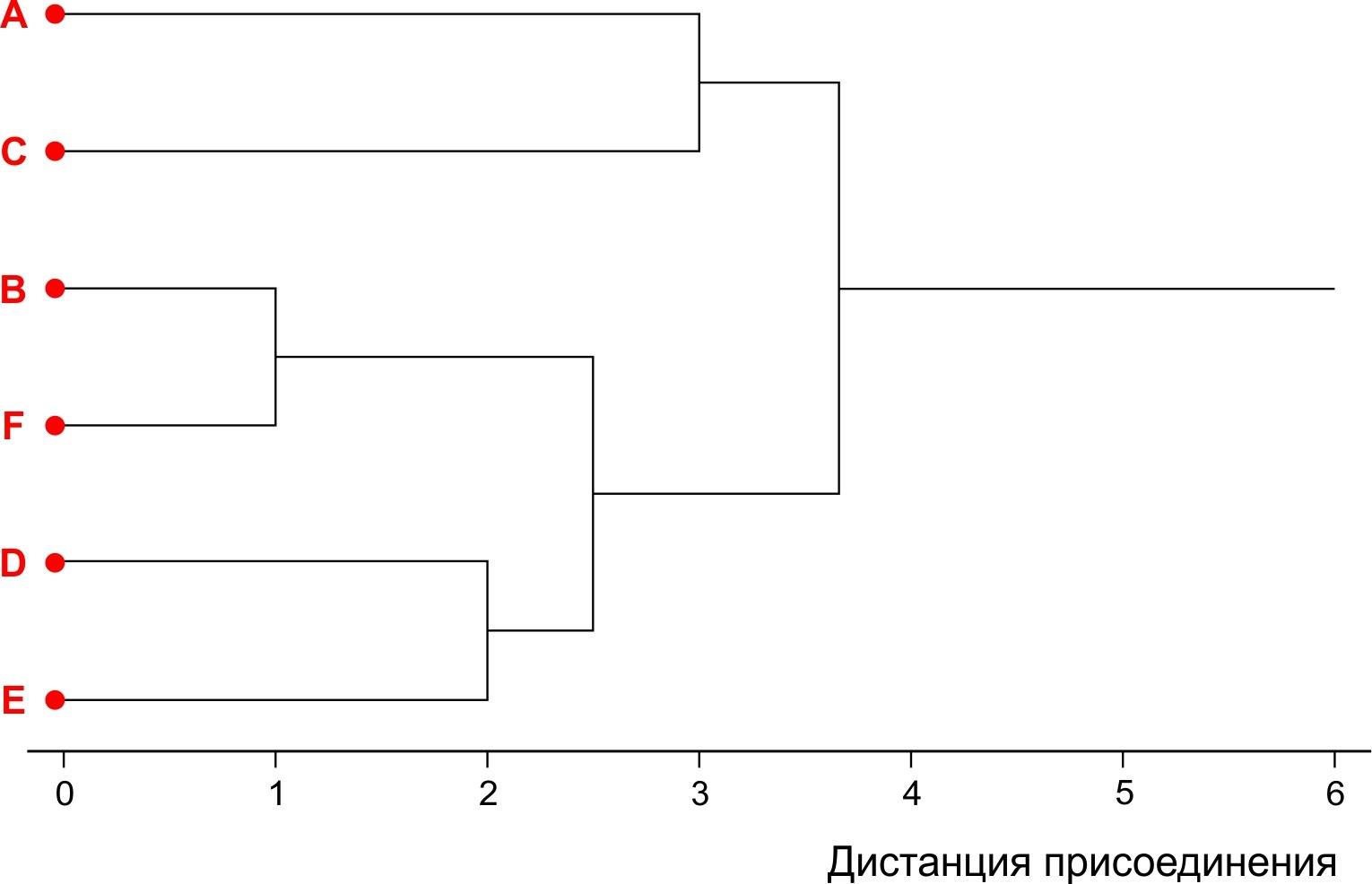
Рис. 8.2.8. Окончательный вид древовидного графа, полученного в результате кластеризации
Кластерный анализ нашего условного примера закончен. Нам осталось только понять, что же мы получили.
8.3. Принципиальные ограничения и недостатки кластерного анализа
Как интерпретировать граф, показанный на рис. 8.2.8? Однозначного ответа нет. Чтобы ответить на этот вопрос, надо понимать, какие данные и для какой цели мы кластеризовали. "На поверхности" лежит вывод, что мы зарегистрировали, что исходная совокупность из 6 объектов состоит из трех пар. Глядя на получившийся график, в этом трудно усомниться. Однако справедлив ли этот вывод?
Вернитесь к самой первой "квадратной" матрице 6×6 и убедитесь: объект E находился на расстоянии в две единицы и от объекта D, и от объекта F. Сходство E и D на итоговом "дереве" отражено, а вот то, что объект E был столь же близок к объекту F — потерялось без следа! Как это объяснить?
В том результате кластеризации, который показан на рис. 8.2.8, полностью отсутствует информация о дистанции │EF│, там есть только информация о дистанциях │DE│ и │(BF)(DE)│!
Каждой "прямоугольной" матрице в случае, когда выбрана определенная метрика и способ присоединения, соответствует одна-единственная "квадратная" матрица. Однако каждой "квадратной" матрице может соответствовать много "прямоугольных" матриц. После каждого шага анализа каждой предшествовавшей "квадратной" матрице соответствует следующая, но, исходя из следующей, мы не смогли бы восстановить предшествовавшую. Это означает, что при каждом шаге кластерного анализа необратимо теряется некая часть информации о разнообразии исходного набора объектов.
Указанное обстоятельство является одним из серьезных недостатков кластерного анализа.
Еще один из коварных недостатков кластерного анализа упомянут в статье Ложь, наглая ложь и…, в разделе "Непонимание сути метода".