Creation of Worlds — 10. Приклади різноманітних моделей, їх задум і дизайн

10. Приклади різноманітних моделей, їх задум і дизайн

10.1. Підбірка моделей для знайомства з варіантами їх побудови

Можна не сумніватися, що для того, щоб з успіхом використовувати імітаційне моделювання в своїй роботі, біологу потрібно вміти не тільки використовувати найпростіші інструменти для побудови моделей. Він повинен бачити ситуації, в яких йому може допомогти моделювання, вміти ставити завдання, яку повинна вирішувати модель, а також розробляти дизайн моделі — набір вхідних параметрів, обчислюваних величин, зв'язків між ними, і, в кінцевому рахунку, набір вихідних параметрів моделі.

Як навчиться цим умінням? Аналізуючи чужі моделі і створюючи власні.

Автор даного курсу пропонує розглянути декілька моделей, які йому доводилося розробляти для вирішення різних завдань. Далеко не в усіх відношеннях ці моделі є взірцевими (скоріше — навпаки); тим не менш, студенти можуть отримати корисний для себе досвід не тільки аналізуючи гідності наявних моделей, але навіть розглядаючи їх недоліки. Моделі, приклади яких тут наведені, робилися для ілюстрації тих чи інших положень, що обговорювалися в колонках (статтях, що відображають авторську точку зору) в журналі "Компьютерра". Щоб розібратися в структуру й особливості моделей, треба прочитати самі колонки (а також, при необхідності, джерела, на які ці колонки посилаються) і побачити, куди "вписані" розглянуті моделі.

47. Когда отбор становится неэффективным? Модель з цієї колонки можна скачати тут.

50. Альтруизм и парадокс Симпсона. Модель (громіздку, "некрасиву") з цієї колонки можна скачати тут.

51. Подпорки альтруизма. З цієї колонки модель розміщена тут.

137. Обсуждение перехода от гермафродитизма к раздельнополости как пример неклассического развития естественнонаучной гипотезы. Модель до цієї колонки описана далі, а сама вона наявна у варианті для Excel-2013 та у варианті для Excel-2003.

138. О природе мужского и женского, или от конъюгации к оогамии. Ось варианти модели для Excel-2013 та для Excel-2003.

Задача про хлопчиків та дівчат. Ця задача викликала суперечки. Простой спосіб отримати однозначну відповідь — побудувати модель. 

 

10.2. Модель динаміки епідемії

Нижче наведено опис створення нескладної моделі, що описує поширення епідемії. Цю модель можна завантажити з сайту або створити самостійно згідно з описом (останнє — краще).

Модель розглядає чотири стани особин: вразливий ( код 1), хворий (2), імунний (3), померлий (4). Для моделювання слід задати ймовірності переходів між цими станами: зараження імунного при наявності поруч хворого (1→2), а також одужання хворого і його переходу у стан імунного (1→3). Ймовірність загибелі хворого — одиниця мінус ймовірність його одужання.

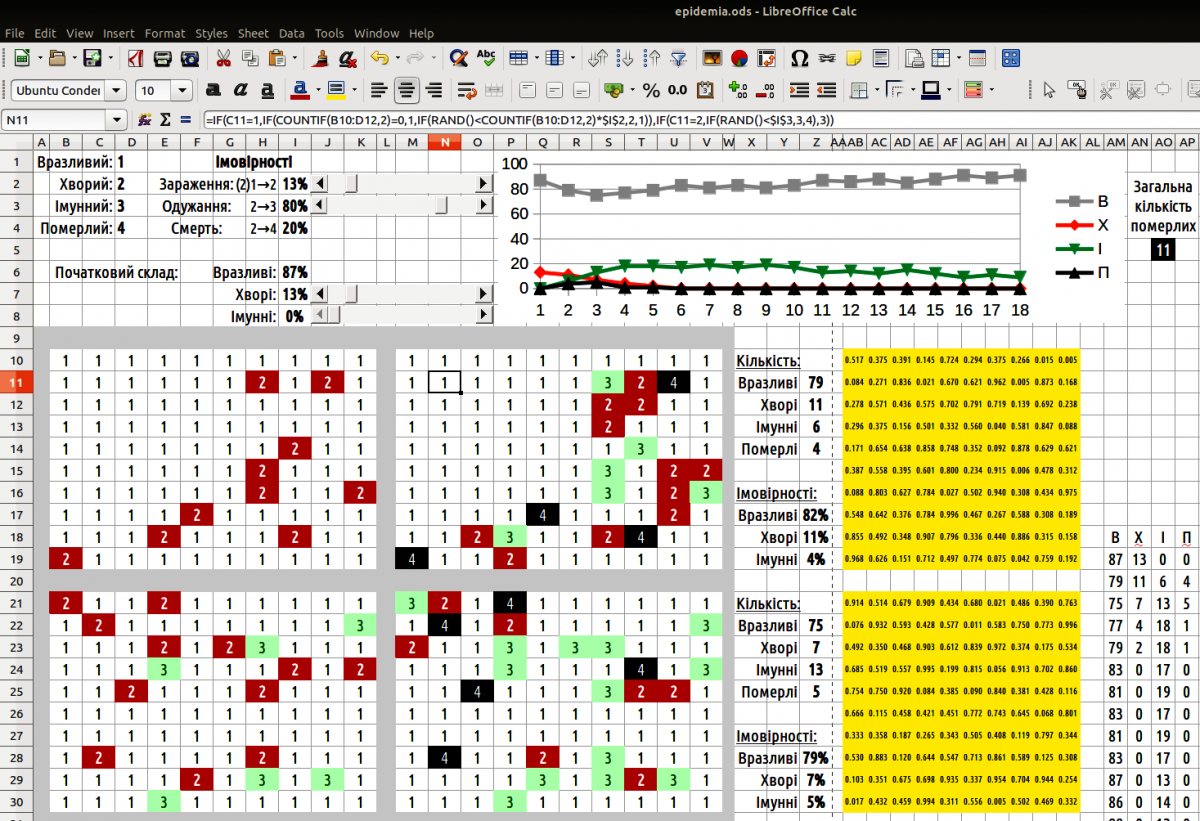
Рис. 10.1.1. Окно моделі epidemia

Щоб керувати змінами цих навчальних параметрів можна застосувати смугу прокрутки. Щоб вставити смугу, пройдіть по шляху «Перегляд / Панелі інструментів» і оберіть панель «Елементи керування». На аркуші LO Calc з'явиться ця панель. Перейдіть в режим розробки за допомогою кнопки, на якій написано «ОК»: «Режим розробки». Вам стануть доступні елементи управління, серед яких можна вибрати смугу прокрутки. Вибравши її, окресліть якийсь простір на аркуші; LO Calc вставить туди цей елемент управління. Залежно від того, який простір ви окреслите для цього елементу, він буде горизонтальним або вертикальним.

Щоб налаштувати смугу прокрутки, виділіть її, залишаючись в режимі розробки. Стане активною кнопка «Елемент керування», на якій зображені перекреслені інструменти. Натиснувши її, ви потрапите в діалог «Властивості: Смуга прокрутки». На першій вкладці, «Загальні», можна налаштувати властивості смуги, в число яких входять розміри, положення, мінімальне і максимальне значення, що задаються за допомогою цієї смуги, крок зміни, її розміри тощо. На другій вкладці, «Дані», слід вказати ту комірку, значення в якій буде змінюватися за допомогою цієї смуги прокрутки. Після того, як властивості елементу керування налаштовані, вікно діалогу можна просто закрити: зміни будуть збережені. Зверніть увагу: смуга прокрутки запрацює лише тоді, коли ви вийдете з режиму розробки! Щоб змінити розташування смуги або її інші властивості, треба буде знову входити у режим розробки.

Один зі способів використання смуги прокрутки такий. Смуга керує значенням, що знаходиться у певній комірці (можна — у комірці, що розташована під самою смугою). Значення цієї комірки змінюється від 1 до 100. У комірці, де розраховується значення початкового параметру, стоїть формула, що ділить значення комірки, якою керує смуга прокрутки, на 100. Це значення можна показувати у процентах. Такий ускладнений шлях пов’язаний з тим, що за допомогою смуги прокрутки можна задавати лише цілі значення, а початкові параметри (ймовірності) мають бути виражені частками одиниці.

Крім того, до числа початкових параметрів належить початковий склад популяції. Його також можна задавати за допомогою смуг прокрутки. Наприклад, можна визначити частку хворих та частку імунних; усі інші особини — це вразливі.

Найпростіший варіант побудови моделі такий. На певному просторі (у прикладі, що надається, це — прямокутник 10 на 10, але можливий і будь-який інший варіант) слід випадково розташувати особин відповідно до розподілу, що заданий початковими параметрами. Для кожної комірки на цьому полі слід визначити, яка особина її займає. Для таких задач слід використовувати порівняння випадкового числа (від 0 до 1) з розподілом одиниці. Якщо б ми розглядали 2 стани комірок (наприклад, білі та чорні), ми могли б вираховувати випадкове число у самій формулі (якщо випадкове число менша за ймовірність появи білої клітини — комірка біла, а якщо воно вище — чорна). Ми використовуємо розподіл з трьома станами; в одній формулі те ж саме випадкове число, що розраховується в ній самій, неможливо порівнювати водночас з двома різними числами. Тому десь на листі Calc слід розмістити поле випадкових чисел (на демонстраційній моделі це поле позначене жовтим кольором). У кожній комірці цього поля стоїть формула =RAND().

Тепер в полі початкового розподілу можна визначити, які особини займають кожну комірку. Для цього використано формулу =IF(випадкове_число<$частка_вразливих;1;IF(випадкове_число<($частка_вразливих+$частка_хворих);2;3)). Кожна комірка поля початкових значень посилається на своє випадкове число; значення часток вразливих та хворих, що задана початковими параметрами, однакова для усіх комірок на цьому полі. Наведена формула спочатку порівнює випадкове число з часткою (ймовірністю) вразливих; якщо воно менше за таку ймовірність, у комірці з’являється вразлива особина. Якщо випадкове число більше за ймовірність появи вразливої особини, воно порівнюється з сумою ймовірностей появи вразливих та хворих особин. Менша — особина буде хворою; більша — імунною. Такі формули дозволяють зайняти потрібну площу випадково розташованими особинами, ймовірність появи яких задана початковими параметрами.

Початковий розподіл слід змінити. Вразливі особини, що розташовані поруч з хворими, можуть захворіти. Хворі особини можуть одужати або вмерти. Щоб показати ці зміни нам потрібний ще одне поле (ще один прямокутник такого же розміру, як прямокутник з початковим розподілом та прямокутний з випадковими числами). Кожна комірка тут містить достатньо складну формулу.

=IF(комірка_початкового_розподілу=1;IF(COUNTIF(сусідні_комірки;2)=0;1;IF(RAND()<COUNTIF(сусідні_комірки;2)*$ймовірність_захворіти;2;1));IF(комірка_початкового_розподілу=2;IF(RAND()<$ймовірність_одужати;3;4);3)).

Щоб визначити, скільки хворих межує з вразливою особиною, слід виділити групу 3 на 3, в якій порахувати кількість хворих (двійок). Так, якщо нас цікавить, скільки двійок межує з коміркою C11, можна використати формулу COUNTIF(B10:D12;2). Сама комірка C11 також потрапляє у цю групу, але це не впливає на розрахунок, оскільки в ній одиниця, а не двійка. Ймовірність захворіти визначає добуток кількості хворих сусідів на ймовірність заразитися від хворого сусіда. Щоб визначити, чи захворіє особина, яка нас цікавить, випадкове число порівнюється з цим добутком; якщо випадкове число менше задобуток, особина захворіє. Слід врахувати, що добуток може бути більшим за одиницю (наприклад, вразлива особина має три хворих сусіди; ймовірність заразитися від кожного з них дорівнює 0,5, сумарно — більше за одиницю); тоді випадкове число завжди буде меншим добутку, і особина захворіє з ймовірністю 1.

Якщо в комірці, що нас цікавить, розташована хвора особина, вона може одужати або померти. В цьому випадку її долю також визначає порівняння випадкового числа з ймовірностями, що задані в початкових параметрах. Якщо ж в комірці початкового розподілу була не вразлива і не хвора особина, там була імунна особина. Така сама особина в ній й залишиться.

Тепер можна підрахувати, скільки яких особин у зміненому розподілі. Для цього можна використати формули =COUNTIF(діапазон;1). Діапазон — це поле зі зміненим розподілом. Наведена формула розраховує кількість вразливих. Зрозуміло, що для того, щоб показувати кількість хворих, потрібна формула =COUNTIF(діапазон;2).

На підставі кількості вразливих, хворих та імунних слід розрахувати ймовірності появи таких особин у наступному розподілі. Припустимо, що на тому місці, де були померлі особини, з’являться (з характерними ймовірностями) нові особини. Тоді ймовірність появи вразливих особин можна розрахувати за формулою =кількість_вразливих/(кількість_вразливих+кількість_хворих+кількість_імунних).

Тепер слід побудувати початковий розподіл другого циклу роботи моделі. Він будується так само, як попередній початковий розподіл, з тією різницею, що використовуються не початкові ймовірності, а ймовірності, розраховані після першого циклу роботи моделі. Природно, тут буде потрібне нове поле з випадковими числами. Втім, можна поекспериментувати і з варіантом побудови моделі, де на другому циклі (і наступних циклах) розподіл буде визначатися полем випадкових чисел першого циклу.

Щоб побудувати змінений розподіл другого циклу можна скопіювати відповідні комірки першого циклу.

Перед тим, як копіювати другий цикл до третього циклу, слід убрати абсолютну адресацію (позначки $) з формул. Якщо це не зробити, початкове поле третього циклу буде будуватися у відповідності до розрахунку ймовірностей появи різних особин наприкінці першого, а не другого циклу.

Щоб розподіли особин можна було оцінювати з першого погляду, можна використати умовне форматування. Виділить первинні та змінені розподіли. Пройдіть шляхом «Формат / Умовне форматування / Умова». Для кожного можливого значення оберіть тій чи інший стиль. Розподіл стане більш наочним...

Щоб побудувати графік, виведіть у одну групу кількість вразливих, хворих, імунних та померлих особин на кожному циклі. Пересуньте ці групи так, щоб вони розташувалися одна під одною. Побудуйте за цими даними графік.

 

10.3. Перехід від гермафродитизму до роздільностатевості

Подробное описание модели, иллюстрирующий процессы, описанные в колонке о переходе от гермафродитизма к раздельнополости. Модель построена в Excel-2013. Ее можно скачать по этой ссылке, а по этой — вариант для Excel-2003 (работоспособность второго варианта не проверялась!).

Модель представляет из себя лист Excel, на котором размещены блок для ввода значений начальных параметров, блок вычислений (построенных на разностных уравнениях) и блок демонстрации результатов (график). Блоки размещены на листе таким образом, чтобы все, что нужно для экспериментирования с моделью, размещалось на начальном экране.

Внешний вид начального экрана модели таков.

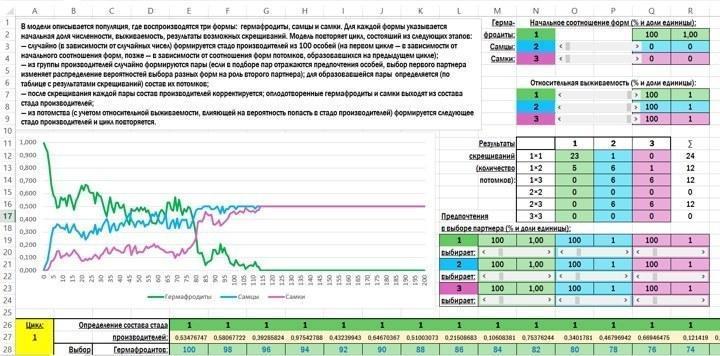
Вот то описание работы модели, которое включено в нее саму:

В модели описывается популяция, где воспроизводятся три формы:  гермафродиты, самцы и самки. Для каждой формы указывается начальная доля численности, выживаемость, результаты возможных скрещиваний. Модель повторяет цикл, состояший из следующих этапов:
— случайно (в зависимости от случайных чисел) формируется стадо производителей из 100 особей (на первом цикле — в зависимости от начального соотношения форм, позже — в зависимости от соотношения форм потомков, образовавшихся на предыдущем цикле);
— из группы производителей случайно формируются пары (если в подборе пар отражаются предпочтения особей, выбор первого партнера изменяет распределение вероятностей выбора разных форм на роль второго партнера); для образовавшейся пары  определяется (по таблице с результатами скрещиваний) состав их потомков;
— после скрещивания каждой пары состав производителей корректируется; оплодотворенные гермафродиты и самки выходят из состава стада производителей;
— из потомства (с учетом относительной выживаемости, влияющей на вероятность попасть в стадо производителей) формируется следующее стадо производителей и цикл повторяется.

В блоке для определения начальных параметров используются элементы управления, называемые в Excel полосами прокрутки.

В работе модели используется кодировка: гермафродиты обозначаются цифрой 1, самцы — 2, самки — 3. Ячейки, где могут находится эти символы, подсвечиваются разным образом в зависимости от того, какой символ в них находится.

При вводе в модель начальной численности (начального соотношения форм) с помощью полос прокрутки устанавливается процентная доля самцов и самкок (в диапазоне от 0% до 50%); в зависимости от этих значений определяется численность гермафродитов.

При определении относительной выживаемости с помощью полос прокрутки для всех трех форм устанавливается выживаемость от 0% до 100%. Абсолютная выживаемость в модели не рассматривается. Предположим, из 1000 гермафродитов выживает 8, из 1000 самцов — 10, из 1000 самок — 5. В таком случае относительная выживаемость самцов (самого успешного пола) составляет 100%, гермафродитов — 80%, а самок — 50%.

В таблице, где задаются результаты скрещиваний, на пересечении строк и столбцов, соответствующих двум партнерам, указывается количество их потомков.

Предпочтения при выборе партнеров задаются с помощью полос прокрутки. Все значения изменяются от 0% до 500%. Значение 100% соответствует равной вероятности выбора, более низкие — снижению такой вероятности, более высокие — ее повышению.

Фрагмент рабочей зоны файла с пояснениями, что вычисляется в ее ячейках, приведен на рисунке.

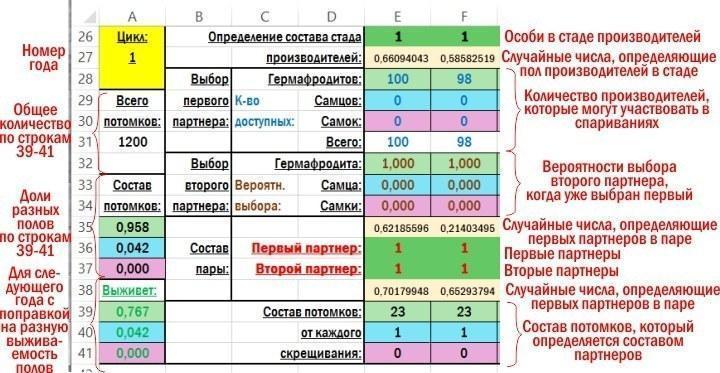
Вначале вычисляется состав стада производителей, которые для первого года (цикла вычисления) располагаются в строке 26. Сразу вычисляется все 100 особей. Потом вычисления идут по столбцам внутри группы строк, соответствующих году. Охарактеризовать использоваемые вычисления проще всего, перечислив эти ячейки по порядку, используя адреса строк. Скопированные из ячеек модели формулы подсвечены желтым фоном.

F26 — =ЕСЛИ(F27<$R$2;1;ЕСЛИ(F27<($R$2+$R$3);2;3)) — формула, определяющая пол особи в составе нерестового стада, в зависимости от случайного числа, находящегося в ячейке F27. $R$2 и $R$2 — адреса ячеек, в которых указаны доли представителей разных полов в популяции. При аналогичных вычислениях в годы, начиная со второго, здесь используется соотношение полов, полученное по результатам предыдущего года (A39, A40 и A41 для второго года).

F27 — =СЛЧИС() — генерируемое программой случайное число, находящееся в пределах от 0 до 1; используется для определения пола одной особи из стада производителей (ячейки F26).

F28 — =E28-(ЕСЛИ(E36=1;ЕСЛИ(E37=1;2;ЕСЛИ(E37=2;1;0));0)+ЕСЛИ(E37=1;ЕСЛИ(E36=2;1;0);0)) — вычисление количества гермафродитов в составе стада производителей, которые могут участвовать в спариваниях. Оно производятся на основании значения ячейки E28 (где определялось общее количество гермафродитов в составе стада до начала образования пар) и пола особей в ячейках E36 и E37, где указывался пол особей, образовывавших предыдущую пару. Если гермафродит оказывался в составе пары с самцом или гермафродитом, он, забеременевал и выходил из состава стада производителей. 

F29 — =E29 — вычисление количества самцов в составе стада производителей, которые могут участвовать в спариваниях. Это количество определяется их начальным количеством в стаде производителей, так как самцы не беременеют и могут размножаться много раз.

F30 — =E30-(ЕСЛИ(E36=3;ЕСЛИ(E37=1;1;ЕСЛИ(E37=2;1;0));0)+ЕСЛИ(E37=3;ЕСЛИ(E36=1;1;ЕСЛИ(E36=2;1;0));0)) — вычисление количества самок в составе стада производителей, которые могут участвовать в спариваниях. Аналогично таковому для гермафродитов.

F31 — =СУММ(F28:F30) — сумма трех предыдущих ячеек.

F32 — =ЕСЛИ(F31<2;0;ЕСЛИ(F36=1;(F28-1)*$N$19/((F28-1)*$N$19+F29*$P$19+F30*$R$19);0)+ЕСЛИ(F36=2;F28*$N$21/(F28*$N$21+(F29-1)*$P$21+F30*$R$21);0)+ЕСЛИ(F36=3;F28*$N$23/(F28*$N$23+F29*$P$23+(F30-1)*$R$23);0)) — с учетом того, что в ячейке F36 выбран первый партнер в паре, производится пересчет вероятности того, что второй партнер будет гермафродитом. $N$19 и другие ссылки указывают на ячейки, в которых задаются предпочтения при образовании пар. Если общая численность возможных партнеров в стаде производителей меньше двух, значение в ячейке будет равно 0.

F33 — =ЕСЛИ(F31<2;0;ЕСЛИ(F36=1;F29*$P$19/((F28-1)*$N$19+F29*$P$19+F30*$R$19);0)+ЕСЛИ(F36=2;(F29-1)*$P$21/(F28*$N$21+(F29-1)*$P$21+F30*$R$21);0)+ЕСЛИ(F36=3;F29*$P$23/(F28*$N$23+F29*$P$23+(F30-1)*$R$23);0)) — аналогично предыдущему; вероятность того, что второй партнер будет самцом.

F34 — =ЕСЛИ(F31<2;0;ЕСЛИ(F36=1;F30*$R$19/((F28-1)*$N$19+F29*$P$19+F30*$R$19);0)+ЕСЛИ(F36=2;F30*$R$21/(F28*$N$21+(F29-1)*$P$21+F30*$R$21);0)+ЕСЛИ(F36=3;(F30-1)*$R$23/(F28*$N$23+F29*$P$23+(F30-1)*$R$23);0)) — аналогично двум предыдущим; вероятность того, что второй партнер будет самкой.

F35 — =СЛЧИС() — генерируемое программой случайное число, находящееся в пределах от 0 до 1; используется для определения пола первого партнера в паре.

F36 — =ЕСЛИ(F31=0;0;ЕСЛИ(F35<F28/F31;1;ЕСЛИ(F35<(F28+F29)/F31;2;3))) — пол первого партнера в паре, который определяется случайным числом в предыдущей ячейке, в зависимости от количества потенциальных партнеров в составе стада производителей.

F37 — =ЕСЛИ((F32+F33+F34)=0;0;ЕСЛИ(F38<F32;1;ЕСЛИ(F38<(F32+F33);2;3))) — пол второго партнера в паре, который определяется с учетом предпочтений в выборе первого партнера на основании значений случайного числа в следующей ячейке.

F38 — =СЛЧИС() — генерируемое программой случайное число, находящееся в пределах от 0 до 1; используется для определения пола второго партнера в паре.

F39 — =ЕСЛИ(F36=1;ЕСЛИ(F37=1;$O$12;ЕСЛИ(F37=2;$O$13;ЕСЛИ(F37=3;$O$14;0)));0)+ЕСЛИ(F36=2;ЕСЛИ(F37=1;$O$13;ЕСЛИ(F37=2;$O$15;ЕСЛИ(F37=3;$O$16;0)));0)+ЕСЛИ(F36=3;ЕСЛИ(F37=1;$O$14;ЕСЛИ(F37=2;$O$16;ЕСЛИ(F37=3;$O$17;0)));0) — количество потомков-гермафродитов, определяемое в зависимости от состава пары.

F40 — =ЕСЛИ(F36=1;ЕСЛИ(F37=1;$P$12;ЕСЛИ(F37=2;$P$13;ЕСЛИ(F37=3;$P$14;0)));0)+ЕСЛИ(F36=2;ЕСЛИ(F37=1;$P$13;ЕСЛИ(F37=2;$P$15;ЕСЛИ(F37=3;$P$16;0)));0)+ЕСЛИ(F36=3;ЕСЛИ(F37=1;$P$14;ЕСЛИ(F37=2;$P$16;ЕСЛИ(F37=3;$P$17;0)));0) — количество потомков-самцов, определяемое в зависимости от состава пары.

F41 — =ЕСЛИ(F36=1;ЕСЛИ(F37=1;$Q$12;ЕСЛИ(F37=2;$Q$13;ЕСЛИ(F37=3;$Q$14;0)));0)+ЕСЛИ(F36=2;ЕСЛИ(F37=1;$Q$13;ЕСЛИ(F37=2;$Q$15;ЕСЛИ(F37=3;$Q$16;0)));0)+ЕСЛИ(F36=3;ЕСЛИ(F37=1;$Q$14;ЕСЛИ(F37=2;$Q$16;ЕСЛИ(F37=3;$Q$17;0)));0) — количество потомков-самок, определяемое в зависимости от состава пары.

После того, как была произведена имитация формирования 100 пар, вычисляются общие результаты года. Ячейки, в которых это делается, расположены в столбце A.

A31 — =СУММ(E39:CZ41) — общая сумма потомков, произведенных в данном году (на данном цикле работы модели).

A35 — =СУММ(E39:CZ39)/A31 — доля гермафродитов, произведенных на данном цикле модели.

A36 — =СУММ(E40:CZ40)/A31 — доля самцов, произведенных на данном цикле модели.

A37 — =СУММ(E41:CZ41)/A31 — доля самок, произведенных на данном цикле модели.

A39 — =A35*$R$7 — доля гермафродитов, доживающих до следующего года (с учетом их выживаемости, заданной в начальных параметрах).

A40 — =A36*$R$8 — доля самцов, доживающих до следующего года (с учетом их выживаемости, заданной в начальных параметрах).

A41 — =A37*$R$9 — доля самок, доживающих до следующего года (с учетом их выживаемости, заданной в начальных параметрах).

Итоги имитации на каждом цикле работы модели выносятся в блок ячеек, находящийся в крайней правой части листа. По формируемому таким образом набору чисел строится график, являющийся главной формой вывода результатов работы модели.

Пользоваться моделью очень просто. С использованием блока для определения начальных параметров необходимо задать набор исходных значений. После этого остается только нажать кнопку F9, подождать некоторое время, которое определяется быстродействием компьютера, и интерпретировать получившийся график. 

 

10.4. Популяційна динаміка і правило Гаузе (на межі можливостей електронних таблиць!)

10.4.1. Модель Gause-100

Автором этого пособия на базе Microsoft Excel сделана модель, описывающая взаимодействие четырех конкурирующих форм, которые могут относиться к одному или разным видам. К сожалению, независимый учет большого количества особей в модельной популяции требует достаточно большого объема вычислений. В представленной здесь модели рассматривается гильдия (т.е. совокупность форм, использующих один и тот же ресурс), состоящая из 280 или меньшего количества особей, каждая из которых относится к одной из четырех форм.

Саму модель (которая названа Gause-100) можно скачать здесь. Далее будет дано ее детальное описание. С одной стороны, это описание поможет в ходе экспериментов с этой моделью. Не менее важно то, что эта модель должна быть неким образцом для построения профессиональной модели, написанной на языке Python. Описание модели, выполненной в Excel, как надеется автор, поможен разработчикам ее расширенного аналога на Python или ином профессиональном языке программирования.

Модель служит для имитации популяционной динамики и конкуренции двух конкурирующих видов. В ней рассматривается взаимодействие четырех форм организмов (самок и самцов двух рассматриваемых видов). Каждая форма может быть представлена особями четырех разных возрастов (всего — 16 групп особей). Особи, относящиеся к одной группе (т.е. относящиеся к одной форме и имеющие один возраст) рассматриваются как идентичные.

Модель позволяет изменять несколько начальных параметров, характеризующих каждую группу особей, в том числе — задавать результаты их скрещивания.Из начального пула особей формируется рассматриваемая моделью гильдия (т.е. совокупность особей, в т.ч. разных видов, которые эксплуатируют один и тот же ресурс). Имитируется конкурентное сокращение численности в том случае, если потребности гильдии в ресурсах превышают емкость среды. Затем имитируется образование пар (из числа особей, способных участвовать в размножении, т.е. входящих в состав нерестового стада) и производство потомства. На следующем шаге имитации (в типичном случае соответствущем году) новый состав гильдии образуется из прежнего и потомства, появившегося на предыдущем шаге. 

10.4.2. Общая структура модели

Описываемая модель построена так, чтобы ее зона ввода-вывода помещалась на экране персонального компьютера, позволяя вносить изменения в начальные параметры и тут же наблюдать последствия этих изменений.

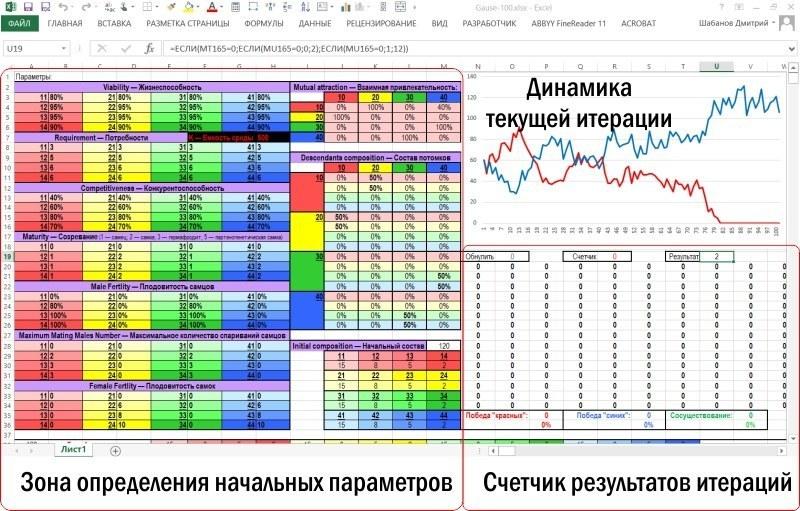
Сама модель занимает на листе Excel намного большее пространство

После зоны ввода-вывода располагается зона вычислений. Зона вычисления характеристик нерестового стада и выбор пар для размножения крупнее показан ниже. На рисунке виден блок строк, соответствующих первому году (устовному году, разумеется, точнее — шагу моделирования), и начало блока, соответствующего второму году.

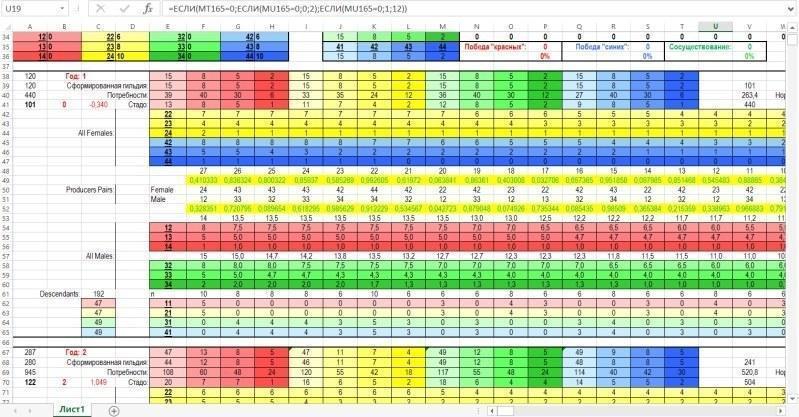
А на рисунке ниже показана зона, где вычисляется состав гильдии (всей совокупности особей) и нерестового стада (совокупности особей, участвующих в размножении).

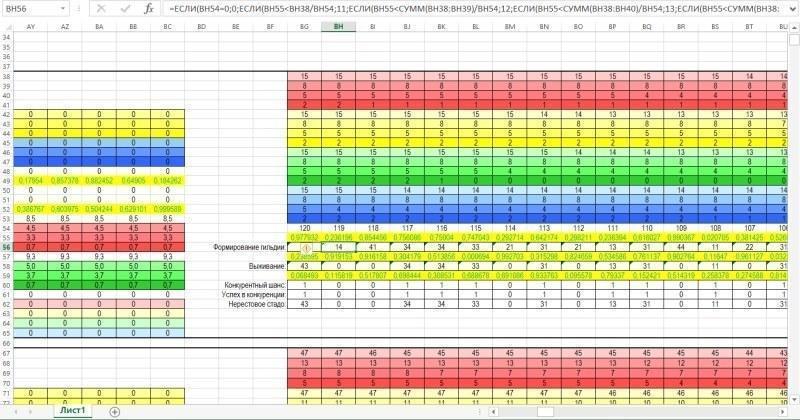
Наконец, на следующем рисунке показана зона, где собираются данные о динамике гильдии по результатам каждого года моделирования. Каждая строка этой зоны собирает данные из соответвующих строк зоны для вычислений. В последних двух столбцах вычисляется суммарная численность представителей двух видов. Эти столбцы служат цифровым материалом для построения диаграммы, находящейся в зоне ввода-вывода.

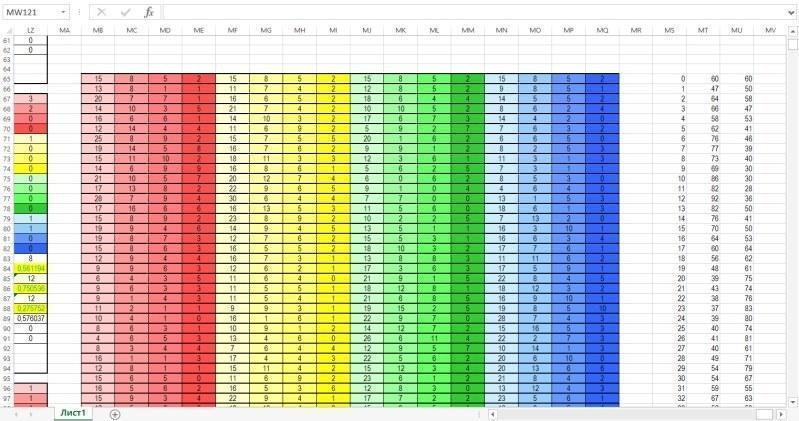
Параметры жизнеспособности в модели Gause-100:
— Viability (Жизнеспособность);
— Requirement (Потребности);
— Competitiveness (Конкурентоспособность);
— Maturity (Созревание);
— Male Fertlity (Плодовитость самцов);
— Maximum Mating Males Number (Максимальное количество спариваний самцов);
— Female Fertlity (Плодовитость самок).

 10.5. Требования к профессиональной модели Gause

10.5.1. Общая характеристика

Одна из главных причин написания планируемой модели заключается в том, что эксперименты с более простыми моделями (вначале экселевской модели Batrachometrics‑2010.xls, описанной тут, а потом —профессиональной модели Антона Леонова, коротко описанной тут, а несколько подробнее — в статье, находящейся в печати), был обнаружен эффект, о котором мы коротко сообщили в этой публикации. В наших экспериментах он обнаружен при изучении закономерности конкуренции межвидовых полуклональных гибридов и особей одного из родительских видов. Мы предполагаем, что это — часть более широкой закономерности, связанной с принципом конкурентного исключения Гаузе. Кстати, именно с этим связано название предлагаемой модели — "Gause".

Задача модели Gause — имитационное моделирование гильдий (совокупностей популяций, гемиклональных популяционных систем etc), позволяющее изучать влияние на их устойчивость конкуренции, гибридизации (в том числе — гемиклональной), разнообразия онтогенетических стратегий, разнообразия способов воспроизводства, разделения ниш и иных подобных популяционнобиологических феноменов.

В некоторых существенных аспектах работа профессиональной модели Gause (вероятно, написанной на языке Python), должна напоминать работу модели Gause-100. Тем не менее, смысл построения профессиональной модели в том, чтобы получить в результате ее создания значительно более широкие возможности для моделирования. В частности, эта модель должна: 

— имитировать динамику взаимодействия не четырех форм, а значительно большего их количества (например, 22); связано это с тем, что эта же модель должна быть пригодна для моделирования популяционных систем зеленых лягушек, включающих триплоидов (характерных для IV региона распространения зеленых лягушек в Левобережной Лесостепи Украины), а для этого потребуется моделировать достаточно большое количество генотипов; 

— предусматривать возможность для каждой группы особей задавать ее предпочтения относительно образования пар с представителями всех других групп;

— предусматривать среди возможных состояний признака "пол" варианты гермафродитизма и партеногенетических самок (в том числе тех, которым требуется для размножения спаривание с каким-либо самцом); это связано с тем, что создаваемая модель должна быть пригодна для моделирования эволюции раздельнополости, описанного в серии "половых" колонок: первой, второй, третьей, четвертой, пятой, шестой, седьмой, восьмой и окончанием;

— предусматривать возможность задавать динамику емкости среды (стохастичную; в соответствии с каким либо циклом; цикличную со стохастичной компонентой);

— предусматривать возможность переключения онтогенетических стратегий в зависимости от уровня конкурентности среды.

Последнее требование налагает серьезные ограничения на способ реализации модели. И в модели Batrachometrics, и в модели Антона Леонова как отдельные единицы рассматривались не особи, а группы, состоящие из идентичных особей (относящихся к одной форме и имеющие один возраст). В модели Gause-100 как отдельные единицы рассматриваются именно особи (хотя особи одной формы и возраста остаются идентичными). В модели Gause надо рассматривать как отдельные единицы именно особи, и при этом включать в характеристику каждой особи ряд ее признаков, прежде всего — характер ее онтогенетической стратегии. Это означает, что в модели должен быть предусмотрен механизм для определения этих стратегий и управления ими.

 

10.5.2. Онтогенетические стратегии особей

Важной причиной создания модели Gause служит моделирование онтогенетических стратегий. Прежде всего, следует разобраться в том, что они из себя представляют. В настоящее время лучше всего описаны видовые стратегии (в первую очередь  — r- и K-). Понятие стратегии остается запутанным. В самой общей форме стратегию можно определить, как иерархию приоритетов (подробнее — здесь). Наиболее распространены представления о стратегиях, как о разных вариантах выбора между поддержанием организмом себя самого и воспроизведением себя в потомках. Разнообразие зеленых лягушек и многих других животных по скорости их роста, возрасту начала размножения, плодовитости и продолжительности жизни можно описать как проявления онтогенетических стратегий. Понятие онтогенетических стратегий вводится в этой статье; там же приведено описание стратегий тугорослости и скороспелости. В соответствии с начальными предположениями мы ожидали, что две альтернативные стратегии могут быть описаны следующим образом.  

Стратегии   Параметры	Тугорослость	Скороспелость
Скорость роста
Возраст начала размножения
Плодовитость за сезон
Продолжительность жизни

 

Анализ скелетохронологических данных, полученных при изучении зеленых лягушек, заставил откорректировать этим представления. Ниже приведена таблица, где сравниваются две стратегии зеленых лягушек (статья, откуда она взята, находится на момент написания данной страницы в печати). 

 

ВОС   Характеристики	Малоразмерность (undersized)		Крупноразмерность (oversized)
	Самки	Самцы	Самки	Самцы
Размеры	Относительно меньшие: lL = 9,7 + 8,3×A		Относительно бóльшие: bL = 32,5 + 8,3×A
Скорость роста в возрасте 3–4 года	Относительно низкая: lgme3 = 0,170; lgme4 =0,176		Относительно высокая: bgme3 =0,450; bgme4 =0,288
Полноценное участие в нересте	Относительно раннее: с 4 лет	Относительно позднее: с 6 лет	Относительно позднее: с 6 лет	Относительно раннее: с 5 лет
Продолжительность жизни	Относительно высокая: до 10 лет		Относительно низкая: до 8 лет
Плодовитость самок	Относительно низкая: F = ‑1325 + 335×A	‒	Относительно высокая: F = 179 + 316×A	‒
Количество сезонов размножения	Особо большое: до 7 лет	Относительно большое: до 5 лет	Особо малое: до 3 лет	Относительно малое: до 4 лет

 

Описывая онтогенетические стратегии, мы вычисляем для каждой особи (в зависимости от ее размера) параметр Strategy. Он равен 1, если размер особи соответствует типичному для стратегии крупноразмерности, и -1, если он типичен для малоразмерности. 

Вероятно, следует моделировать различия особей по их онтогенетическим стратегиям следующим образом. Параметр Strategy должен стать одной из характеристик каждой особи. На настоящее время неизвестно, как он определяется в действительности. Можно предположить, что этот признак, как и подавляющее большинство иных ключевых характеристик особи, зависит частично от генотипа особи, и частично от средовых воздействий на нее. Модель Gause должна предусматривать возможность имитирования обоих этих механизмов.

 

10.5.3. Моделирование онтогенетических стратегий

В зависимости от предыстории особи определяется характерное для нее значение переменной Strategy. В зависимости от этого значения и возраста особи определяется ее жизнеспособность, размер и участие в нересте и плодовитость. Вероятно, надо предусмотреть возможность для каждого из 22 генотипов задавать два разных варианта, соответствующих крайним значениям параметра Strategy (например, от +3 до -3). Естественно, нужно предусмотреть и возможность не задавать такую вариативность.

Если стратегия определяется только принадлежностью к определенной форме, особей с разными стратегиями можно рассматривать, как относящихся к разным формам, для которых задавать разные значения параметров.

Если стратегия определяется только средой, для каждой формы надо задать крайние значения, и предусмотреть функцию, которая корректирует значение параметра Strategy в определенном возрасте в зависимости от определенной характеристики модельной гильдии (вероятнее всего — от остроты конкуренции).

Сложнее всего реализовать вариант, при котором стратегия определяется частично генетической предрасположенностью, а частично — влиянием среды. Конкретного решения этой проблемы у меня на момент написания этих строк нет. Один из вариантов таков: в характеристики каждой особи включить состояние ее нескольких генов. Значение параметра Strategy (и, возможно, иных параметров, прежде всего — описывающих эффективность потребления разных частей ресурсного спектра, как это описано в следующем пункте) определять по правилам, учитывающим состояние этих генов. Впрочем, способ реализации этого варианта еще надо обсуждать.

 

10.5.4. Моделирование разделения ниш

Поскольку одной из задач программы Gause является моделирование конкурентного исключения по Гаузе, в этой модели должен быть предусмотрен механизм разделения их экологических ниш. В данном случае, экологическая ниша — это характер связи популяции с ее средой; разделение экологических ниш связано с дифференциацией ресурсных ниш, т.е. совокупностей потребляемых ресурсов.

В соответствии с классическими представлениями, сосуществование конкурирующих видов может быть связано с тем, что они специализируются на потреблении разных частей спектра общих ресурсов. К примеру, и вид А, и вид В, существуюя сами по себе, могут потреблять весь спектр доступных ресурсов (например, питаться как маленькими, так и большими жертвами, или питаться в течение всех суток). Правило Гаузе заключается в том, что если эти два вида обитают вместе, устойчивость их сосуществования может быть обеспечена тем, что они делять ресурсные ниши: например, вид А питается мелкими жертвами, а вид В — крупными, или вид А питается днем, а вид В — ночью. Две-три переменных, по которым происходит разделение ниш (например, размер жертв, способ их добычи и время их добычи) позволяют обеспечить устойчивое сосуществование гильдий, состоящих из двухзначного количества популяций.

Я предлагаю использовать один параметр (размер добычи; впрочем, его можно интерпретировать и как-то иначе), состоящий, к примеру, из 12 ресурсных категорий. Емкость среды (количество доступных ресурсов) задается отдельно для этих двенадцати категорий (двенадцатью числами, а не одним, как в модели Gause-100). В параметры каждой формы входит эффективность потребления каждой из этих двенадцати категорий.

Следствием из этого изменения алгоритма оказывается то, что прежний алгоритм конкурентного сокращения численности (которым мы гордились), нуждается в замене или изменении.

Один из вариантов таков. Каждая категория ресурса делится между всеми группами-потребителями (отличающимися по принадлежности к определенной форме и по возрасту), которые ее эксплуатируют, пропорционально их численности и эффективности потребления этой категории ресурса. Определяется количество ресурса, полученного каждой группой. Происходит конкурентное сокращение особей этой группы, при котором шансы каждой особи на выживание пропорциональны их конкурентоспособности. В простейшем случае конкурентоспособность особей одной группы одинакова, однако в том случае, если особи внутри группы отличаются по их онтогенетическим стратегиям, их конкурентоспособность может быть различной.

Недостатком этого алгоритма является то, что в случае конкуренции многочисленных групп уменьшится вероятность резкого сокращения или увеличения численности какой-то из них. Надо решить, можно ли моделировать эффект случайных отклонений при дискретизации вероятностей в малых выборках. 

 

10.5.5. Особенности интерфейса

Ввод данных в модель должен осуществляться через пять таблиц:

— значения параметров жизнеспособности для рассматриваемых форм особей;

— распределения вероятностей выбора друг друга особями разных форм (и возрастов?) при образовании пар;

— распределения вероятностей образования потомков от всех возможных вариантов скрещивания;

— начальный состав гильдии и закланированный характер иммиграции (прибытия определенных особей в рассматриваемую гильдию);

— состав и динамика ресурсов среды.

Непростой проблемой при проектировании модели Gause является проектирование ее интерфейса. Предположим, в модели рассматриваются 22 формы особей. Предложенное количество особей не избыточно. К примеру, в модели Batrachometrics рассматривается 13 форм: ^XL^XL, ^XL^YR, ^XR^XR, ^XR^YR, ^XR(^XL), ^YR(^XR), ^XR(^YL), ^XL(^XR), ^YL(^XR), ^XL(^YR), (XL)(XR), (^XL)(^YR), (^YL)(^XR). В модели Антона Леонова рассматривается тот же набор форм, но он остается открытым: туда можно добавлять новые формы (но, увы, в настоящее время неудобным для пользователя образом). Анализ триплоидов потребовал бы добавления к их числу целого ряда новых форм. Для каждой формы следует предусмотреть тут или иную продолжительность жизни. У зеленых лягушек максимальная зарегистрированная нами продолжительность жизни составляет 10 лет; при использовании модели для изучения каких-то иных форм следует предусмотреть существенно большую продолжительность жизни. Например, у серых жаб, на примере которых мы тоже изучаем онтогенетические стратегии, максимальная продолжительность жизни составляет не менее 15 лет. Предположим, мы рассматриваем 22 формы особей (11 видов в случае, если гибридизация отсутствует) с максимальной продолжительностью жизни 16 лет. Это означает, что в модели рассматривается 352 возрастные группы. Для каждой из них надо задать набор параметров жизнеспособности. В модели Gause-100 используются 7 параметров жизнеспособности. Если в модели Gause останется то же количество параметров (на самом деле, их количество должно измениться, но не принципиально), это будет означать, что, задавая параметры жизнеспособности, надо заполнить 2464 ячеек. Ситуацию усугубляет то, что как минимум для некоторых из этих ячеек надо задавать два значения: соответствующее скороспелости и соответствующее тугорослости. Итак, их максимальное количество может превысить 5 тысяч. Чтобы работа по вводу такого количества данных была выполнимой и осмысленной, нужно предусмотреть несколько механизмов, в числе которых:

— автоматическое заполнение ячеек в соответствии с тем или иным шаблоном (должна быть возможность создать несколько шаблонов значений параметров жизнеспособности, а потом указать для каждой формы подходящий для нее шаблон и тем самым обеспечить автоматическое заполнение ее ячеек);
— корректировка автоматически заполненных ячеек после применения определенного шаблона;
— автоматическое выключение неиспользуемых ячеек (когда количество форм менее 22 или максимальная продолжительность жизни менее 16 лет);
— экспорт заполненных таблиц жизнеспособности в простой формат (например, *.csv) и их импорт.

Еще серьезнее проблема определения вероятностей выбора особями друг друга при образовании пар. При принятых условиях в модели должно рассматриваться 22×22=484 парных сочетаний форм. Однако и этого количества может быть недостаточно. Во многих случаях существенным обстоятельством, определяющим потенциальную привлекательность партнера, является его возраст (точнее, не возраст, но связанные с возрастом параметры).

При определении состава потомства от скрещиваний потенциально следует рассматривать 22×22×22=10648 ячеек (для каждого варианта попарного скрещивания 22 двух форм необходимо указать вероятность появления в потомстве каждой из 22 форм). Впрочем, очевидно, что в подавляющем большинстве случаев большинство этих ячеек будет неиспользуемым. Чаще всего будут моделироваться ситуации, в которых будут рассматриваться формы, относящиеся к самкам и самцам; в этом случае, заполнять следует только те ячейки, которые соответствуют скрещиванию самца и самки. При моделировании ситуаций, в которых рассматриваются гермафродиты, способные к гибридизации разных форм, надо будет использовать все ячейки; более того, их количество нельзя даже сократить вполовину, потому что потомство,от скрещивания двух гермафродитичных форм А и В может быть разным, в зависимости от того, какой из гермафродитичных родителей выполнял для потомков материнскую роль, а какой — женскую.