Кравченко М. А., Шабанов Д. А. Моделирование трансформаций гемиклональных популяционных систем зеленых лягушек (Pelophylax esculentus complex; Amphibia, Ranidae) с помощью рекуррентных разностных уравнений // Вісник Харківського національного університету імені В. Н. Каразіна. Серія: біологія. – 2010. – Вип.12 (№920). – С. 70–82.
УДК: 004.942:597.851
Моделирование трансформаций гемиклональных популяционных систем зеленых лягушек (Pelophylax esculentus complex; Amphibia, Ranidae) с помощью рекуррентных разностных уравнений
М.А.Кравченко, Д.А.Шабанов
Харьковский национальный университет имени В.Н.Каразина (Харьков, Украина)
m_kravchenko@inbox.ru, d.a.shabanov@gmail.com
Описаны принципы построения математической модели гемиклональных популяционных систем европейских зеленых лягушек. Модель с дискретным временем и перекрывающимися поколениями основана на рекуррентных разностных уравнениях. Для всех генотипов задается набор параметров жизнеспособности (продолжительность жизни, срок первого нереста, конкурентоспособность, вероятность размножения, плодовитость и др.). После вычисления смертности представителей всех возрастных классов рассматриваемых генотипов моделируется их размножение и происходит переход к следующему шагу модели и повторение описанной процедуры. Модель реализована средствами MS Excel. Представлены примеры трансформаций состава моделируемых систем.
Ключевые слова: Pelophylax esculentus(= Rana esculenta) complex, гемиклональные популяционные системы, моделирование,гемиклональное наследование, гибридизация, MS Excel.
Моделювання трансформацій геміклональних популяційних систем зелених жаб (Pelophylax esculentus complex; Amphibia, Ranidae) за допомогою рекурентних різницевих рівнянь
М.О.Кравченко, Д.А.Шабанов
Описано принципи побудови математичної моделі геміклональних популяційних систем європейських зелених жаб. Модель з дискретним часом та поколіннями, що перекриваються, заснована на рекурентних різницевих рівняннях. Для всіх генотипів задається набір параметрів життєздатності (тривалість життя, термін першого нересту, конкурентоспроможність, вірогідність розмноження, плодючість та ін.). Після обчислення смертності представників всіх вікових класів даних генотипів моделюється їх розмноження і відбувається перехід до наступного кроку моделіта повторення описаної процедури. Модель реалізована засобами MS Excel. Представлено приклади трансформацій складу модельованих систем.
Ключові слова:Pelophylax esculentus(= Rana esculenta) complex, геміклональні популяційні системи, моделювання, геміклональне спадкування, гібридизація, MS Excel.
Modeling the transformations of water frogs (Pelophylax esculentus complex; Amphibia, Ranidae) hemiclonal population systems by the use of recurrent difference equations
M.O.Kravchenko, D.A.Shabanov
Construction principles of mathematical models of hemiclonal population systems of the European water frogs are described. A model implying discrete time and overlapping generations is based on the recursion difference equations. For all genotypes the complex of viability parameters (life-span, term of the first spawning, competitiveness, probability of reproduction, fecundity and other) is set. At first death rate of representatives of all age-dependent classes of the examined genotypes is calculated. Then reproduction of these genotypesis simulated and the model passes to the next step and reiteration of the described procedure. A model is designed by the means of MS Excel. Еxamples of transformations of the simulated systems composition are presented.
Key words:Pelophylax esculentus (= Rana esculenta) complex, hemiclonal population systems, modeling, hemiclonal inheritance, hybridization, MS Excel.
Постановка проблемы
Европейские зеленые лягушки, Pelophylax esculentus complex, в последние десятилетия привлекают исключительное внимание исследователей. Два родительских вида, прудовые, Pelophylax lessonae (Camerano, 1882), и озерные, Pelophylax ridibundus (Pallas, 1771), лягушки при скрещивании порождают гемиклональные межвидовые гидриды, съедобных лягушек, Pelophylax esculentus (Linnaeus, 1758). Выделение рода (ранее – подрода) Pelophylax из состава рода Rana обосновано относительно недавно (Frost etal., 2006). Более привычными названиями этих животных являются Rana lessonae, Rana ridibunda и Rana esculenta. Серьезные дискуссии касаются корректного названия гибридных лягушек. Не вступая в эти споры, мы подчеркиваем, что используем для межвидовых гибридов название, аналогичное видовому, в значительной мере условно.
У P. esculentus, в отличие от подавляющего большинства животных, в гаметы (половые клетки) попадают не рекомбинантные геномы, состоящие из фрагментов геномов обоих родительских видов, а преимущественно один или другой из родительских геномов в чистоте, клонально (Plötner, 2005). Представители P. esculentus относятся к различным кариогенетическим формам. Например, значительное количество различных форм P. esculentus зарегистрировано в Северско-Донецком центре разнообразия зеленых лягушек, расположенном в бассейне верхнего течения р. Северский Донец. Обозначим буквой L геном P. lessonae, буквой R –геном P. ridibundus, а также будем показывать клональность генома заключением его символа в скобки. Можно указать, что в Северско-Донецком центре разнообразия зеленых лягушек зарегистрированы такие кариогенетические формы P. esculentus: (L)R, L(R), (L)(R), LLR, LRR и даже LLRR (Borkin et al., 2004; Боркин и др., 2005).
Различные представители Pelophylax esculentus complex, хотя и отличаются по своим экологическим особенностям (Коршунов, 2008), способны обитать совместно, скрещиваясь друг с другом. При этом образуются особые биосистемы, где особи разных видов и форм объединяются совместным воспроизводством – популяционные системы. Чтобы подчеркнуть своеобразие этих систем, поддерживающихся благодаря гемиклональному наследованию, такие биосистемы было предложено (Шабанов и др., 2009) называть гемиклональными популяционными системами – ГПС. В ГПС передаются как обычные, рекомбинантные геномы, так и клональные. Вероятно, передача клональных геномов может происходить в течение длительного времени. Так, в Северско-Донецком центре разнообразия зеленых лягушек, несмотря на специальные поиски, не зарегистрированы половозрелые представители P. lessonae. Перечисленные выше формы гибридов обитают здесь совместно с P. ridibundus, передавая геномы (L) клонально на протяжении многих поколений.
В ходе исследований естественных ГПС зеленых лягушек в ряде случаев была зарегистрирована смена их состава с течением времени. Одна из таких ГПС населяет Иськов пруд в с. Гайдары Змиевского р-на Харьковской области, в окрестностях биостанции Харьковского национального университета им. В. Н. Каразина и Национального природного парка «Гомольшанские леса» (Шабанов и др., 2006). Вероятно, и состав иных ГПС не сложился сразу таким, как его можно сейчас наблюдать, а является результатом трансформаций во времени. Трансформации состава ГПС – длительные процессы, и непосредственное наблюдение за ними является весьма сложной задачей. Для их реконструкции полезна математическая модель ГПС.
Механизмы, которые приводят к гемиклональному наследованию, до сих пор изучены недостаточно. Например, до сих пор не до конца ясны закономерности, позволяющие по составу геномов гибридных лягушек определить, какие гаметы они будут производить. Моделирование может помочь даже в решении таких вопросов. Модель строится на основе определенной совокупности представлений о системе-оригинале (естественно, значительно упрощающих действительность, но отражающих ее существенные особенности). Результатом работы модели является зависящий от исходных условий набор конечных состояний моделируемых систем. Можно предположить, что если исходные предположения неадекватны или внутренне противоречивы, модель будет порождать иные наборы состояний, чем состояния ГПС, регистрируемые в естественных условиях. Соответствие работы модели и эмпирических данных о системе-оригинале является косвенным доказательством адекватности представлений о системе-оригинале, использованных при построении модели.
Особенности зеленых лягушек, которые необходимо учесть при моделировании
Европейские зеленые лягушки размножаются раз в год, весной или в начале лета (Ананьева и др., 1998). Половозрелые самки и самцы выходят с зимовки, начинают питаться, а затем собираются на местах нереста, образуя пары. Во многих работах показана избирательность лягушек в образовании пар. За крупных самок развивается более острая конкуренция самцов; самцы с разным уровнем агрессивности имеют разные шансы на успех. При образовании пары самец удерживает самку в состоянии амплексуса, обхватывая ее передними конечностями. Самка выбрасывает в воду икру, а самец поливает ее молоками (сперматозоидами, выбрасываемыми в воду). Размер кладки зависит от особенностей самки; иногда часть икринок могут быть нежизнеспособными. Молоки самца могут содержать большее или меньшее количество нормальных сперматозоидов; иногда оказываются оплодотворены не все икринки в кладке. Самка, отложив свою икру в одной или нескольких порциях, уходит с нерестилища, а самец может остаться на нем и искать других самок.
Из оплодотворенных икринок выходят головастики. Обычно количество головастиков многократно превосходит количество лягушек после метаморфоза. Разнообразные хищники и неблагоприятные условия (наподобие пересыхания нерестовых водоемов или их отделившихся при обмелении участков) часто приводят к их массовой неселективной (мало зависящей от особенностей отдельных индивидов) гибели. В течение первого же лета головастики проходят личиночное развитие и претерпевают метаморфоз, превращаясь в сеголетков. Зачастую сеголетки массово гибнут в результате действия разнообразных неблагоприятных факторов, прежде всего – хищников (в том числе – лягушек старших возрастных классов). Летом и в начале осени лягушки питаются, получая энергию, необходимую для роста, зимовки и, в случае половозрелых особей, – образования половых продуктов. Половозрелости лягушки достигают в определенном возрасте, вероятно, различном для разных особей и зависящем от пола, кариогенетической формы, генотипа и условий развития.
Зиму лягушки проводят или в убежищах на суше, или на дне непромерзающих водоемов. В это время их рост останавливается, и в их костях образуются линии склеивания (свидетельства зимней остановки роста), позволяющие определить возраст каждой особи (Смирина, 1983). Половозрелые особи отправляются на места нереста (и, вероятнее всего, будут нереститься каждый год до конца своей жизни). Рост лягушек продолжается всю жизнь, но после половозрелости его относительная скорость снижается. Год от года численность возрастных классов сокращается вследствие смертности. Максимальная продолжительность жизни зеленых лягушек в естественных местообитаниях вряд ли существенно превышает 10 лет (Усова, 2010) или 12 лет (Шалдыбин, 1976).
К сожалению, до сих пор недостаточно известно, какие факторы ограничивают численность лягушек в определенном местообитании. В неблагоприятной абиотической среде сдерживать рост численность лягушек будет смертность от губительных факторов. Вероятно, если условия благоприятны и выживает избыточное количество особей, их численность будут сокращать разнообразные зависящие от плотности популяции факторы (Шабанов, Кравченко, 2009). В их числе конкуренция за ресурсы, каннибализм, переключение хищников-полифагов на питание лягушками, размножение хищников-олигофагов, избыточное распространение паразитов и, наконец, эмиграция в другие местообитания.
Разностные уравнения для описания популяционной динамики
Для изучения динамики ГПС лягушек адекватна модель с дискретным временем (с шагом в 1 год – от нереста до нереста) и перекрывающимися поколениями (Ризниченко, 2003).
В смешанных ГПС, например в Северско-Донецком центре разнообразия зеленых лягушек, совместно обитают разные формы этих животных. Значит, в модели необходимо отслеживать их численность по отдельности. Поскольку свойства особи (участие или неучастие в нересте, плодовитость и т.п.) зависят от ее возраста, необходимо вести учет особей каждого возраста (и определенной формы) по отдельности. При размножении самки и самцы всех представленных на нересте форм скрещиваются случайно, но с разной вероятностью, зависящей от привлекательности самок и агрессивности самцов. Состав потомства определяется сочетанием тех половых клеток, которые производят самки и самцы. В ряде случаев в потомстве от скрещивания одних форм лягушек могут появляться представители иных форм (примеры подобных случаев приведены ниже).
Для описания важных для моделирования ГПС лягушек демографических параметров используется ряд обозначений (табл. 1). Некоторые из этих обозначений общеприняты, для других символы подобраны по подходящим (непосредственно или метафорически) английским словам, для каких-то пришлось использовать оставшиеся свободными буквы латиницы.
Можно утверждать (по Бигон и др., 1989, с несущественными изменениями), что в момент времени t численность определенной группы особей в ограниченном местообитании (Nt) зависит от ее численности на предыдущем этапе t-1(Nt-1) так:
Nt = Nt-1 - D + B + I - E.
Как уже сказано, вычисления в соответствии с подобными уравнениями следует проводить на каждый шаг модели (соответствующий году) для каждого возраста и генотипа лягушек, которые могут быть представлены в модели. Установим, что группу особей можно выделить по их генотипу (1G, 2G, … jG…) и возрасту (a, a+1 и т.д.). Обозначать такие группы мы далее будем так:jGa; здесь левый верхний индекс отражает номер генотипа, а нижний правый — возраст. Одни из генотипов приводят к развитию самок, а другие – самцов. Здесь и далее прописные буквы для указанных в табл. 1 параметров или переменных используются для обозначения этих величин в целом, а строчные – для обозначения этих же величин, относящихся к определенным группам особей, выделенных по генотипу или/и возрасту. К примеру, Wt – это численность всех «перезимовавших» к году t лягушек, а w(jGa) – численность в этом же году перезимовавших лягушек возраста a с генотипом j.
Таблица 1. Использованные в работе обозначения демографических параметров и переменных в модели (букве K в ее прописном и строчном написании соответствуют различные значения; буквы X и Y в их прописном написании имеют иное значение, чем в виде индексов)
|
Символ |
От англ. |
Значение |
|
A |
Age |
Возраст |
|
B |
Birth rate |
Рождаемость |
|
C |
Competitiveness |
Конкурентоспособность |
|
D |
Death-rate |
Смертность |
|
E |
Emigration |
Эмиграция |
|
F |
Fecundity |
Плодовитость |
|
G |
Genotype |
Генотип |
|
H |
- |
Количество потенциально участвующих в амплексусах особей одного пола |
|
I |
Immigration |
Иммиграция |
|
j |
- |
Обозначение для одного из генотипов (j-того генотипа) в модели |
|
K |
- |
Емкость среды (количество доступных ресурсов) |
|
k |
- |
Коэффициент для пересчета параметра с возрастом |
|
L |
Life-span |
Продолжительность жизни |
|
M |
Maturity |
Год первого нереста |
|
N |
Number |
Численность (окончательная, после сокращений) |
|
O |
Overcharge |
Потребность в ресурсе до конкурентного сокращения |
|
P |
Posterior |
Суммарная вероятность последующих амплексусов |
|
Q |
Quota |
Нормированный (по конкурентоспособности) остаток численности после сокращения |
|
R |
Reproduction |
Вероятность размножения |
|
S |
Survivability |
Выживаемость |
|
T |
Time |
Дискретное время модели |
|
U |
Use |
Использование ресурсов |
|
V |
Vestiges |
Окончательная потребность в ресурсах после сокращения численности |
|
W |
Wintering |
«Входная» численность, к-во перезимовавших (до конкурентного сокращения) |
|
X |
- |
Количество амплексусов, состоявшихсяв определенном году |
|
X |
- |
Индекс, обозначающий женскую половую хромосому (X-хромосому) |
|
Y |
Yoke |
Количество ресурсов, требуемое после нормированного сокращения |
|
Y |
- |
Индекс, обозначающий мужскую половую хромосому (Y-хромосому) |
|
Z |
- |
Нормированное (по вероятности размножения) к-во амплексусов избыточного пола |
Численность группы особей jGa в момент времени t обозначим n(jGa)t. Тогда
n(jGa)t = n(jGa-1)t-1 – d(jGa)t + b(jGa)t + i(jGa)t + e(jGa)t.
Аналогично следует определять численность всех генотипов и всех возрастов, за исключением особей возраста 0, которые образуются в результате размножения. Естественно, для каждой группы необходимо предусмотреть уравнения, по которым вычисляются величины B, D, C и E для каждого промежутка дискретного времени модели. Условно принята такая последовательность расчетов.
0. Вычисляется численность всех групп лягушек в прошлом году, например, n(jGa-1)t-1.
1. Лягушки зимуют. Из зимовки выходит сокращенное (в соответствии с параметром выживаемости, S, см. ниже) количество особей: w(jGa)t и т.д.
2. Численность лягушек может сокращаться в результате конкуренции. В таком случае вычисляется сокращенная численность особей, нормированная по конкурентоспособности: q(jGa)t и т.д.
3. Определяется численность лягушек в текущем году n(jGa)t и т.д. Если это предусмотрено, к ней прибавляются особи-иммигранты.
4. Происходит образование пар в амплексусе.
5. Происходит образование потомства, состав которого зависит от состава пар в амплексусе, и появление особей возрастного класса 0.
После этого цикл повторяется.
Вероятно, оптимальным представляется вариант, когда все вычисляемые величины однозначно определяются численностью особей на том этапе, к которому они относятся, а также набором изначально заданных параметров. Модель будет более простой и легче интерпретируемой, если каждая из этих величин будет вычисляться в ходе одной и той же процедуры для всех генотипов. Необходимо, чтобы различия между генотипами определялись параметрами, которые экспериментатор задает во время использования модели.
Параметры жизнеспособности
Назовем характеризующие группы особей величины, которые используются при вычислениях их рождаемости и смертности, параметрами жизнеспособности. Для каждого генотипа по отдельности в модели задается комплекс таких параметров, охарактеризованный в табл. 2.
Таблица 2. Комплекс параметров жизнеспособности, задаваемых в модели для каждого генотипа (на примере генотипа jG)
|
Параметры жизнеспособности |
|
Прирост |
Значение параметра для особей возраста а: |
||
|
a=1 |
a=2 (для S и С); a=M (для R, F, P) |
a>2 (для S и С); a>M (для R, F, P) |
|||
|
Продолжительность жизни (L) |
L(jG) |
|
|
|
|
|
Возраст 1-го нереста (M) |
M(jG) |
|
|
p1(jGM) = P(jG) |
|
|
Выживаемость (S) |
S(jG) |
kS(jG) |
s1(jG) |
s1(jG) = S(jG) |
s(jG) = s(jGa-1) + kS(jG) × (1 - s(jGa-1)) |
|
Конкурентоспособность (C) |
C(jG) |
kC(jG) |
c1(jG) |
c1(jG) = C(jG) |
c(jG) = c(jGa-1) + kC(jG) × (1 - c(jGa-1)) |
|
Использование ресурсов (U) |
|
|
Задается отдельно для каждого возраста |
||
|
Вероятность размножения (R) |
R(jG) |
kC(jG) |
|
r1(jGM) = R(jG) |
r(jG) = r(jGa-1) + kR(jG) × (1 - r(jGa-1)) |
|
Плодовитость (F) |
F(jG) |
kF(jG) |
|
f1(jGM) = F(jG) |
f(jG) = f(jGa-1) + kF(jG) × f(jGa-1) |
|
Вероятн. повторных амплексусов (P) |
P(jG) |
kP(jG) |
|
p1(jGM) = P(jG) |
p(jG) = p(jGa-1) + kP(jG) × p(jGa-1) |
|
Характер определения в модели |
Задается для каждого генотипа |
Вычисляется для каждого возраста на основе заданных параметров |
|||
Показанные в табл. 2 параметры можно разделить на три группы. Продолжительность жизни и время нереста характеризуют представителей генотипа в целом и не пересчитываются для каждого возраста по отдельности. Время первого нереста тесно связано со сроком наступления половозрелости. Разница между ними состоит в том, что половозрелость достигается летом или осенью в возрасте M-1, а затем в зимовку особь уходит с половыми продуктами, которые использует во время своего первого нереста в возрасте M.
Следующие параметры определяют смертность (и эмиграцию, которая в модели не рассчитывается отдельно, а суммируется с «истинной» смертностью). В данном случае выживаемость – это доля особей, которые доживают до следующего года в условиях, где нет конкуренции; величина S изменяется в диапазоне от 0 (гибнут все) до 1 (все остаются живы).
В определенных случаях численность особей превышает емкость экосистемы. В ответ на это должны возрастать зависимые от плотности факторы, приводящие к смерти или эмиграции особей. В любых моделируемых популяциях и смешанных популяционных системах будут оказываться представители разных генотипов (в простейшем случае одновидовой популяции – генотипы, приводящие к развитию самок или самцов). Сокращение их численности потенциально может быть различным, зависящим от устойчивости к нехватке ресурсов. Эта устойчивость задается параметром конкурентоспособности C, который также изменяется от 0 до 1. Этот параметр показывает вероятность того, что сокращение численности особей будет происходить за счет представителей данного генотипа.
В жизненном цикле бесхвостых амфибий основная смертность характерна для икры, головастиков и сеголеток – особей возраста 0. Для этого возрастного класса выживаемость и конкурентоспособность задаются отдельно и условно переносятся к моменту выхода с зимовки в следующем году (как s(jG1)). Изменение выживаемости и конкурентоспособности с возрастом для остальных возрастных классов учитывается с помощью приведенных в табл. 2 поправок и учитывающих их формул.
Наконец, параметр U определяет тот ресурс, исчерпание которого запускает конкурентное сокращение численности. Следует отметить, что исследования, которые определяли бы, какой именно параметр определяет емкость среды для бесхвостых земноводных, авторам неизвестны. В логистической модели емкость среды (K) – это максимальная численность популяции, для которой в местообитании достаточно ресурсов. Очевидно, что один сеголеток не эквивалентен семилетней половозрелой особи. Но сколько же сеголетков эквивалентно семилетке? Если бы все лягушки питались одной и той же пищей, и конкуренция была бы следствием исчерпания доступных для них жертв, то оптимальный подход заключался бы в определении пищевого ресурса, потребляемого каждой особью. В нашей модели в данное время значение параметра U задается так, чтобы оно было пропорционально биомассе лягушек данного возраста для рассматриваемого генотипа. В то же время, поскольку этот параметр задается таблично, отдельно для каждой категории особей, модель может быть легко перестроена под иную оценку вклада каждой особи в исчерпание общих ресурсов.
Последние три параметра влияют на размножение (и, значит, рождаемость) лягушек. Как уже указывалось, разные самки отличаются друг от друга по вероятности их размножения (что проявляется в случае нехватки самцов). Подобным же образом отличаются друг от друга и самцы. Шанс каждой особи вступить в амплексус будет пропорционален параметру M (с учетом возрастной поправки). Данный параметр принимает значения от 0 до 1. Плодовитость самок зеленых лягушек измеряется сотнями и тысячами произведенных икринок и задается соответствующим положительным числом. Плодовитость самцов определяется долей икринок самки, которую они могут оплодотворить, и изменяется от 0 до 1. Плодовитость самок с возрастом должна, по всей видимости, возрастать, а самцов – оставаться постоянной (значение поправки kF для них равно 0). Последний параметр, P, вероятность повторных амплексусов, приложим только к самцам (у самок он всегда равен 0). Поскольку один самец может оплодотворить более одной самки, необходимо учитывать и эту величину (не делая принципиального отличия между вторым и третьим амплексусом одного самца, а учитывая сумму вероятности всех повторных амплексусов). Эта величина также может изменяться с возрастом самца.
Характер вычисления поправки на возраст (см. последний столбец в табл. 2) различается для разных параметров жизнеспособности. Для тех параметров, которые представляют собой вероятности с верхним пределом их значения 1, поправка каждого года уменьшает на заданную долю разницу между достигнутой приспособленностью и единицей. Плодовитость для обоих полов и суммарная вероятность повторных амплексусов для самцов просто возрастают на заданную долю.
Алгоритм конкурентного сокращения численности
Рассмотрим совокупность особей, имеющих генотипы 1G, 2G, … jG. Эти особи представлены разными возрастными группами: 1Ga-1, 1Ga, 1Ga+1,…jGa-1, jGa, jGa+1.
Для каждой из этих групп в соответствии с приведенными в табл. 2 данными рассчитаны значения их выживаемости (s(jG) и т.д.) и конкурентоспособности: (c(jG) и т.д.). Для каждой группы задано потребляемое их представителями количество ресурсов (пропорциональное биомассе или продуктивности): (u(jG) и т.д.). Каждая из этих групп характеризуется определенной численностью (n(jG) и т.д.). Принимается условие, что суммарное (по всем генотипам и возрастам) потребление ресурсов V не должно превышать емкость среды: V = Σ(n(jGa) × u(jGa))≤K.
Чтобы обеспечить конкурентное сокращение, после которого численность выживших особей будет пропорциональна их конкурентоспособности, используется следующая процедура.
1. На основании прошлогодней численности и выживаемости особей вычисляется «входная» численность всех групп: w(jGa)t = n(jGa-1)t-1× s(jGa).
2. Вычисляется потребность в ресурсах особей всех генотипов: Ot = Σ(w(jGa)t × u(jGa)).
3. Если Ot ≤ K (то есть ресурсов для всех достаточно), тогда для всех групп n(jGa)t = w(jGa)t . В противном случае вычисления продолжаются.
4. Если Ot > K, то есть ресурсов для всех выживших недостаточно, происходит конкурентное сокращение их численности. Для этого вычисляется нормированная по конкурентоспособности численность всех групп: q(jGa)t = w(jGa)t × c(jGa)).
Итак, сокращение «входящего» количества особей до нормированного пропорционально их конкурентоспособности. После того, как такое сокращение произведено, численность всех групп особей должна изменяться в одно и то же количество раз. Чтобы определить его, следует вычислить количество ресурсов, которое требуется нормированным группам особей: Yt = Σ(q(jGa)t × u(jGa)).
5. Если Yt = K, то n(jGa)t = q(jGa)t. Если Yt > K, то окончательный расчет всех n(jGa)t проводится в соответствии с 6-м шагом алгоритма, а если Yt < K – с 7-м шагом.
6. Если Yt > K, снижение численности каждой из групп, пропорциональное их конкурентоспособности, не является окончательным, и откорректированная численность все равно слишком высока. Ее последующее снижение должно проводиться в равной степени для каждой из групп, причем уровень сокращения должен определяться отношением K и Yt : n(jGa)t = q(jGa)t × K/Yt.
7. Если Yt < K, пропорциональное конкурентоспособности сокращение численности каждой из групп не должно доходить до конца. От «входного» количества представителей каждой группы w(jGa)t нужно отнять определенную часть, пропорциональную разности между «входным» и нормированным по конкурентоспособности количествами. Поскольку (w(jGa)t - n(jGa)t)/(w(jGa)t - q(jGa)t) = (Ot - K) / (Ot - Yt), n(jGa)t = w(jGa)t - (w(jGa)t - q(jGa)t) × (Ot - K) / (K - Yt).
Проверкой правильности выполненных расчетов может стать вычисление количества ресурсов, требуемого после всех сокращений численности: Vt = Σ(n(jGa)t × u(jGa)). Если Vt = K, то сокращение проведено правильно.
Алгоритм образования пар при размножении
Лимитировать размножение особей и определять количество состоявшихся амплексусов X может количество потенциальных амплексусов как самок (FemalesH), так и самцов (MalesH). Обозначим как FemalesG генотипы, которые приводят к развитию самок, а MalesG – генотипы самцов. ТогдаFemalesHt = Σ(FemalesGa)t для всехa > m(FemalesGa). Следует учесть, что некоторые из самцов могут быть способны участвовать более чем в одном амплексусе, и поэтомуMalesh(MalesGa)t = n(MalesGa)t × (1 + p(MalesGa)) иMalesHt = Σ(Malesh(MalesGa)t) для всехa > m(MalesGa). Если FemalesHt ≤ MalesHt (что более вероятно при относительном равенстве численности полов), то Xt = FemalesHt . Если же FemalesHt > MalesHt , то Xt = MalesHt .
В соответствии с принятыми при создании модели допущениями, в размножении принимают участие все особи «недостающего» пола и соответствующее количество особей «избыточного». Шансы на участие в амплексусах представителей избыточного пола должны быть пропорциональны их вероятности размножения R (см. табл. 2), и принятая в модели процедура сокращения их участия в размножении аналогична таковой для конкурентного исключения (см. выше).
Рассмотрим более вероятную ситуацию нормированного по вероятности размножения сокращения количества самцов, участвующих в размножении. Обозначим их нормированную численность в каждой группе как Malesz( MalesGa), а общее количество самцов в ГПС после нормированного сокращения – как MalesZ. Тогда для каждого генотипа можно указать, что Malesz( MalesGa) = n( MalesGa) × r( MalesGa) и MalesZt = Σ( Malesz(MalesGa)t).
Если MalesZt = X, то Malesx( MalesGa)t, количество самцов каждой группы, действительно участвующих в амплексусах, определяется по нормированной величине: Malesx( MalesGa)t = Malesz( MalesGa)t.
ЕслиMalesZt > X, тоMalesx(MalesGa)t = Malesz( MalesGa)t × ((Xt) / (MalesZt).
ЕслиMalesZt < X, тоMalesx(MalesGa)t = Malesh( MalesGa)t - (Malesh( MalesGa)t - Malesz( MalesGa)t) × (MalesHt - Xt) / (MalesHt - MalesZt).
При избытке самок сокращение количества их представителей, действительно участвующих в амплексусах, происходит в ходе аналогичной процедуры.
Когда установлен состав особей-производителей FemalesXt и MalesXt , можно определить состав пар в амплексусах. В описываемой модели принято, что все участвующие в размножении самки образуют пары со всеми участвующими в размножении самцами пропорционально численности групп самок и групп самцов. Количество амплексусов между представителями групп Females_1Ga и Males_1Ga определяется как произведение их численностей и их долей среди всех особей каждого пола:
X(Females_1Ga; Males_1Ga)t = Femalesx(Females_1Ga)t × (Femalesx(Females_1Ga)t) / (FemalesXt) × Malesx(Males_1Ga)t × (Xt) / (MalesZt) × (Malesx(Males_1Ga)t) / (MalesXt) .
Состав потомков при различных скрещиваниях
До настоящего места наше описание модели никак не касалось специфики гемиклонального наследования, характерного для межвидовых гибридов лягушек. Оно проявляется при образовании половых клеток, определяющих состав потомков, появляющихся в результате скрещиваний.
Не для всех вариантов скрещивания между зелеными лягушками установлено, какие гаметы будут производить образующиеся потомки. Именно для проверки предположений, относящихся к этой проблеме, и может быть применена описываемая модель. Однако для того, чтобы модель начала функционировать, необходимо предусмотреть начальные предположения. Если они будут противоречить одни другим, это проявится в экспериментах с моделью и отразится в несоответствии динамики моделируемых систем и эмпирических данных. Значит, со временем эти предположения могут быть откорректированы в сторону их лучшего соответствия действительности.
В соответствии с принятыми предположениями, в ГПС зеленых лягушек передаются геномы L и R, принадлежащие двум видам,P. lessonae и P. ridibundus. Каждый из этих геномов может быть мужским или женским. Для зеленых лягушек характерен механизм определения пола XY-типа, характерный и для человека, но без заметных морфологических отличий между половыми хромосомами. Исходя из сказанного, следует предусмотреть наличие 8 типов геномов: XL, YL, (XL), (YL), XR, YR, (XR), (YR). В случае диплоидных организмов генотип самки состоит из двух женских геномов, а генотип самца – из одного женского и одного мужского. В соответствии со сказанным, можно предположить существование 13 диплоидных генотипов: ♀♀XRXR, ♂♂XRYR, ♀♀(XL)XR, ♂♂(XL)YR, ♂♂(YL)XR, ♀♀XL(XR), ♂♂YL(XR), ♂♂XL(YR), ♀♀XLXL, ♂♂XLYL, ♀♀(XL)(XR), ♂♂(XL)(YR), ♂♂(YL)(XR). Из этих генотипов 5 принадлежат самкам, а 8 – самцам. Следовательно, между диплоидными лягушками возможно 5 × 8 = 40 типов скрещиваний. Добавление в рассмотрение триплоидных гибридов еще более увеличивает описанное разнообразие, однако в данной публикации мы не будем рассматривать ГПС, которые включают триплоидов.
В табл. 3 указаны генотипы, возникающие в различных скрещиваниях. Следует отметить, что многие ячейки этой таблицы заполнены достаточно произвольно. Например, при скрещиваниях P. lessonae и P. ridibundus, согласно табл. 3, возникающие гибриды должны передавать геном, полученный от матери. Однако так должно происходить не всегда. К примеру, в упомянутом выше Иськовом пруду был зарегистрирован период, когда все потомство от скрещивания самок P. ridibundus и самцов P. esculentus состояло из самцов P. esculentus (Шабанов и др., 2006). Такой результат возможен лишь в том случае, когда гибриды передают потомкам геном (YL). В то же время мужской геном не может быть получен гибридом от матери; значит, некоторые гибриды должны клонально передавать отцовский геном.
Таблица 3. Генотипы, возникающие при скрещивании различных диплоидных форм лягушек (одна из возможных версий)
|
Генотипы |
|
♀XRXR |
♀(XL)XR |
♀XL(XR) |
♀(XL)(XR) |
♀XLXL |
|
|
Гаметы |
XR |
(XL) |
(XR) |
(XL) : (XR) |
XL |
|
♂XRYR |
XR : YR |
XRXR : XRYR |
(XL)XR : (XL)YR |
XRXR : XRYR |
(XL)XR : (XL)YR : XRXR : XRYR |
(XL)XR : (XL)YR |
|
♂(XL)YR |
(XL) |
(XL)XR |
XLXL |
(XL)(XR) |
XLXL : (XL)(XR) |
XLXL |
|
♂(YL)XR |
(YL) |
(YL)XR |
XLYL |
(YL)(XR) |
XLYL : (YL)(XR) |
XLYL |
|
♂YL(XR) |
(XR) |
XRXR |
(XL)(XR) |
XRXR |
(XL)(XR) : XRXR |
XL(XR) |
|
♂XL(YR) |
(YR) |
XRYR |
(XL)(YR) |
XRYR |
(XL)(YR) : XRYR |
XL(YR) |
|
♂(XL)(YR) |
(XL) : (YR) |
(XL)XR : XRYR |
XLXL : (XL)(YR) |
(XL)(XR) : XRYR |
XLXL : (XL)(YR) : (XL)(XR) : XRYR |
XLXL : XL(YR) |
|
♂(YL)(XR) |
(YL) : (XR) |
(YL)XR : XRXR |
XLYL : (XL)(XR) |
(YL)(XR) : XRXR |
XLYL : (XL)(XR) : (YL)(XR) : XRXR |
XLYL : XL(XR) |
|
♂XLYL |
XL : YL |
XL(XR) : YL(XR) |
XLXL : XLYL |
XL(XR) : YL(XR) |
XLXL : XLYL : XL(XR) : YL(XR) |
XLXL : XLYL |
Еще одной проблемой, которая не имеет однозначного решения, является характер гаметогенеза у особей, получающих от родителей два генома, относящихся к одному виду, причем таких, что один или оба из этих геномов передавались как клональные. В табл. 3 показан вариант развития событий, при котором такие геномы вновь становятся рекомбинантными. Этот вариант также не является единственно возможным. Например, известен феномен, названный гибридолизом (Plötner, 2005). Он заключается в том, что особи от скрещиваний (L)R × (L)R → LL или L(R) × L(R) → RR, т.е. представители родительского вида, получившие два своих генома от родителей-гибридов, передававших его гемиклонально, обладают пониженной жизнеспособностью. В Северско-Донецком центре разнообразия зеленых лягушек отсутствуют взрослые представители P. lessonae, однако передаются клональные геномы этого вида (Шабанов, Литвинчук, 2010). Молодые особи P. lessonae здесь иногда возникают, но не доживают до половозрелости. Это, вероятнее всего, является следствием неблагоприятных эффектов гибридолиза. Отражать такого рода феномены в описываемой модели можно двояко. Первый вариант заключается в том, чтобы в соответствующей ячейке табл. 3 указать, что от такого скрещивания не возникает потомков. Второй вариант состоит в том, чтобы при моделировании процессов в Северско-Донецком центре разнообразия зеленых лягушек указать для P. lessonae критично низкие значения выживаемости (табл. 2).
Оставив обсуждение этих проблем для следующих публикаций, укажем, что по данным, приведенным в табл. 3, можно вычислить количество разных форм лягушек, ожидаемое в потомстве. Так, гибриды, которые были массово распространены в Иськовом пруду, возникают всего в двух типах скрещиваний: n(XR(YL)0) = X(XRXR; XR(YL)) + 0,5X(XRXR;(YL)(XR)).
Реализация модели на основе Microsoft Excel
Мы описали алгоритмы всех расчетов, выполняющихся в модели. На каждом шагу в ней выполняется моделирование следующих процессов:
– учет смертности в результате неполной выживаемости особей;
– прибавление иммигрантов (если они были указаны для данного шага особо);
– конкурентное сокращение численности (при необходимости);
– определение количества амплексусов и состава пар;
–вычисление количества появившегося потомства.
После выполнения этих операций модель переходит на следующий промежуток дискретного времени (год). Все указанные операции заданы разностными уравнениями, которые оперируют определенным набором исходно заданных параметров и результатами предшествовавших вычислений. Значит, эти вычисления можно проводить последовательно.
Вполне подходящую среду для реализации такой модели предоставляет программа Microsoft Office Excel (Коросов, 2002; Уокенбах, 2004). Авторами данной статьи создан файл Microsoft Excel, названный Batrachometrics‑2010 и содержащий следующие элементы:
– блок ячеек для указания параметров приспособленности всех рассматриваемых в модели форм лягушек (наподобие табл. 2 в данной статье), а также емкости среды – К;
– блок ячеек, в которых указываются результаты всех возможных скрещиваний;
– блок ячеек для указания начального состава ГПС;
– блоки строк, состоящие из ячеек, где с помощью заданных формул производится по отдельности для каждой группы особей весь комплекс вычислений, описанный в данной статье;
– сводные таблицы динамики разных форм лягушек с течением модельного времени;
– диаграмма для визуализации полученных результатов.
Описанная модель (в виде файла Batrachometrics‑2010.xls) находится в свободном интернет-доступе на сайте Центральной научной библиотеки ХНУ (https://dspace.univer.kharkov.ua/handle/123456789/2037).
Непростой проблемой, которая нуждается в своем решении при конструировании модели, является определение характера округления получаемых в ходе ее функционирования величин. Если все промежуточные величины (рассчитанные численности разных групп лягушек) округлять до целых величин, то формы, которые появляются с невысокой частотой, никогда не смогут проявиться, поскольку их численность будет закономерно округляться до нулевой. MSExcel позволяет проводить вычисления с очень высокой точностью (большим количеством знаков после запятой), рассматривая полученные результаты не как численности определенных групп особей (которые не могут быть нецелыми), а как величины их математического ожидания. Однако при такой организации вычислений те из форм особей, которые вытесняются из ГПС, в модели не могут уйти из нее до конца: в течение неопределенно длительного срока для них будет предусматриваться исчезающее малая, но положительная численность.
В реализованном варианте модели Batrachometrics‑2010 предусмотрено, что все расчеты проводятся с высокой точностью, но в размножении принимают участие только те формы лягушек, численность которых превышает 0,1. В качестве перспективы для дальнейших исследований можно рассмотреть вариант, при котором округление до целых чисел происходит случайно. Последовательно проводя исследования с одними и теми же начальными данными, при таком варианте можно получить определенное множество конечных состояний модели. Анализируя его, можно оценивать вероятность перехода моделируемой ГПС из одного состояния в другое.
Пример работы модели
В задачи данной статьи не входит подробный анализ работы модели и результатов ее применения. Тем не менее, приведем пример характерных особенностей ГПС, возникающих при реализации описанных алгоритмов. Рассматривается популяция P. ridibundus, обитающая в регионе, где все P. lessonae возникают в результате гибридолиза и поэтому нежизнеспособны. Попадание в такую популяцию гибридных особей, передающих конспецифичный геном (геном P. ridibundus), не приводит ни к каким долгосрочным последствиям. Клональный геном P. ridibundus, полученный от P. esculentus, «растворяется» в популяции P. ridibundus в результате рекомбинации. Иные последствия вызывает добавление в P. ridibundus особей, передающих гетероспецифичный геном, т.е. геном P. lessonae. При их скрещивании с особями родительского вида все потомство состоит из таких же гибридных особей: (L)R × RR → (L)R. Два других типа скрещиваний, происходящих в такой ГПС, таковы. При скрещивании особей родительского вида получаются особи того же вида (RR × RR → RR), а при скрещивании гибридов возникают нежизнеспособные особи: (L)R × (L)R → LL → †. По мере нарастания количества гибридов в ГПС ее способность к воспроизводству снижается до нуля (рис. 1).
Однако после того как в ГПС лягушек, развившихся на основе P. ridibundus, накапливается значительное количество особей, передающих гетероспецифичные геномы, эта ГПС оказывается благоприятной для особей P. esculentus, передающих конспецифичные геномы. Такая ГПС оказывается способной перейти в состояние устойчивого равновесия (рис. 2, рис. 3). На рис. 2 показана динамика нескольких различных форм лягушек. Более наглядной является траектория системы в фазовом пространстве, показывающем, какие именно геномы передаются в составе половых клеток в моделируемой ГПС (рис. 3). Этих геномов всего три: R, (L) и (R).
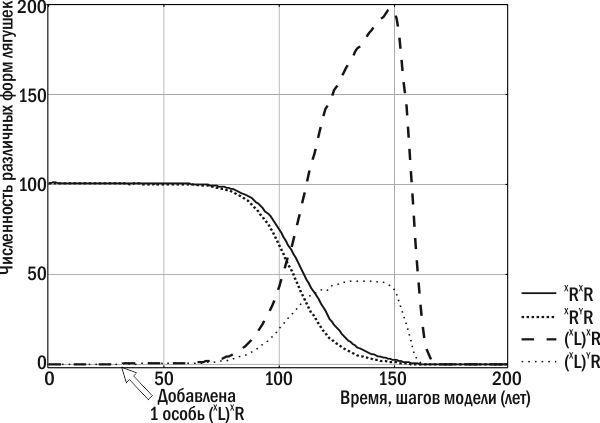
Рис. 1. Численность различных форм лягушек в составе нерестового стада в ходе эксперимента с моделью Batrachometrics‑2010. В популяцию P. ridibundus на 30-м году добавлена самка P. esculentus, которая передает гетероспецифичный клональный геном. Особи родительского вида вытесняются самками и самцами P. esculentus (самок в два раза больше), после чего ГПС прекращает существование
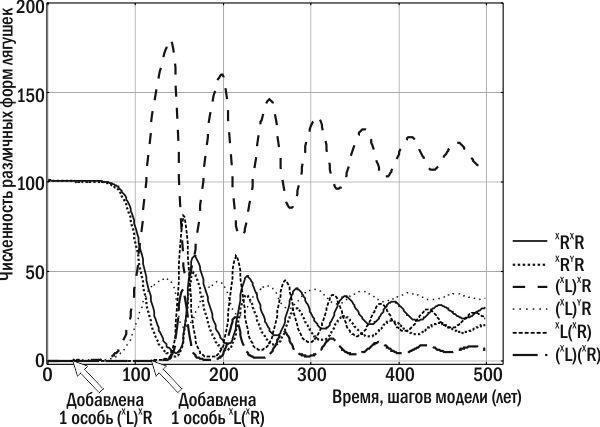
Рис. 2. Численность различных форм лягушек в составе нерестового стада в ходе эксперимента с моделью Batrachometrics‑2010. В популяцию P. ridibundus на 30‑м году имитации добавлена самка P. esculentus с гетероспецифичным клональным геномом, а на 120‑м году – самка P. esculentus, передающая конспецифичный клональный геном. ГПС в ходе колебания численности различных форм приближается к точке устойчивого равновесия
Представленные на рис. 1–3 результаты демонстрируют нетривиальные свойства систем, моделируемых с помощью Batrachometrics‑2010. Эти свойства не были заложены в модель явно. Сам по себе механизм конкурентного исключения и образования пар не приводит к сложной динамике систем и лишь благоприятствует более жизнеспособным формам. Показанная на рис. 1–3 динамика является, помимо прочего, следствием предусмотренной в показанных экспериментах нежизнеспособности особей P. lessonae, появившихся вследствие гибридолиза. Подчеркнем, что это предположение подтверждается при исследовании Северско-Донецкого центра разнообразия зеленых лягушек (Шабанов, Литвинчук, 2010). Кроме того, сложная динамика модели определяется характером потомства, возникающегов результате размножения (табл. 3).
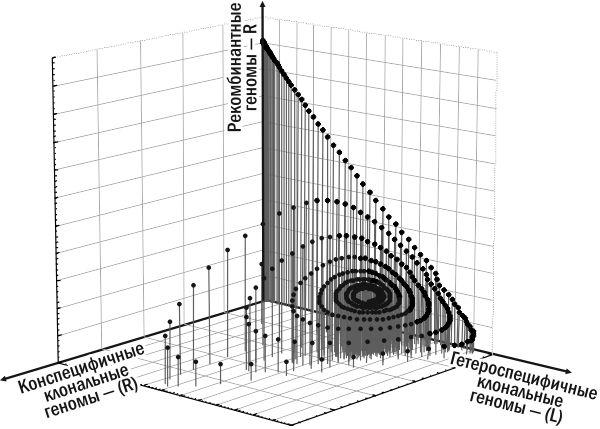
Рис. 3. Состав геномов, передающихся в половых клетках особей, составляющих ГПС лягушек эксперимента с моделью Batrachometrics‑2010. Показаны те же процессы, что и на рис. 2. Начальная точка –вверху, на оси ординат, соответствует популяции P. ridibundus. С 30‑го года начинает нарастать численность гетероспецифичных клональных геномов, а после 120‑го года – и конспецифичных клональных геномов. ГПС в рассматриваемом фазовом пространстве движется по сужающейся спиралеподобной траектории к точке-аттрактору, соответствующей устойчивому состоянию
Итак, результатом нашей работы является построение математической модели ГПС зеленых лягушек, позволяющей в широких пределах изменять положенные в основу ее функционирования предположения, и определять, как это скажется на свойствах системы в целом. Авторы надеются, что эта модель поможет в анализе имеющихся представлений и предположений о механизмах функционирования гемиклональных популяционных систем зеленых лягушек и будет способствовать расширению нашего понимания феномена гемиклонального наследования.
Благодарности
Модель, описанная в данной работе, появилась в результате обсуждений и исследований целой группы специалистов. Авторы искренне благодарны М.В.Владимировой, Г.Н.Жолткевичу, А.А.Луцику за неоценимую помощь в формализации задачи и за создание моделей ГПС зеленых лягушек, основанных на ином вычислительном принципе, чем тот, который описан в данной работе (Владимирова и др., 2007). Моделирование ГПС тесно связано с работой целой группы биологов, занятых изучением зеленых лягушек. В их числе А. В. Коршунов, Г .А. Мазепа, Е. Е. Усова. Неоценимую помощь эта группа получила от коллег из Санкт-Петербурга, в особенности – С. Н. Литвинчука, и Киева, прежде всего – С. Ю. Морозова-Леонова. Особую благодарность авторы выражают А. Г. Козленко, вместе с которым они получили первый опыт моделирования экологических систем средствами MS Excel.
Работа выполнена при поддержке совместного гранта ГФФИ Украины (проект 09-04-90475) и РФФИ (Россия).
Список литературы
Ананьева Н.Б., Боркин Л.Я., Даревский И.С., Орлов Н.Л. Земноводные и пресмыкающиеся. Энциклопедия природы России. – М.: ABF, 1998. – 576 с. / Ananyeva N.B., Borkin L.Ya., Darevskiy I.S., Orlov N.L. Zemnovodnyye i presmykayushchiyesya. Entsiklopediya prirody Rossii. – M.: ABF, 1998. – 576 s./
Бигон М., Харпер Дж., Таунсенд К. Экология. Особи, популяции и сообщества: в 2-х т. Т.1. –М.: Мир, 1989. –677 с. / Bigon M., Harper Dzh., Taunsend K. Ekologiya. Osobi, populyatsii i soobshchestva: v 2-kh t. T.1. – M.: Mir, 1989. – 677 s./
Боркин Л.Я., Зиненко А.И., Коршунов А.В. и др. Массовая полиплоидия в гибридогенном комплексе Rana esculenta (Ranidae, Anura, Amphibia) на Востоке Украины // Матеріали Першої конференції Українського Герпетологічного Товариства. – К.: Зоомузей ННПМ НАНУ, 2005. – С. 23–26. /BorkinL.Ya., ZinenkoA.I., KorshunovA.V. idr. Massovaya poliploidiya v gibridogennom komplekse Rana esculenta (Ranidae, Anura, Amphibia) naVostoke Ukrainy // Materіaly Pershoi konferentsіi Ukrains'kogo Gerpetologіchnogo Tovarystva. – K.: Zoomuzey NNPMNANU, 2005. – S. 23–26/
Владимирова М.В., Жолткевич Г.Н., Луцик А.А., Шабанов Д.А. Исследование целостных свойств биосистем на примере имитационного моделирования гибридогенных популяционных систем зеленых лягушек // Вісник Харківського національного університету. Серія «Математичне моделювання. Інформаційні технології. Автоматизовані системи управління». –2007. –№780. –C. 61–70. /Vladimirova M.V., Zholtkevich G.N., Lutsik A.A., Shabanov D.A. Issledovaniye tselostnykh svoystv biosistem na primere imitatsionnogo modelirovaniya gibridogennykh populyatsionnykh sistem zelenykh lyagushek// Vіsnyk Kharkіvs'kogo natsіonal'nogo unіversytetu. Serіya «Matematychne modelyuvannya. Іnformatsіynі tekhnologіi. Avtomatyzovanі systemy upravlіnnya». – 2007. – №780. – C. 61–70/
Коросов А.В. Имитационное моделирование в среде MS Excel (на примерах из экологии). – Петрозаводск: ПетрГу, 2002. – 212 с. / Korosov A.V. Imitatsionnoye modelirovaniye v srede MSExcel (na primerakh iz ekologii). – Petrozavodsk: PetrGu, 2002. – 212 s./
Коршунов А.В. Экологические особенности биотопического распределения представителей Pelophylax esculentus complex в Харьковской области // Вісник Харківського національного університету імені В.Н.Каразіна. Серія: біологія. – 2008. – Вип. 8 (№828). – С. 48–57. / Korshunov A.V. Ekologicheskiye osobennosti biotopicheskogo raspredeleniya predstaviteley Pelophylax esculentus complex v Khar'kovskoy oblasti // Vіsnyk Kharkіvs'kogo natsіonal'nogo unіversytetu іmenі V.N.Karazіna. Serіya: bіologіya. – 2008. – Vyp. 8 (№ 828). – S. 48–57/
Ризниченко Г.Ю. Математические модели в биофизике и экологии. – Москва–Ижевск: Институт компьютерных исследований, 2003. – 184 с. / Riznichenko G. Yu. Matematicheskiye modeli v biofizike i ekologii. – Moskva–Izhevsk: Institut kompyuternykh issledovaniy, 2003. – 184 s.
Смирина Э.М. Прижизненное определение возраста и ретроспективная оценка размеров тела серой жабы (Bufo bufo) // Зоол. журн. – 1983. – Т.63, №3. – С. 437–444. /Smirina E.M. Prizhiznennoye opredeleniye vozrasta i retrospektivnaya otsenka razmerov tela seroy zhaby (Bufo bufo) // Zool. zhurn. – 1983. – T.63, №3. – S. 437–444/
Уокенбах Дж. Excel 2003. Библия пользователя. – М.: Издательский дом «Вильямс», 2004. – 768 с. /Uokenbah Dzh. Excel 2003. Bibliya pol'zovatelya. – M.: Izdatel'skiy dom «Vilyams», 2004. – 768 s./
Усова Е.Е. Возрастная структура представителей гибридогенного комплекса зеленых лягушек в Харьковской области // Мат. ХI Междунар. научно-практич. экол. конф. – Белгород, 2010. – С. 131. /UsovaYe.Ye. Vozrastnaya struktura predstaviteley gibridogennogo kompleks azelenykh lyagushek v Khar'kovskoy oblasti// Mat. XI Mezhdunar. nauchno-praktich. ekol. konf. – Belgorod, 2010. – S. 131/
Шабанов Д.А., Зиненко А.И., Коршунов А.В. и др. Изучение популяционных систем зеленых лягушек (Rana esculenta complex) в Харьковской области: история, современное состояние и перспективы // Вісник Харківського національного університету імені В.Н.Каразіна. Серія: біологія. –2006. –Вип.3 (№729). –С. 208–220./Shabanov D.A., Zinenko A.I., Korshunov A.V. i dr. Izucheniye populyatsionnykh sistem zelenykh lyagushek (Rana esculenta complex) v Khar'kovskoy oblasti: istoriya, sovremennoye sostoyaniye i perspektivy // Vіsnyk Kharkіvs'kogo natsіonal'nogo unіversytetu іmenі V.N.Karazіna. Serіya: bіologіya. – 2006. – Vyp.3 (№729). – S. 208–220/
Шабанов Д.А., Кравченко М.А. Материалы для изучения курса общей экологии с основами средоведения и экологии человека. – Х.: ХНУ имени В.Н.Каразина, 2009. – 292 с. / Shabanov D.A., Kravchenko M.A. Materialy dlya izucheniya kursa obshchey ekologii s osnovami sredovedeniya iekologii cheloveka. – H.: HNUimeniV.N.Karazina, 2009. – 292 s./
Шабанов Д.А., Коршунов О.В., Кравченко М.О. Які ж зелені жаби населяють Харківську область? Термінологічний і номенклатурний аспекти проблеми // Біологія та валеологія. – Харків: ХДПУ, 2009. – Вип.11. – С. 164–125. /Shabanov D.A., Korshunov O.V., Kravchenko M.O. Yakі zhzelenі zhaby naselyayut' Kharkіvs'ku oblast'? Termіnologіchnyyі nomenklaturnyy aspekty problemy// Bіologіya ta valeologіya. – Harkіv: HDPU, 2009. – Vyp.11. – S. 164–125/
Шабанов Д.А., Литвинчук С.Н. Зеленые лягушки: жизнь без правил или особый способ эволюции? // Природа. – 2010. – №3. – С. 29–36./Shabanov D.A., Litvinchuk S.N. Zelenyye lyagushki: zhizn' bez pravil ili osobyy sposob evolyutsii? // Priroda. – 2010. – №3. – S. 29–36/
Шалдыбин С.Л. Возрастная и половая структура популяций бесхвостых амфибий // Природные ресурсы Волжско–Камского края. Животный мир. Вып.4. – Казань, 1976. – С. 112–117. / Shaldybin S.L. Vozrastnaya i polovaya struktura populyatsiy beskhvostykh amfibiy// Prirodnyye resursy Volzhsko–Kamskogo kraya. Zhivotnyymir. Vyp.4. – Kazan', 1976. – S. 112–117/
Borkin L.J., Korshunov A.V., Lada G.A. etal. Mass occurrence of polyploid green frogs (Rana esculenta complex) in Eastern Ukraine // Russian Journal of Herpetology. – 2004. – Vol.11, №3. –P. 194–213.
Frost D.R., Grant T., Faivovich J.N. et al. The Amphibian tree of life. – Bull. Amer. Mus. Nat. Hist. – 2006. – №297. – 370 p.
Plötner J. Die westpaläarktichen Wasserfrösche. – Bielefeld: Laurenti-Verlag, 2005. – 161 S.
Представлено: С. М. Литвинчуком / Presented by: S. N. Litvinchuk
Рекомендовано до друку: Є. Е. Перським / Recommended for publishing by: Ye. E. Persky
Подано до редакції /Received: 28.10.2010.
Коментарі
Что это за пустые рамочки
в тексте? Тут и так попотеть придётся, чтоб осознать, а тут ещё они.
А, ещё в заглавном тесте какие-то формулИ наочепятались.
[по прочтении удалить]
А поподробнее можно?
У меня отображается нормально. Можно отправить скрин (например, сделанный через PrtSc) на мое мыло?
Отправлено.
На d.a.shabanov@gmail.com, верно?
Спасибо
Да, это было серьезно... А сейчас исчезло? Я вынужден был убирать "вслепую", и где-то могло остаться...
Осталось местами:
1. после Таблица 2. Комплекс параметров жизнеспособности, задаваемых в модели для каждого генотипа (на примере генотипа jG
2. после Так, гибриды, которые были массово распространены в Иськовом пруду, возникают всего в двух типах скрещиваний:
также ссылка http://dspace.univer.kharkov.ua/handle/123456789/2037 ведёт в никуда
Большая же часть благополучно исчезла.
Указанные ошибки исправил
за исключением ссылки: дело в том, что университетский репозиторий почему-то вообще сейчас "молчит".